算法学习->归并排序

nwpu-2020级算法实验1-problemB

Overview

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

有两种实现方式：

• 自上而下的递归

  • 所有的递归都可以由迭代重写。

• 自下而上的迭代

算法步骤

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；

3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

4. 重复步骤 3 直到某一指针达到序列尾；

5. 将另一序列剩下的所有元素直接复制到合并序列尾。

其实就是leetcode中我做过的暴力合并数组

链接：4. 寻找两个正序数组的中位数 - 力扣（LeetCode） (leetcode-cn.com)

直观演示

算法分析

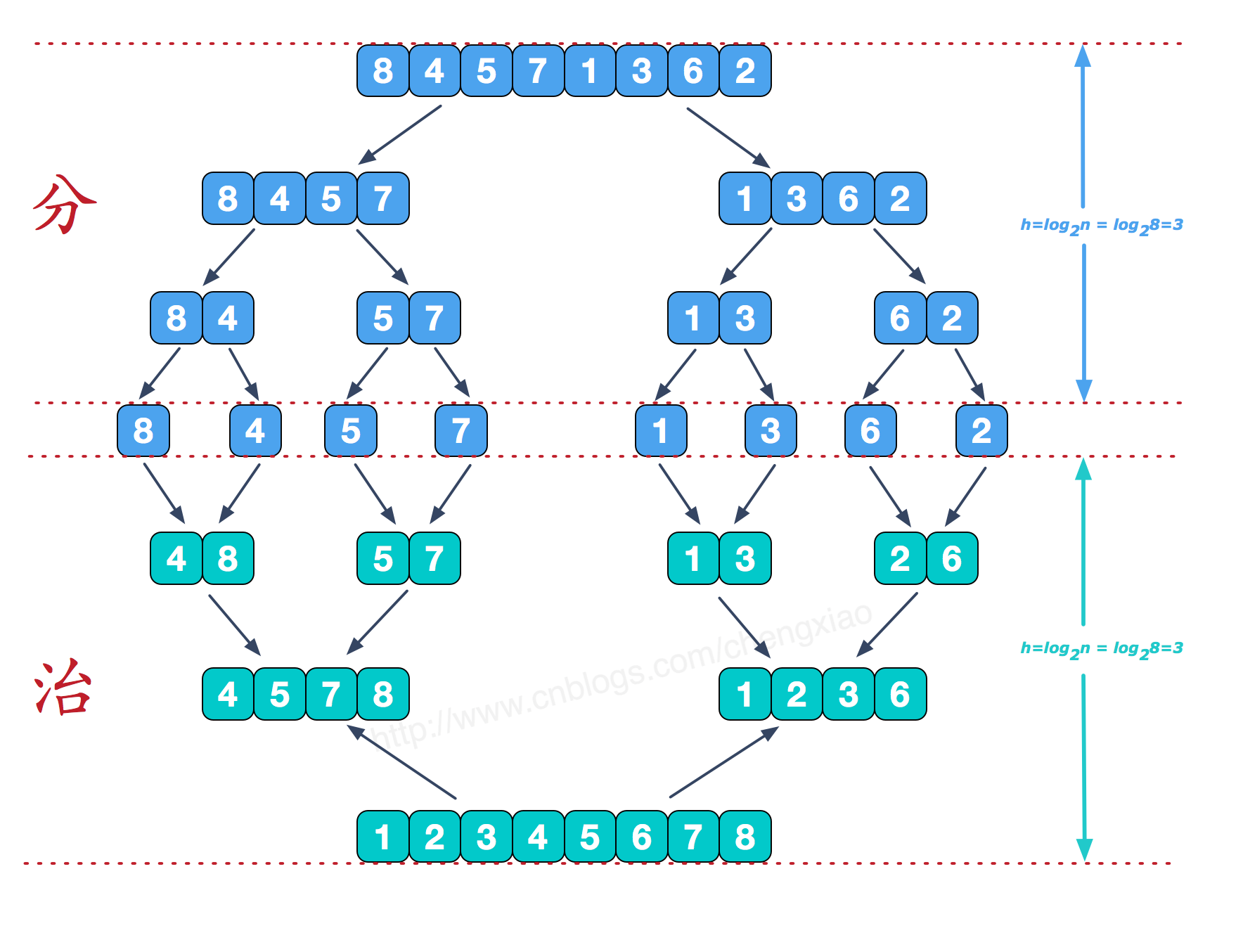
动图展示了我们实现算法的过程，而这个分治图静态展示了递归的流程。

分：递归拆分子序列，递归深度易得logn

治：将有序子序列合并为更大的有序序列。

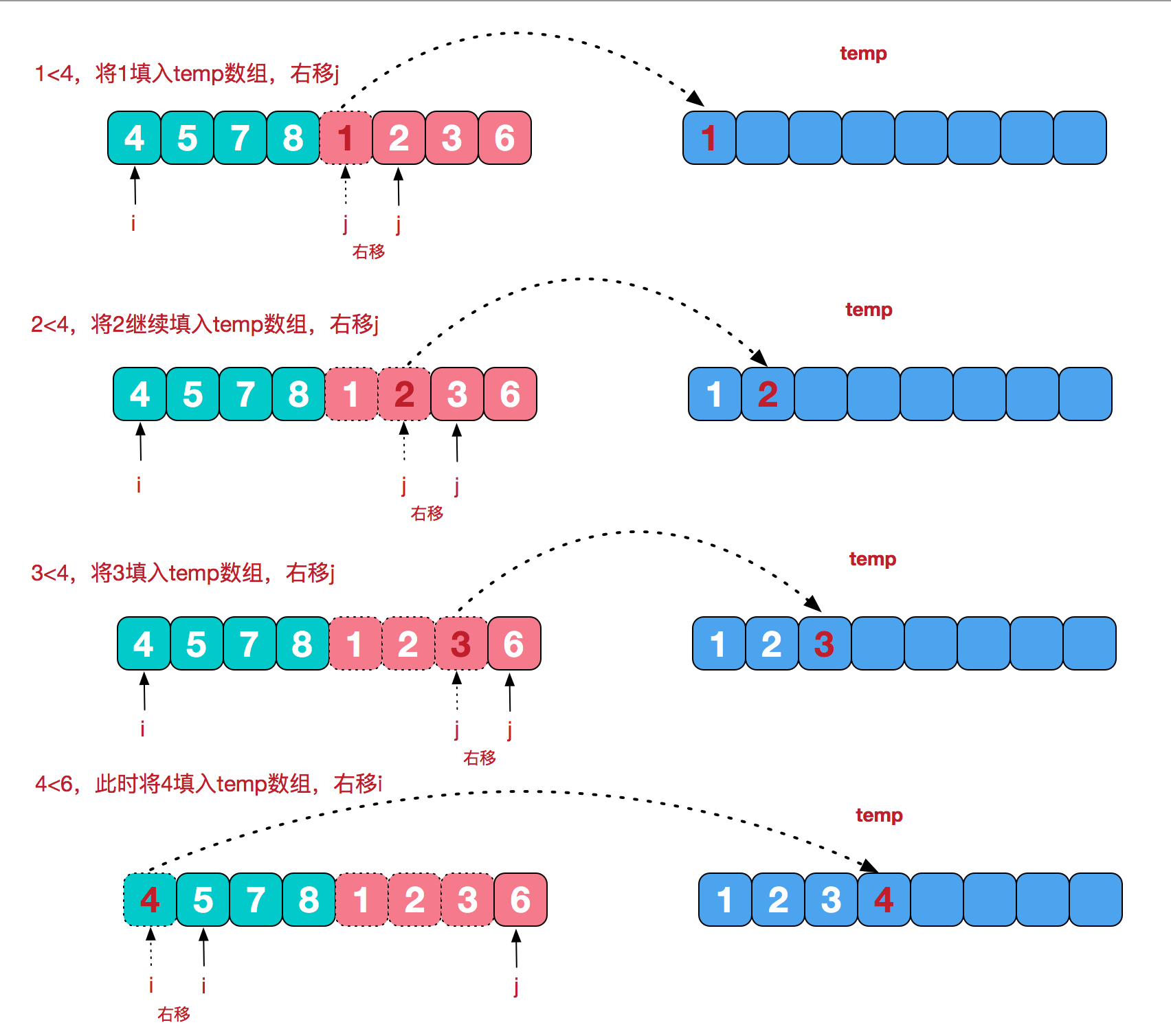
下面是治的最后一步的过程（熟练可略过）：

算法实现

C递归

 1 //归并排序递归
 2 #include<stdio.h>
 3 //#include<stdlib.h>
 4 //#include<iostream>
 5 using namespace std;
 6 void merge_sort_recursive(int arr[], int reg[], int start, int end) {
 7     if (start >= end)
 8         return;
 9     //停止递归的条件，即只有单个元素时必定有序
10     int len = end - start, mid = (len >> 1) + start;
11     int start1 = start, end1 = mid;//第一个数组
12     int start2 = mid + 1, end2 = end;//第二个数组
13     merge_sort_recursive(arr, reg, start1, end1);
14     merge_sort_recursive(arr, reg, start2, end2);
15     //将数组拆分，直到上面的if生效(即每个子序列只有单个元素)，此时停止递归，开始回溯
16     int k = start;
17     while (start1 <= end1 && start2 <= end2)
18         reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
19     //这种写法更为简洁，实现的就是谁小谁放进去
20     while (start1 <= end1)
21         reg[k++] = arr[start1++];
22     while (start2 <= end2)
23         reg[k++] = arr[start2++];
24     //多余元素直接放入reg
25     for (k = start; k <= end; k++)
26         arr[k] = reg[k];
27     //一次返回赋值，即把reg里排好序的元素粘回arr
28 }
29 ​
30 void merge_sort(int arr[], const int len) {
31     int reg[len];//构造算法步骤中所说的新的数组
32     merge_sort_recursive(arr, reg, 0, len - 1);
33     //启动递归
34     //输出
35     for(int i = 0; i < len; i++){
36         printf("%d\n", arr[i]);
37     }
38     //此处还可以clear *reg来保证代码安全。
39 }
40 int main(){
41     int n;
42     scanf("%d", &n);
43     int Array[n];
44     for(int i = 0; i < n; i++){
45         scanf("%d", &Array[i]);
46     }
47     merge_sort(Array, n);
48     return 0;
49 }

参考文章：

1.5 归并排序 | 菜鸟教程 (runoob.com)