Proximal Algorithms 4 Algorithms

Proximal minimization
- 解释
  - Gradient flow
加速 proximal gradient method
交替方向方法 ADMM

Proximal Algorithms

这一节介绍了一些利用proximal的算法.

Proximal minimization

这个相当的简单, 之前也提过，就是一个依赖不动点的迭代方法:

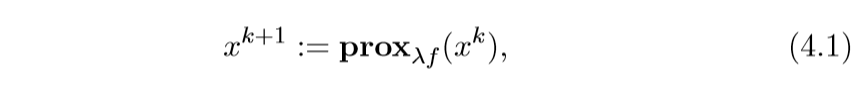
有些时候$\lambda$不是固定的:

\[x^{k+1} := \mathbf{prox}_{\lambda^k f}(x^k), \sum_{k=1}^{\infty}\lambda^k = \infty
\]

import numpy as np

import matplotlib.pyplot as plt

以$f(x,y) = x^2 + 50y$为例

f = lambda x: x[0] ** 2 + 50 * x[1] ** 2

x = np.linspace(-40, 40, 1000)

y = np.linspace(-20, 20, 500)

X, Y = np.meshgrid(x, y) #获取坐标

fig, ax = plt.subplots()

ax.contour(X, Y, f([X, Y]), colors="black")

plt.show()

求解proximal可得:

\[x = \frac{v_1}{2\lambda + 1} \\
y = \frac{v_2}{100\lambda + 1}
\]

def prox(v1, v2, lam):

    x = v1 / (2 * lam + 1)

    y = v2 / (100 * lam + 1)

    return x, y

times = 50

x = 30

y = 15

lam = 0.1

process = [(x, y)]

for i in range(times):

    x, y = prox(x, y, 0.1)

    process.append((x, y))

process = np.array(process)

x = np.linspace(-40, 40, 1000)

y = np.linspace(-20, 20, 500)

X, Y = np.meshgrid(x, y) #获取坐标

fig, ax = plt.subplots()

ax.contour(X, Y, f([X, Y]), colors="black")

ax.scatter(process[:, 0], process[:, 1])

ax.plot(process[:, 0], process[:, 1])

plt.show()

解释

除了之前已经提到过的一些解释：

Gradient flow

考虑下面的微分方程:

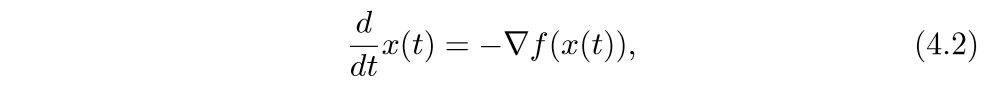
$t \rightarrow \infty$时$f(x(t))\rightarrow p^*$，其中$p^*$是最小值.

我们来看其离散的情形:

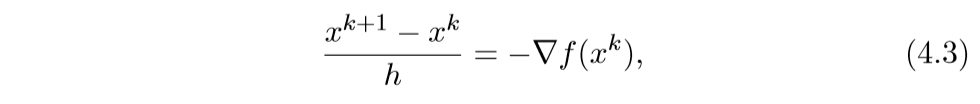
于是就有：

\[x^{k+1} := x^k - h \nabla f(x^k)
\]

还有一种后退的形式:

\[\frac{x^{k+1}-x^k}{h}=-\nabla f(x^{k+1})
\]

此时，为了找到$x^{k+1}$, 我们需要求解一个方程:

\[x^{k+1} + h \nabla f(x^{k+1}) = x^k \\
\Rightarrow x^{k+1} = (I+ h \nabla f)^{-1}x^k = \mathbf{prox}_{hf}(x^k)
\]

还有一种特殊的解释，这里不提了.

$f(x) + g(x)$

考虑下面的问题:

\[\mathrm{minimize} \quad f(x) + g(x)
\]

其中$f$是可微的.

我们可以通过下列proximal gradient method来求解:

\[x^{k+1} := \mathbf{prox}_{\lambda^k g}(x^k - \lambda^k \nabla f(x^k))
\]

可以证明(虽然我不会)，当$\nabla f$ Lipschitz连续，常数为$L$，那么，如果$\lambda^k = \lambda \in (0, 1/L]$，这个方法会以$O(1/k)$的速度收敛.

还有一些直线搜素算法:

一般取$\beta=1/2$，$\widehat{f}_{\lambda}$是$f$的一个上界，在后面的解释中在具体探讨.

解释1 最大最小算法

最大最小算法，最小化函数$\varphi: \mathbb{R}^n \rightarrow \mathbb{R}$:

\[x^{k+1} := \mathrm{argmin}_x \widehat{\varphi}(x, x^k)
\]

其中$\widehat{\varphi}(\cdot, x^k)$是$\varphi$的凸上界:$\widehat{\varphi}(x, x^k) \ge \varphi(x)$, $\widehat{\varphi}(x, x)=\varphi(x)$.

我们可以这么构造一个上界:

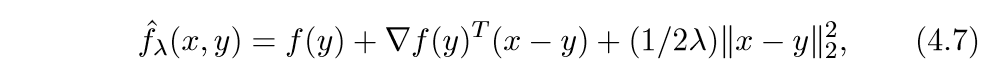
上面的式子很像泰勒二阶展开，首先这个函数符合第二个条件，下面我们证明，当$\lambda \in (0, 1/L]$，那么它也符合第一个条件.

\[\widehat{f}_{\lambda}(x) - f(x) = f(y) - f(x) +\nabla f(y)^T(x-y)+...=(\nabla f(y)-\nabla f(z))(x-y)+...
\]

其中$z = x + \theta (y-x), \theta \in [0, 1]$, 又Lipschitz连续，所以:

\[\|\nabla f(y)-\nabla f(z)\| \le L\|y-z\|\le L\|y-x\|
\]

考虑$f(x+t\Delta x)$关于$t$的二阶泰勒展式:

\[f(x+t\Delta x) = f(x)+\nabla f(x)^T\Delta x t + \frac{1}{2}\Delta x^T \nabla^2f(x) \Delta x t^2 + o(t^2)
\]

令$t=1$:

\[f(x+\Delta x) = f(x)+\nabla f(x)^T\Delta x + \frac{1}{2}\Delta x^T \nabla^2f(x) \Delta x + ...
\]

\[\frac{\|\nabla f(x)-\nabla f(x+t\Delta x)\|}{t}\le L\|\Delta x\|
\]

由当$t \rightarrow 0$时，左边为$\|\nabla^2 f(x) \Delta x\|$, 所以$\nabla^2 f(x)$的最大特征值必小于$L$, 所以:

\[f(x+\Delta x) \le f(x)+\nabla f(x)^T\Delta x + \frac{L}{2}\|\Delta x\|_2^2 + ...
\]

完蛋，好像只能证明在局部成立，能证明在全局成立吗？

\[x^{k+1} := \mathrm{argmin}_x \widehat{f}_{\lambda}(x, x^k)
\]

再令：

\[q_{\lambda}(x, y)=\widehat{f}_{\lambda}(x,y) + g(x)
\]

那么:

\[x^{k+1} := \mathrm{argmin}_x q_{\lambda}(x, x^k)=\mathbf{prox}_{\lambda g}(x^k-\lambda \nabla f(x^k))
\]

上面的等式，可以利用第二节中的性质推出.

不动点解释

最小化$f(x)+g(x)$的点$x^*$应当满足:

\[0 \in \nabla f(x^*)+\partial g(x^*)
\]

更一般地:

这便说明了一种迭代方式.

Forward-backward 迭代解释

考虑下列微分方程系统:

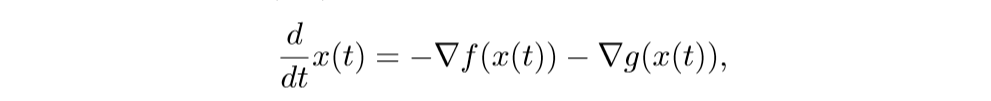
离散化后得:

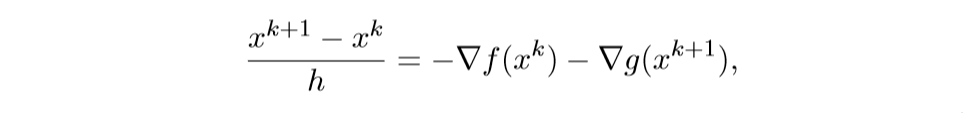
注意，等式右边$x^k$和$x^{k+1}$，这正是巧妙之处.

解此方程可得:

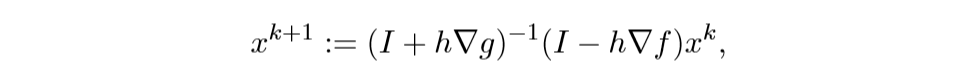
这就是之前的那个迭代方法.

加速 proximal gradient method

其迭代方式为:

\[y^{k+1} := x^k + w^k(x^k-x^{k-1}) \\
x^{k+1} := \mathbf{prox}_{\lambda^k g}(y^{k+1}-\lambda^k \nabla f(y^{k+1}))
\]

$w^k \in [0,1)$

这个方法有点类似Momentum的感觉.

一个选择是:

\[w^k = \frac{k}{k+3}
\]

也有类似的直线搜索算法:

交替方向方法 ADMM

alternating direction method of multipliers (ADMM), 怎么说呢，久闻大名，不过还没看过类似的文章.

同样是考虑这个问题:

\[\mathrm{minimize} \quad f(x) + g(x)
\]

但是呢，这时$f,g$都不一定是可微的, ADMM采取的策略是:

\[x^{k+1} := \mathbf{prox}_{\lambda f} (z^k - u^k) \\
z^{k+1} := \mathbf{prox}_{\lambda g} (x^{k+1} + u^k)\\
u^{k+1} := u^k + x^{k+1} -z^{k+1}
\]

特殊的情况是, $f$或$g$是指示函数，不妨设$f$是闭凸集$\mathcal{C}$的指示函数，而$g$是闭凸集$\mathcal{D}$的指示函数, 即:

\[I_{\mathcal{C}}(x)=0, if \: x\in \mathcal{C}, else \: + \infty
\]

这个时候，更新公式变为:

\[x^{k+1} := \Pi_{\mathcal{C}} (z^k - u^k)\\
z^{k+1} := \Pi_{\mathcal{C}} (x^{k+1} + u^k) \\
u^{k+1} := u^k + x^{k+1} -z^{k+1}
\]

解释1 自动控制

可以这么理解，$z$为状态，而$u$为控制，前俩步时离散时间动态系统(不懂啊...)，第三步的目标是选择$u$使得$x=z$，所以$x^{k+1}-z^{k+1}$可以认为是一个信号误差，所以第三步就会把这些误差累计起来.

解释2 Augmented Largranians

我们可以将问题转化为:

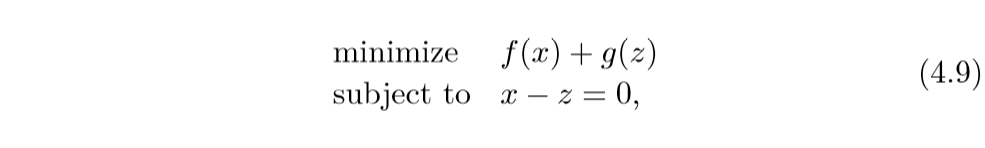
augmented Largranian:

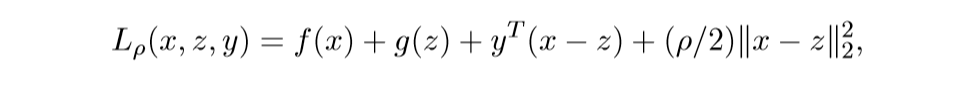
其中$y$为对偶变量.

在$z, y$已知的条件下，最小化$L$, 即:

\[x^{k+1} := \mathrm{argmin}_x L_{\rho}(x, z^k, y^k)
\]

在$x, y$已知的条件下，最小化$L$, 即:

\[z^{k+1} := \mathrm{argmin}_z L_{\rho}(x^{k+1}, z, y^k)
\]

最后一步:

\[y^{k+1} := y^k + \rho (x^{k+1} - z^{k+1}）
\]

如果依照对偶问题的知识，关于$y$应该是取最大，但是呢，关于$y$是一个仿射函数，所以没有最值，所以就简单地取那个？

注意到：

让$u^k = (1/\rho)y^k$, $\lambda = 1/\rho$就是最开始的结果.

解释3 Flow interpretation

问题(4.9)的最优条件(KKT条件):

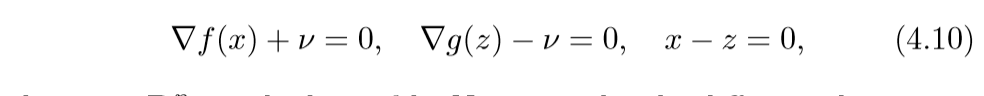
其中$v$是对偶变量.考虑微分方程：

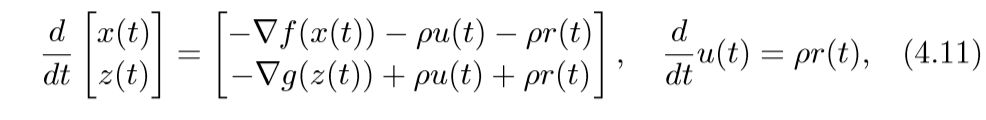
(4.11)取得稳定点的条件即为(4.10)($v=\rho)$(这部分没怎么弄明白).

离散化情形为:

取$h = \lambda, \rho = 1/\lambda$即可得ADMM.

解释4 不动点

原问题的最优条件为:

\[0 \in \partial f(x^*) + \partial g(x^*)
\]

ADMM的不动点满足：

\[x = \mathbf{prox}_{\lambda f} (x-u), \quad z = \mathbf{prox}_{\lambda g}(x+u), \quad u = u + x - z
\]

从最后一个等式，我们可以知道:

\[x = z
\]

, 于是

\[x = \mathbf{prox}_{\lambda f}(x - u), \quad x = \mathbf{prox}_{\lambda g}(x + u)
\]

等价于:

\[x = (I + \partial f)^{-1}(x - u), x = (I + \lambda \partial g)^{-1}(x + u)
\]

等价于:

\[x - u \in x + \lambda \partial f(x), \quad x + u \in x + \lambda \partial g(x)
\]

俩个式子相加，说明$x$即为最优解.

再来说明一下，为什么可以相加，根据次梯度的定义:

\[\lambda f(z) \ge \lambda f(x) + (-u)^T(z-x), \quad \forall z\in \mathbf{dom}f \\
\lambda g(z) \ge \lambda g(x) + (+u)^T(z-x), \quad \forall z\in \mathbf{dom}g \\
\]

相加可得:

\[\lambda f(z) + \lambda g(z) \ge 2x + \lambda f(x) +\lambda g(x) + 0
\]

需要注意的是，我证明的时候也困扰了，

\[x - u \in x + \lambda \partial f(x)
\]

并不是指(x-u)是函数$x^2/2 + \lambda f(x)$的次梯度, 而是$x-u$在$\lambda f(x)$的次梯度集合加上$x$的集合内，也就是$-u$是其次梯度.

对不起！又想当然了，其实没问题, 如果

\[g \in \partial f_1(x) + h(x)
\]

而$\partial f_2(x)=h(x)$则:

\[g \in \partial (f_1+f_2)(x)
\]

证:

已知:

\[f_1(z) \ge f_1(x)+\partial f_1(x)^T(z-x) \\
f_2(z) \ge f_2(x)+h(x)^T(z-x) \\
\]

俩式相加可得:

\[(f_1+f_2)(z)\ge (f_1+f_2)(x) +(\partial f_1(x) + h(x))^T(z-x)=(f_1+f_2)(x) +g^T(z-x)
\]

所以$g \in \partial (f_1+f_2)(x)$, 注意$g=g(x)$也是无妨的.

特别的情况 $f(x) + g(Ax)$

考虑下面的问题：

\[\mathrm{minimize} \quad f(x) + g(Ax)
\]

上面的求解，也可以让$\widetilde{g}(x) = g(Ax)$，这样子就可以用普通的ADMM来求解了, 但是有更加简便的方法.

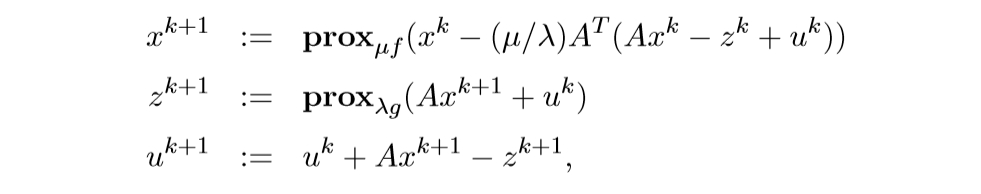
这个的来源为：

再利用和之前一样的推导，不过，我要存疑的一点是最后的替代，我觉得应该是:

\[\rho (A^TAx^k - A^T z^k)^T x + (1 / 2\mu) \|x-x^k\|_2^2
\]

否则推不出来啊.