[WPF] 使用三种方式实现弧形进度条

1. 需求

前天看到有人问弧形进度条怎么做，我模仿了一下，成果如下图所示：

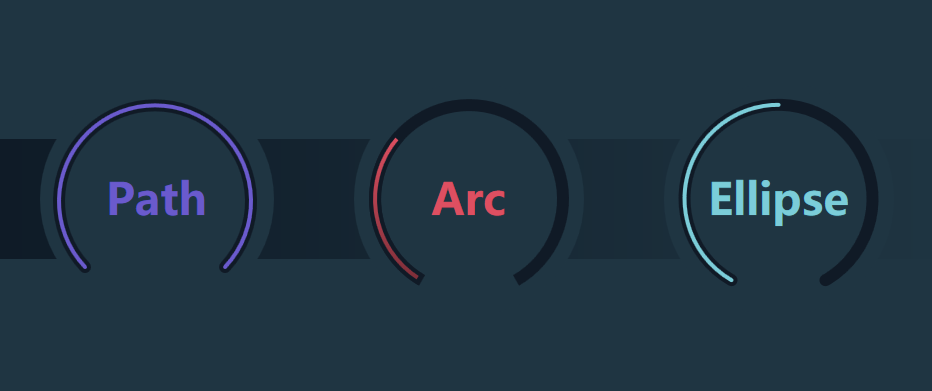
当时我第一反应是可以用 Microsoft.Toolkit.Uwp.UI.Controls 里的 RadialGauge 实现，虽然这是个 UWP 的控件，不过代码没有很复杂，应该很轻松就能移植到 WPF：

但仔细想想，我实现过很多次圆形的进度条，这种弧形的进度条则没碰过。原型进度条基本只需要用 Ellipse 就能实现，而且只需要 Progress 一个参数，而弧形进度条则还需要 StartAngle 和 EndAngle 两个属性，而且计算复杂许多。于是兴致来了试试用不同的方式实现弧形进度条。

这篇文章只介绍了怎么显示弧形及怎么显示进度，只有原理，没有具体实现一个弧形进度条控件。

2. 使用 Path 及 ArcSegment

Path 用于绘制曲线和复杂形状，而且 ArcSegment 用于描述 Path 中两点之间的一条椭圆弧。通常使用以下几个属性控制 ArcSegment：

属性	描述
Point	终点（起始点在 Path 或前一个 Segment 中描述）。
Size	X 轴和 Y 轴的半径。
IsLargeArc	圆弧是整个圆形中大的那部分，还是小的那部分。
SweepDirection	弧线绘制的方向。

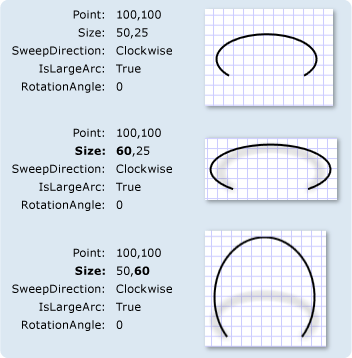
具体说明可以看这个文档。

用 Path 和 ArcSegment 可以很好地实现弧形的进度条，它的 XAML 如下：

<Path Stroke="SlateBlue"

      StrokeThickness="4">

    <Path.Data>

        <PathGeometry>

            <PathFigure IsClosed="False" StartPoint="30,170">

                <ArcSegment IsLargeArc="True"

                            Point="170,170"

                            Size="96,96"

                            SweepDirection="Clockwise" />

            </PathFigure>

        </PathGeometry>

    </Path.Data>

</Path>

叠加两个不同颜色的 Path，就可以实现这种效果：

Path 和 ArcSegment 是一个很正统的方案，前面提到的 RadialGauge 就用了这个方案。不过它的计算很麻烦，三角函数我已经忘光了。

另外，请注意弧线两端都是平平的直角，这和需求不符，而且微软的文档说过：

在 Windows 11 中，我们对窗口边框进行了圆角处理。我们的用户研究团队发现，圆润的几何图形在心理上提供一种安全感，并且使应用的 UI 更易于扫描。这使用户更少感觉威慑，也使应用更具吸引力。圆角处理的量也是精心选择的。我们公司对此进行了研究，努力在专业性、柔和感和吸引度之间取得平衡。

微软说得没错，这条弧线两端的直角确实让我感觉很没有有安全感。所以需要设置 StrokeStartLineCap 和 StrokeEndLineCap 这两个属性的值为 Round：

StrokeStartLineCap="Round" StrokeEndLineCap="Round"

它们控制线条两端边缘的轮廓，Round 表示一个直径等于线条粗细的半圆形。这样才能实现需求中的圆角：

顺便一提，这两个属性的类型是 PenLineCap 枚举，这个枚举的四个值分别代表以下几种形状：

3. 使用 Arc

第二个方案是使用 Microsoft.Expression.Drawing 中的 Arc 形状直接画出一个弧形。如果安装了旧版的 Blend（好像 2017 或以前的都可以），可以在 资产->形状 里找到这个形状（我装的是英文版所以没有中文截图）：

或者在 Nuget 上搜索 Microsoft.Expression.Drawing 找到一个符合自己项目的版本。

Arc 的用法很简单，只需要执行 StartAngle 和 EndAngle 即可输出一个弧形：

<ed:Arc ArcThickness="12"

        ArcThicknessUnit="Pixel"

        EndAngle="150"

        Fill="#101a26"

        StartAngle="-150"

        Stretch="None"

        StrokeEndLineCap="Round"

        StrokeStartLineCap="Round" />

叠加两个不同颜色的 Arc，可以实现这种效果：

可是仔细看，就算用了 StrokeStartLineCap 和 StrokeEndLineCap 两个属性，Arc 的两端任然是直角，这不仅不符合需求，而且微软的文档说过：

在 Windows 11 中，我们对窗口边框进行了圆角处理。我们的用户研究团队发现，圆润的几何图形在心理上提供一种安全感，并且使应用的 UI 更易于扫描。这使用户更少感觉威慑，也使应用更具吸引力。圆角处理的量也是精心选择的。我们公司对此进行了研究，努力在专业性、柔和感和吸引度之间取得平衡。

微软又说对了，这个方案弧线两端的直角确实让我感觉到威胁。所以这个方案简单但不完美，我还要尝试下一个方案。

4. 使用 Ellipse

这个方案还算有趣，Ellipse 明明是圆形，却能用来画弧形。为了用 Ellipse 显示进度，我们会用 StrokeDashArray 控制它的边框长度。StrokeDashArray 用于将边框变成虚线，它的值是一个 double 类型的有序集合，集合中的值指虚线中每一段的长度，长度单位是边框值的宽度。例如以下圆形：

<Ellipse StrokeDashArray="1,2,3"

         Stroke="#FFFF0EC4"

         StrokeThickness="10"

         Height="200"

         Width="200" />

边框宽度为 10，虚线的第一段是长度为 10 的实线，第二段为长度为 20 的空白，第三段为长度为 30 的实线，然后如此循环直到结束。

用 StrokeDashArray 做进度提示的基本做法就是将进度（Progress）通过 Converter 转换为分成两段的 StrokeDashArray，第一段为实线，表示当前进度，第二段为空白。假设一个 Shape 的边长是 100，当前进度为 50，则将 StrokeDashArray 设置成 {50，double.MaxValue} 两段。

为了实现弧形进度条，我们还需要控制 Ellipse 旋转的角度。具体来说我实现了一个 EllipseProgressBehavior，里面有 Progress、StartAngle 和 EndAngle 三个属性，具体代码在这里。用这个 Behavior 控制 Ellipse 的边框长度和旋转角度，使用方式如下：

<Ellipse Margin="4"

         Stroke="#7bcdd9"

         StrokeThickness="4">

    <interactivity:Interaction.Behaviors>

        <local1:EllipseProgressBehavior EndAngle="150"

                                        Progress="50"

                                        StartAngle="-150" />

    </interactivity:Interaction.Behaviors>

</Ellipse>

叠加两个 Ellipse，即可实现需求中的弧形进度条。可是这时候弧形的两端都是直角，即使设置了 StrokeStartLineCap 和 StrokeEndLineCap 两个属性都不起作用。微软的文档说过：

在 Windows 11 中，我们对窗口边框进行了圆角处理。我们的用户研究团队发现，圆润的几何图形在心理上提供一种安全感，并且使应用的 UI 更易于扫描。这使用户更少感觉威慑，也使应用更具吸引力。圆角处理的量也是精心选择的。我们公司对此进行了研究，努力在专业性、柔和感和吸引度之间取得平衡。

微软永远都是对的，这个方案弧线两端的直角确实让我感觉没有吸引力。

对于用 StrokeDashArray 显示的边框，不能使用 StrokeStartLineCap 和 StrokeEndLineCap 去控制它的两端的轮廓，而应该使用 StrokeDashCap：

StrokeDashCap="Round"

最终通过叠加两个 Ellipse 实现了户型进度条的需求：

5. 最后

童话和寓言都喜欢把相似的内容说上三次，例如三只小猪，三顾茅庐，弗利萨的三段变身。所以不是我在研究回字有多少种写法，我只是遵循古法想把一种技术讲透而已。

6. 参考

7. 源码

https://github.com/DinoChan/wpf_design_and_animation_lab