树行DP小结

顾名思义：就是在树上做的DP，依据DFS的性质，在访问过儿子之后返回后将儿子的状态传递给父亲...

先看例题：

此题用贪心也能过，不过正解是DP。

对于树上的DP我们可以直接考虑最优解下各点的状态来方便我们设状态.显然信号联通的树上各点只有三中状态，自己有塔，儿子有塔，父亲有塔.

那我们设状态时就可以用f[x][0],f[x][1],f[x][2]表示儿子有塔，自己有塔，父亲有塔...

对于1和2的状态比较好转移：

f[x][1]+=min(f[y][1],min(f[y][0],f[y][2]));

f[x][2]+=min(f[y][1],f[y][0]);

那对于0的状态，则可以枚举哪个儿子有塔，用计算好的f[x][2]的值：

f[x][0]=min(f[x][0],f[x][2]-min(f[y][1],f[y][0])+f[y][1]); （好好考虑）

初始化，f[x][1]=1;f[x][0]=INT_MAX;

代码：

#include<bits/stdc++.h>
#define _ 0
using namespace std;
const int maxn=10010;
int n,tot,link[maxn],f[maxn][4],fa[maxn]; //f[i][1]表示自己用。
struct bian                              //f[i][0]表示儿子用.f[i][2]表示父亲用.
{
    int y,next;
};
bian a[2*maxn];
inline void add(int x,int y)
{
    a[++tot].y=y;
    a[tot].next=link[x];
    link[x]=tot;
}
inline void dfs(int x)
{
    f[x][1]=1;f[x][0]=INT_MAX;
    for(int i=link[x];i;i=a[i].next)
    {
        int y=a[i].y;
        if(y==fa[x]) continue;
        fa[y]=x;
        dfs(y);
        f[x][1]+=min(f[y][1],min(f[y][0],f[y][2]));
        f[x][2]+=min(f[y][1],f[y][0]);
    }
    for(int i=link[x];i;i=a[i].next)
    {
        int y=a[i].y;
        if(y==fa[x]) continue;
        f[x][0]=min(f[x][0],f[x][2]-min(f[y][1],f[y][0])+f[y][1]);
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    cin>>n;
    for(int i=1;i<n;i++)
    {
        int x,y;
        cin>>x>>y;
        add(x,y);add(y,x);
    }
    dfs(1);
    cout<<min(f[1][1],f[1][0]);
    return (0^_^0);
}

下一题：

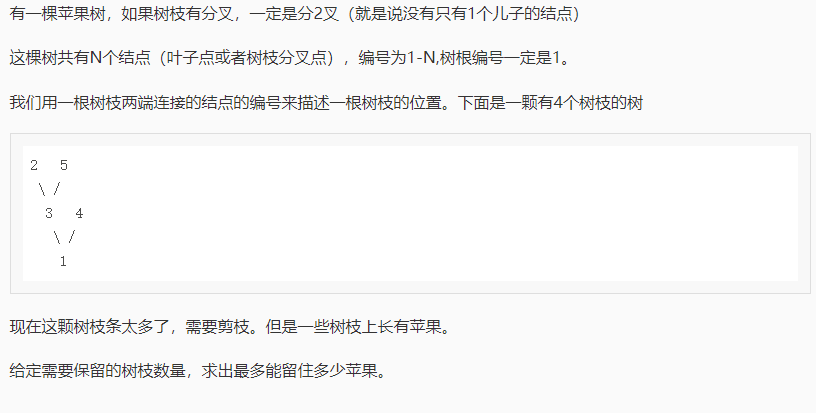
这道题同样是树上跑DP.

状态很好想，f[x][j]表示x的节点保留j条树枝的最大值.

#include<bits/stdc++.h>
#define _ 0
using namespace std;
const int maxn=110;
int n,Q,tot,link[maxn],f[maxn][maxn],size[maxn],fa[maxn],deep[maxn];
struct bian   //f[i][j]表示i点保留了j条边的最大苹果数.
{
    int y,v,next;
};
bian a[2*maxn];
inline void add(int x,int y,int v)
{
    a[++tot].y=y;
    a[tot].v=v;
    a[tot].next=link[x];
    link[x]=tot;
}
inline void dfs(int x)
{
    size[x]=1;
    for(int i=link[x];i;i=a[i].next)
    {
        int y=a[i].y;
        if(deep[y]) continue;
        deep[y]=deep[x]+1; //计算它的深度.
        dfs(y);
        size[x]+=size[y];  //计算以其为根节点的子树数量
        for(int j=min(Q-deep[x]+1,size[x]-1);j>=0;--j)   //见下
            for(int k=min(Q-deep[y]+1,min(size[y]-1,j-1));k>=0;--k) //见下
                f[x][j]=max(f[x][j],f[x][j-k-1]+f[y][k]+a[i].v);
    }
}
int main()
{
    freopen("1.in","r",stdin);
    cin>>n>>Q;
    for(int i=1;i<=n;i++)
    {
        int x,y,v;
        cin>>x>>y>>v;
        add(x,y,v);add(y,x,v);
    }
    deep[1]=1; //对深度初始化.
    dfs(1);
    cout<<f[1][Q]<<endl;
    return (0^_^0);
} 

这里主要讲j和k的范围，想说j，Q-deep[x]+1表示要想选到x这个点必须保留deep[x]+1个树枝.size[x]-1表示x此时最多选的树枝.

同理，k还多了个j-1，因为还要选x到y这条边，所以要建议.

这里警告我：状态转移必须在合理的范围内，否则会出现不可预计的后果.还有f循环的顺序考虑清楚.

例如此题j就必须是倒序的。因为是拿y来更新x的，比如假如正序:拿f[y][1]更新过f[x][2]后，又拿f[X][2]更新f[x][3]这就不符合情况.此时倒序，由大的枚举就不会出现这种情况了。

好了，就到这了.