感知机与支持向量机 (SVM)

感知机与SVM一样都是使用超平面对空间线性可分的向量进行分类，不同的是：感知机的目标是尽可能将所有样本分类正确，这种策略指导下得出的超平面可能有无数个，然而SVM不仅需要将样本分类正确，还需要最大化最小分类间隔，对SVM不熟悉的朋友可以移步我另一篇文章：支持向量机(SVM)之硬阈值 - ZhiboZhao - 博客园 (cnblogs.com)。

为了系统地分析二者的区别，本文还是首先介绍感知机模型，学习策略以及求解思路

一、感知机模型

还是假定在 \(p\) 维空间有 \(m\) 组训练样本对，构成训练集 $T = { (x_{1}, y_{1}), (x_{2}, y_{2}),...,(x_{n}, y_{n})} $，其中 \(x_{i} \in R^{1 \times p}\)，\(y_{i}\in \{-1, +1\}\)，以二维空间为例，在线性可分的情况下，所有样本在空间可以描述为：

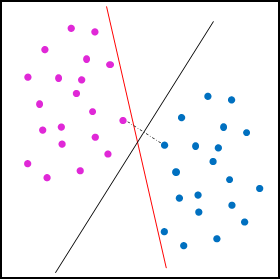
在上图中，紫色和蓝色的圆形代表不同的类别，红色的实线表示任意一条能够将这两种区分的超平面，理论上这种超平面有无数条，都有可能是感知机的解，然而SVM的模型解出来的超平面很有可能通过最大化最小间隔的策略得到的黑色的实线。我们将超平面表示为：\(\Phi: b+w_{1}x_{1}+w_{2}x_{2}+...+w_{p}x_{p} = 0\)，写成矩阵形式为：\(\Phi: w^{T}x + b = 0\)，根据高中数学的知识，可以得出 $ w $ 表示超平面的法向量，\(b\) 表示超平面的截距。感知机的最终目标可以表示为：

\[w^{T}x_{i}+b>0,\quad if \quad y_{i}=1\\
w^{T}x_{i}+b<0,\quad if \quad y_{i}=-1
\]

通过有监督的训练，不断地学习超平面的参数 \((w, b)\)，最终找到一个超平面 \(f(x) = w^{T}x + b\) 网络能够根据任意输入 \(x_{i}\) 输出对应的值来区分不同的模型。

二、感知机的学习策略

感知机是根据错误驱动的思想来进行学习，具体来说，先给待学习参数 \((w,b)\) 一个初始值，得到的初始超平面一般无法正确区分类别，我们用集合 \(D\) 来代表被错误分类的样本，那么最终的学习策略就是最小化被错误分类的点的个数，定量表示如下：

\[L(w,b) = \sum_{i=1}^{n}\psi (y_{i}(w^{T}x_{i}+b)
\]

函数 \(\psi(x)\) 定义为：

\[\psi(x) = 1, \quad if\quad x<0\\
\psi(x) = 0, \quad if\quad x>0
\]

因为当 \(y_{i}f(x_{i}) = y_{i}(w^{T}x_{i}+b) <0\) 时，该点被错误分类，于是损失函数 \(L(w,b)\) 就记录了总共被错误分类的个数，最小化loss就能求出超平面参数。

然而随着 \((w,b)\) 的改变，指示函数 \(\psi\) 要么为0，要么为1，是一个不连续的函数，因此损失函数不可导，也就不容易求出极值，需要将 \(L(w,b)\) 转换成 \((w,b)\) 的连续函数。

根据高中知识，我们得到空间内任意一点到超平面的距离为：

\[distance = \dfrac{1}{||w||}|w^{T}x_{i}+b|
\]

那么对于正确分类的正样本点，其到超平面的距离设为正数，对于正确分类的错样本点，其道超平面的距离设为复数，那么所有正确分类的样本到超平面的距离可以表示为：

\[d = y_{i}\dfrac{1}{||w||}(w^{T}x_{i}+b)
\]

因此，所有错误分类的样本的到超平面的总距离就可以表示为：

\[d = -y_{i}\dfrac{1}{||w||}(w^{T}x_{i}+b) \Longleftrightarrow -y_{i}(w^{T}x_{i}+b)
\]

所以，感知机的损失函数最终定义为：

\[L(w,b) = -\sum_{i\in D}y_{i}(w^{T}x_{i}+b)
\]

显然：

当正类样本被分成负类样本时 \(w^{T}x_{i}+b < 0,y_{i}>0\)，

当负类样本被分成正类样本时 \(w^{T}x_{i}+b > 0,y_{i}<0\)，

因此，损失函数是非负的，且分类错误的点就越少，分类错误的点就离超平面越近，其值越小。

三、感知机的求解算法

由于损失函数 \(L(w,b)\) 是自变量的连续函数，因此可以用随机梯度下降 (SGD) 的方式进行求解。那么损失函数的梯度如下：

\[\nabla_{w}L(w,b) = \dfrac{\partial L(w,b)}{\partial w} = -\sum_{x_{i} \in D}y_{i}x_{i}\\
\nabla_{b}L(w,b) = \dfrac{\partial L(w,b)}{\partial b} = -\sum_{x_{i} \in D}y_{i}
\]

采用随机梯度下降法更新的公式为：

\[w = w+\eta y_{i}x_{i};\quad b = b+\eta y_{i}
\]