oracle中net manager的配置

我们知道，要连接一个数据库需要知道四个参数：

1. 登陆用户名：user；

2. 登录密码：password；

3. 存放数据库的服务器地址（server_ip）和端口（server_port）；

4. 数据库名（db_name）；

我们如果要连接db_name这个数据，除了用户名密码以外，还需要输入类似“server_ip:server_port/db_name”这样一个连接字符串。

如上所述，对于一个数据库连接，我们常常需要记住server_ip、server_port 和 db_name 这三个要素。一旦管理的数据库多了，而且有许多数据库分布在不同的服务器、不同的端口上，记忆起来就容易产生混乱。为了解决这个问题，Oracle为我们提供了“命名服务”，可以通过打开Oracle Net Manager工具，选择“服务命名”进行配置。Oracle自己的解释是“服务命名文件夹用于配置本地命名方法。本地命名方法是命名方法之一，使用这种方法可以将简单名称、Net服务名解析为连接到数据库或服务所需的信息”。初次看到这段官方解释，往往很难看懂。我的理解是，所谓命名服务，其实就是一个将普通名字映射到某个连接字符串的 key-value 对，其中key就是这个“命名服务”的名称，可以自己任意选取，例如“abc”，以后在连接数据库的时候，只需要输入“abc”进行连接；服务器在收到“abc”之后，可以自动将其解析为它所对应的value，即连接到某个数据库的连接字符串，完成连接。

PS：此处的“命名服务”和“服务命名”本质上是一个东西，“命名服务”表示的是一种服务，而“服务命名”表示对这个服务的命名配置，说的是同一个事物的不同方面。

由上我们知道，要配置一个命名服务，就是要配置server_ip、server_port 和 db_name 这三个要素。下面介绍用图形界面配置命名服务的过程，在此之前假设已创建了一个数据库，全局数据库名为：kane.test。

1. 打开Oracle Net Manager工具，选择“服务命名”节点，点击左边绿色“+”按钮，弹出“Net 服务命名向导”

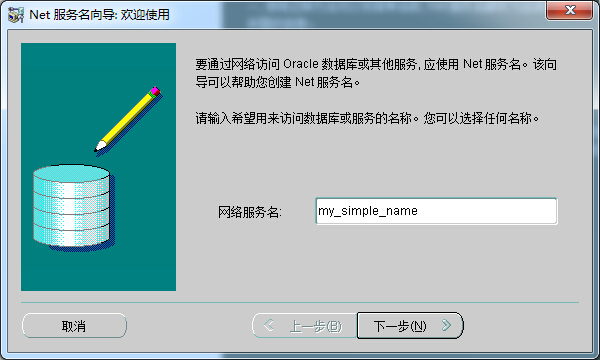
其中的“网络服务名”即自定义的服务名称，也即上面所说的key，可以任意选取，主要不和现有的服务命名冲突。假设这里取my_simple_name，单击“下一步”。

2. 选择通信协议：

这里默认使用 TCP/IP 协议。单击“下一步”。

3. 配置server_ip、server_port：

“主机名”即存放数据库的服务器地址，“端口号”采用默认的1521端口。单击“下一步”。

4. 配置db_name ：

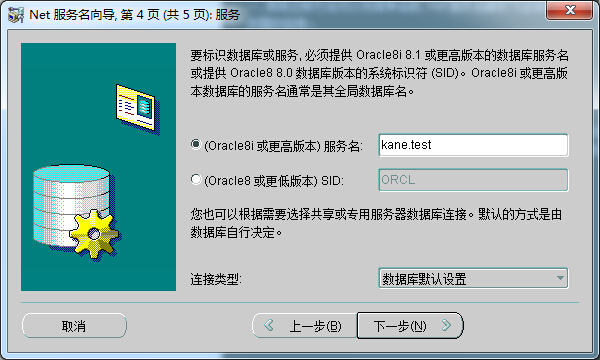
“（Oracle8i或更高版本）服务名”即填之前创建的数据库的全局数据库名。至此，一个服务命名的server_ip、server_port 和 db_name 三个要素都已配置完成。单击“下一步”。

5. 测试或完成：

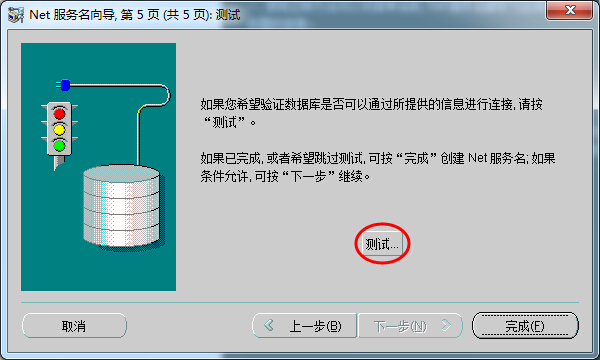
点击“完成”退出向导。或点击“测试”按钮测试以上配置是否正确：

请确认您测试所用的用户ID未被锁定。可以点击“更改登陆”按钮选择其他账户测试。如果还是测试失败，请返回检查以上每步的配置是否输入正确。

6. 此时回到Oracle Net Manager工具主界面，可以看到已经配置好的各项参数：

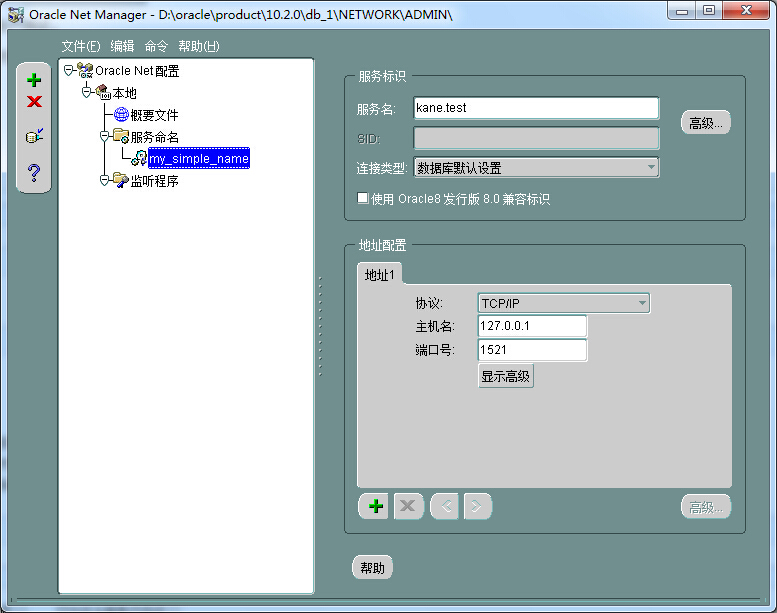
7. 此时一定不要忘了选择菜单“文件”——“保存网络配置”以使所做的更改生效。

8. PL/SQL登陆：

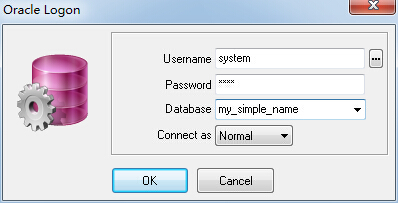
因为已经配置了名为“my_simple_name”的命名服务，所以此时在“Database”项只需要填写“my_simple_name”字符串即可连接成功。

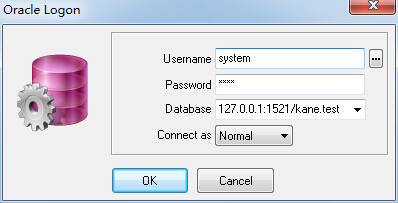
如果没有配置命名服务，则需要用户显示指定数据库服务器地址、端口和数据库名，以下参数也可成功连接：