Working out（DP）

题目描述：

题意：

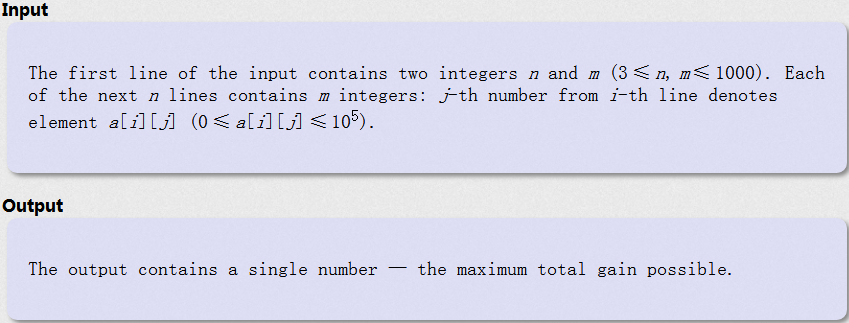
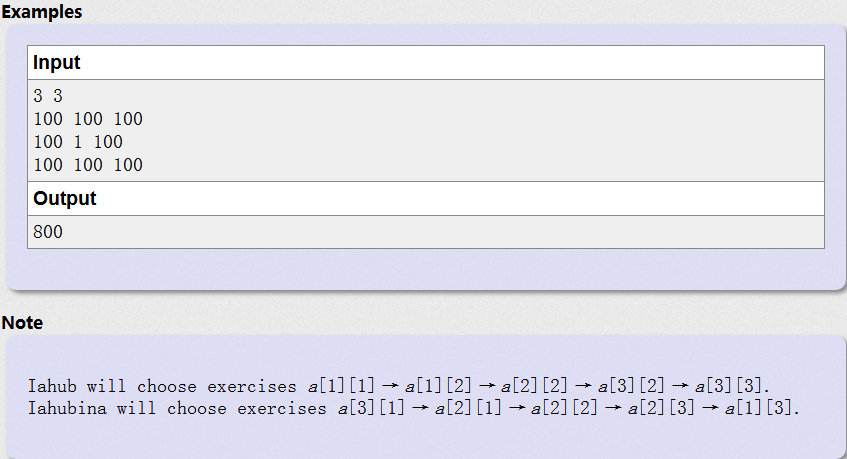
有n*m个格子, 走过一个格子可以得到相应的分数. 
A 从(1,1)沿 下 或 右 走到(n,m) 
B 从(n,1)沿 上 或 右 走到(1,m) 
两人路径有且只能有一个格子重合(重合格子的分数不算), 求两人分数之和的最大值.

首先要保证只有一个格子重合,那么只可能是以下两种情况: 
1) A向右走,相遇后继续向右走,而B向上走,相遇后继续向上走 
2) A向下走,相遇后继续向下走,而B向右走,相遇后继续向右走

接着枚举相遇的格子(i,j)即可,考虑四个方向的dp

dp1[i][j] := 从 (1, 1) 到 (i, j) 的最大分数 
dp2[i][j] := 从 (i, j) 到 (n, m) 的最大分数 
dp3[i][j] := 从 (n, 1) 到 (i, j) 的最大分数 
dp4[i][j] := 从 (i, j) 到 (1, m) 的最大分数

代码:

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int maxn=1e3+;
 int a[maxn][maxn];
 int dp1[maxn][maxn];//(1,1)-(i,j)
 int dp2[maxn][maxn];//(i,j)-(1,1)
 int dp3[maxn][maxn];//(n,1)-(i,j)
 int dp4[maxn][maxn];//(i,j)-(n,1)
 int main()
 {
     int n,m;
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++) scanf("%d",&a[i][j]);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++) dp1[i][j]=a[i][j]+max(dp1[i][j-],dp1[i-][j]);
     for(int i=n;i>=;i--)
         for(int j=m;j>=;j--)
         dp2[i][j]=a[i][j]+max(dp2[i][j+],dp2[i+][j]);
     for(int i=n;i>=;i--)
         for(int j=;j<=m;j++)
         dp3[i][j]=a[i][j]+max(dp3[i+][j],dp3[i][j-]);
     for(int i=;i<=n;i++)
         for(int j=m;j>=;j--)
         dp4[i][j]=a[i][j]+max(dp4[i][j+],dp4[i-][j]);
     int ans=;
     for(int i=;i<n;i++)
     for(int j=;j<m;j++)
     {
         ans=max(ans,dp1[i][j-]+dp2[i][j+]+dp3[i+][j]+dp4[i-][j]);
         ans=max(ans,dp3[i][j-]+dp4[i][j+]+dp2[i+][j]+dp1[i-][j]);
     }
     printf("%d\n",ans);
     return ;
 }

样例中的dp1,dp2,dp3,dp4最终结果为：

100  300
 201 400
300 400 500

500 400 300
400 201
300  100

300 400 500
 201 400
100  300

300  100
400 201
500 400 300

在最终求出结果时：

for(int i=2;i<n;i++)
{

　　for(int j=2;j<m;j++)
　　{
　　　　ans=max(ans,dp1[i][j-1]+dp2[i][j+1]+dp3[i+1][j]+dp4[i-1][j]);
　　　　ans=max(ans,dp3[i][j-1]+dp4[i][j+1]+dp2[i+1][j]+dp1[i-1][j]);
　　}

}

第一种情况下的ans的值为黄色部分值相加，第二种情况下的ans的值为蓝色部分值相加；