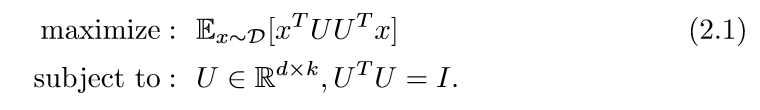Stochastic Optimization of PCA with Capped MSG
从这里回溯到此文章,这篇文章得作者是之前那篇文章的第三作者,里头提到的算法也及其相似,所以算是前者的基础吧。
Problem
这篇文章同样是关于PCA(在线或者说随机),试图寻找一个合适的\(k-\)维的子空间去压缩数据。
普通的PCA,是下面的这种形式:
但是因为这是一个非凸的问题,所以并不容易求解(特征分解然后去前k个主向量忽略,因为这时在线的或者说随机的)。
论文将这个问题进行了第一步放缩:
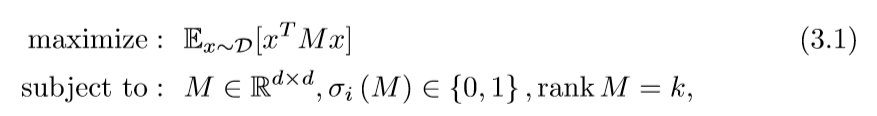
但是\(rankM=k\)这个条件依然不是凸的。
第二次放缩:
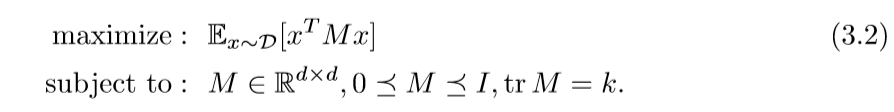
这一次问题和条件都是凸的了,所以这就是一个凸优化问题了。不过,作者刻意提及(3.1)的原因是,可以证明,(3.2)的最优解可以分解为(3.1)的解的凸线性组合[Warmuth, Kuzmin 2008]。
Matrix Stochastic Gradient
每一次迭代,都将进行下面的步骤:
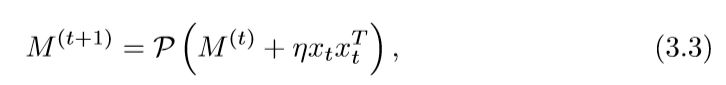
算法(MSG)
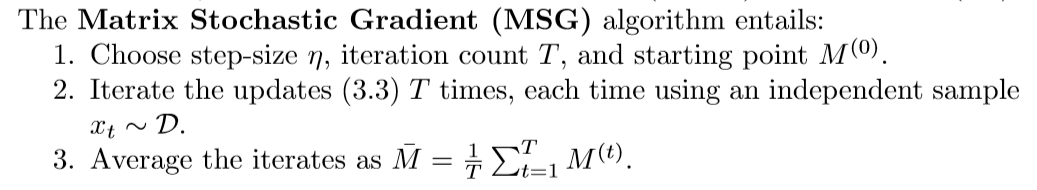
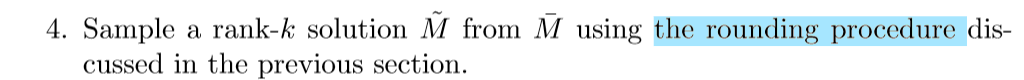
步骤二和步骤四会在下面讲到,问题是步骤三上,我不明白为什么需要取个平均值,我感觉直接取最后一个矩阵M就可以了。
步骤二(单次迭代)
算法

每一次迭代,都会先对\(M'+U'diag(\sigma')(U')^{\top}\)进行特征分解,但是并不是直接分解,而是使用了一个技巧,姑且称之为单步SVD,这个分解方法会利用之前\(M'\)的\(U'\)的结果。
单步SVD
为了方便,我们令\(\eta = 1\)且:

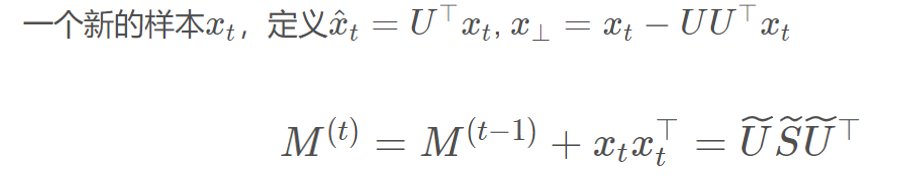
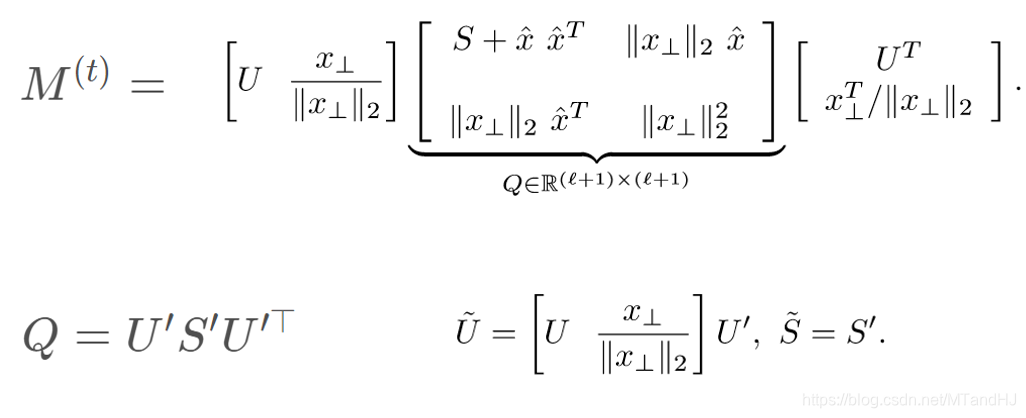
上面的算法就是先进行了单步SVD,然后再进行\(project()\)。为什么要进行这个\(project()\)呢,因为新的\(M\)并不满足(3.2)的\(tr(M)=k\)的条件,所以通过\(project()\),映射到一个新的矩阵。
这个矩阵是唯一的,且满足下面的性质:
- 迹为k,同时矩阵的特征向量和原来一样
- 最大特征值不会超过1
唯一性由下面这个引理给出

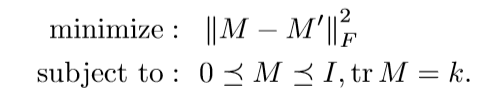
\(project()\)算法

这个算法看起来复杂,但目的很单纯。
\(\sigma_1 \quad \sigma_2 \: \mathop{\uparrow}\limits^{i}\: \sigma_3\ldots\sigma_m \:\mathop{\uparrow}\limits^{j} \: \sigma_{m+1} \quad \sigma_{m+2} \quad\)
注意上面的\(m+2\)个奇异值(从小到大排列),每个\(\sigma\)对应一个代表其个数\(\kappa\)。
\(i,j\)满足(i=0,1或者j=m+2为特殊情况):
\(\sigma_{i-1} + S<0\) \(\quad \sigma_{j+1} + S\geq 1\)
\(S\)根据上面算法的式子算的,且可验证,这样的S是一定存在的。
则,进行下面操作:
小于\(\sigma_i\)的奇异值截为0,大于等于\(\sigma_{j+1}\)的奇异值截为1,
其余的保持为\(\sigma+S\)
就这么经过\(T\)步的岁月,\(M\)来到了生命的尽头,站在悬崖上,朝远处眺望,夕阳、红霞分外美丽:
“啊!我的迹是\(k\),可我的秩呢?”说罢,老泪纵横。
没错,辛苦了这么久,我们得到(3.2)的解,接下来,就需要\(Rounding(M)\)使得迹为\(k\)的\(M\)的秩变为\(k\),这个问题,在之前的论文也提到了,当时不清楚,现在,其实也不怎么清楚,但好歹有个了解,不过我保证我讲不清楚,如果真的想知道,还是看论文吧——这是一种分解方法。
\(rounding()\)
来到:Here
Randomized Online PCA Algorithms with Regret Bounds that are Logarithmic in the Dimension
由Manfred K. Warmuth 和 Dima Kuzmi在08年发表的文章。
这篇论文挑个时间再好好看看吧,先把其中一部分在这里讲一下,但可能不对。



这里就只摆上三个算法吧。大概是这个意思,有个概率向量\(\mathsf{w}\),每个分量表示舍弃该主成分的概率,但我们都知道,舍弃了一部分,就会产生误差,\(\mathbb{l}\)就表示这个损失,每个分量表示舍弃该成分的一个损失(貌似单位化了)。
每次\(\mathsf{w}\)都会更新,根据损失。
论文稍微改进了一下,就是将\(\mathsf{w}\)分解为\(\mathop{\sum}\limits_{i}p_ir_i\),每个\(r_i\)都有\(n-k\)个非零项\(\frac{1}{n-k}\),这样,算法3就是先根据\(p_i\)采样到一个分解项\(r_j\),\(r_j\)中的非零项,表示对应成分是要被舍弃的,根据损失,对\(\mathsf{w}\)进行更新,循环往复。
当然这个算法如何应用到矩阵的选择上,根据后面的描述,应该是利用SVD,然后将其中的对角序列,看成\(\mathsf{w}\)进行选择,不过具体的还没怎么看,到时候再说吧。
Stochastic Optimization of PCA with Capped MSG的更多相关文章
- TensorFlow 深度学习笔记 Stochastic Optimization
Stochastic Optimization 转载请注明作者:梦里风林 Github工程地址:https://github.com/ahangchen/GDLnotes 欢迎star,有问题可以到I ...
- Stochastic Optimization Techniques
Stochastic Optimization Techniques Neural networks are often trained stochastically, i.e. using a me ...
- ADAM : A METHOD FOR STOCHASTIC OPTIMIZATION
目录 概 主要内容 算法 选择合适的参数 一些别的优化算法 AdaMax 理论 代码 Kingma D P, Ba J. Adam: A Method for Stochastic Optimizat ...
- (转) An overview of gradient descent optimization algorithms
An overview of gradient descent optimization algorithms Table of contents: Gradient descent variants ...
- First release of mlrMBO - the toolbox for (Bayesian) Black-Box Optimization
We are happy to finally announce the first release of mlrMBO on cran after a quite long development ...
- An overview of gradient descent optimization algorithms
原文地址:An overview of gradient descent optimization algorithms An overview of gradient descent optimiz ...
- 论文翻译:2021_Decoupling magnitude and phase optimization with a two-stage deep network
论文地址:两阶段深度网络的解耦幅度和相位优化 论文代码: 引用格式:Li A, Liu W, Luo X, et al. ICASSP 2021 deep noise suppression chal ...
- 【机器学习Machine Learning】资料大全
昨天总结了深度学习的资料,今天把机器学习的资料也总结一下(友情提示:有些网站需要"科学上网"^_^) 推荐几本好书: 1.Pattern Recognition and Machi ...
- FAQ: Machine Learning: What and How
What: 就是将统计学算法作为理论,计算机作为工具,解决问题.statistic Algorithm. How: 如何成为菜鸟一枚? http://www.quora.com/How-can-a-b ...
随机推荐
- java任意n以内连续的和等于n
import java.util.Scanner; /** * Created by Admin on 2017/3/25. */ public class test01 { public stati ...
- JMeter—常见问题(十四)
参考<全栈性能测试修炼宝典JMeter实战>第十五章 JMeter常见问题 1.无法产生负载 注意检查各元件是否时禁用状态.JMeter在运行时是以数形式加载各种元件的,如果父节点被禁用, ...
- java单元测试
单元测试 1.简介 在日常开发中,我们编写的任何代码都需要经过严谨的测试才可以发布.以往的测试方法都是通过编写一个main函数进行简单的测试,并使用大量的print语句输出结果,这种方法其实是不可取的 ...
- 阿里云ECS Ubuntu16.0 安装 uwsgi 失败解决方案
Ubuntu安装包时报错 E:Unable to locate package xxx(如:python3-pip) 一般新安装Ubuntu后需要先更新软件源: apt-get update apt- ...
- js在前端json字符串和对象互相转化
js在前端json字符串和对象互相转化 //对象转json串 注意:参数必须是对象,数组不起作用,对象格式{'0'=>'a'} JSON.stringify( arr ); //json字符串转 ...
- 创建 tomcat 服务的镜像
如何设计 Tomcat 的 Dockerfile $ sudo docker search tomcat |wc -l 285 在 dockerhub 上搜索与 tomcat 相关的镜像,有如此之多的 ...
- localhost和127.0.0.1及ip区别
1.127.0.0.1是回送地址,指本地机,一般用来测试使用.回送地址是本机回送地址(Loopback Address),即主机IP堆栈内部的IP地址,主要用于网络软件测试以及本地机进程间通信,无论什 ...
- java.util.concurrent包学习笔记(一)Executor框架
类图: 其实从类图我们能发现concurrent包(除去java.util.concurrent.atomic 和 java.util.concurrent.locks)中的内容并没有特别多,大概分为 ...
- 联想Y7000安装Ubuntu16.04/Win10双系统,wifi问题,显卡驱动和CUDA10安装
https://blog.csdn.net/la9881275/article/details/86720752 Ubuntu16.04系统安装拿到Ubuntu镜像制作装机优盘,这里就不写了.我的优盘 ...
- Redis之过期时间
1.命令介绍 expire key seconds 设置key的有效时间,单位为秒expire命令返回1表示设置成功,返回0表示键不存在或设置失败. ttl keyttl命令返回值是键的剩余时间 ...