目标检测中的mAP

一、IOU的概念

交集和并集的比例（所谓的交集和并集，都是预测框和实际框的集合关系）。如图：

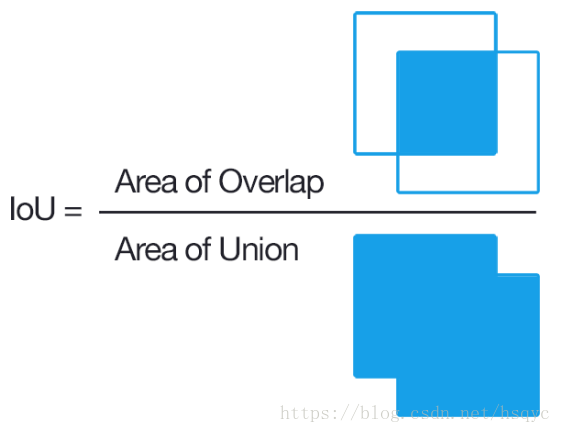
二、Precision（准确率）和Recall（召回率）的概念

对于二分类问题，可将样例根据其真实类别和预测类别组合划分为真正例（true positive）、假正例（false positive）、真反例（true negative）、假反例（false negative）

记为TP、FP、TN、FN，显然有TP + FP + TN + FN = 样例总数。这里着重提一下真正例的含义：预测是正例，实际上也是正例。主要它是准确率P和召回率R的分子

混淆矩阵如下：

准确率P和召回率R分别定义为：

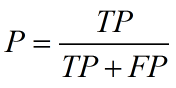
预测的正例：TP + FP

真实的正例：TP + FN

P的含义：真正的正例占预测正例的比例。衡量的是一个分类器预测出的正例是真实正例的概率

R的含义：真正的正例占真实正例的比例。衡量的是一个分类器找出所有正例的能力。

准确率和召回率是一对矛盾的度量。一般来说，准确率高，则召回率低；准确率低，则召回率高。光靠精度还不能衡量分类器的好坏程度。比如50个正样本和50个负样本，我的分类器把49个正样本和50个负样本都分为负样本，剩下一个正样本分为正样本。这样我的准确率也是100%，但是这样的分类器根本就不能用。

两个极端：如果召回率100%，就是所有的正例都被找出来了。（非常简单，就是将所有的例子都判为正例。你看，你不是要我找到所有的正例吗？我不管好坏，全部判为正例，这样所有的正例不都找到了吗？），但是这样的分类器没用，因为它一个反例都没有排除。

如果召回率为0%，就是一个正例都没有找到。同样，将所有的例子判为反例，这样的分类器同样没用。

三、PR曲线

我们将分类器判别的正例分为TP、FP，我们凭什么这么干？IoU阈值就是评价标准。如果IoU的值超过一定的阈值，即分类器认为找到一个正例。而这个阈值是可以设置的。

由此可知，召回率和准确率受到了阈值设置的影响，而且阈值对于两个指标的影响是相反的：阈值增加则准确率增加，召回率降低，反之亦然。那么我们可以通过设置一系列的阈值来得到一系列的（准确率，召回率）的指标对，然后利用这些指标对画出坐标图，这就是PR曲线。

四、举例计算mAP

有3张图如下，要求算法找出face。蓝色框代表实际框（label），绿色框代表算法给出的预测框（prediction），旁边红色的小字代表的是置信度，设定第一张图的预测框为pre1，第一张的标签框叫label1。第二张、第三张同理。

1. 根据IoU计算TP、FP

首先，我们计算每张图的pre和label的IoU，根据IoU是否大于0.5来判断该pre是属于TP、还是FP。显然，pre1是TP、pre2是FP，pre3是TP

2. 排序

根据每个pre的置信度进行从高到低排序，这里pre1、pre2、pre3从高到低

3. 在不同置信度阈值下获得Precision和Recall

首先设置阈值为0.9，无视所有小于0.9的pre。那么检测器检出所有框pre即TP+FP（预测的正例） = 1，并且pre1是TP，那么Precision=1/1，所以Recall=1/3。这样就得到一组P、R值。

然后设置阈值为0.8，无视所有小于0.8的pre。那么检测器检出所有框pre即TP+FP（预测的正例） = 2，并且pre1是TP，那么Precision=1/2。而真实的正例有三个，所以Recall=1/3。这样就又得到一组P、R值。

然后设置阈值为0.7，无视所有小于0.7的pre。那么检测器检出所有框pre即TP+FP（预测的正例） = 3，并且pre1、pre3是TP，那么Precision=2/3。而真实的正例有三个，所以Recall=2/3。这样就又得到一组P、R值。

4. 绘制PR曲线并计算AP值

根据上面3组PR值绘制PR曲线如下，然后每个"峰值点"往左画一条线段直到与上一个峰值点的垂直线相交。这样画出来的红色线段与坐标轴围起来的面积就是AP值

AP = 1*1/3 + (1/3)*(2/3) = 5/9 ≈ 0.56

5. 计算mAP

而mAP就是所有AP的平均值。比如有两个类，A类的AP为0.5，B类的AP为0.3，则mAP = （0.5 + 0.3) / 2 = 0.4

参考地址：

https://blog.csdn.net/hsqyc/article/details/81702437