CodeForces 283C World Eater Brothers

World Eater Brothers

题解：

树DP， 枚举每2个点作为国家。 然后计算出最小的答案。

首先我们枚举根， 枚举根了之后， 我们算出每个点的子树内部和谐之后的值是多少。

这样val[root]就是这个root为根的花费。

然后我们再fdfs一遍这棵树。

假如我们枚举u这个点是另一个国家，

则花费就是

1. root --- u 的路径上 保证路径上的点可以从 u 走到 或者就是 root 出发走到。

这个东西可以通过O1求得。

我们假设一个数组 记录下 root ---- u 之间的边。

1 表示为是正向边， -1表示为 反向边。

则我们需要这个数列修改完边的结果为 +++++ ------ 不能出现+-+ 或者 -+-。

现在假设这个数列的长度为len。

我们需要找到一个i 使得  1 <= i 的数都是 1，  >i && <= n的数都是 -1。

那对于这个i的花费就是  (i-sum[i])/2 + ( (len-i)-(sum[len] - sum[i])) => (len + sum[len])/2 - sum[i]。  sum为这个数列的前缀和。

可以发现枚举完某个点之后， len + sum[len]都是定值， 需要找到最大的sum[i]就好了， 并且这个sum[i]前面不会改变， 所以我们这个sum[i]也可以做个前缀和， 找到最大的那个值。

2. val[u]

也就是使得u子树和谐的花费。

3. tmp_val

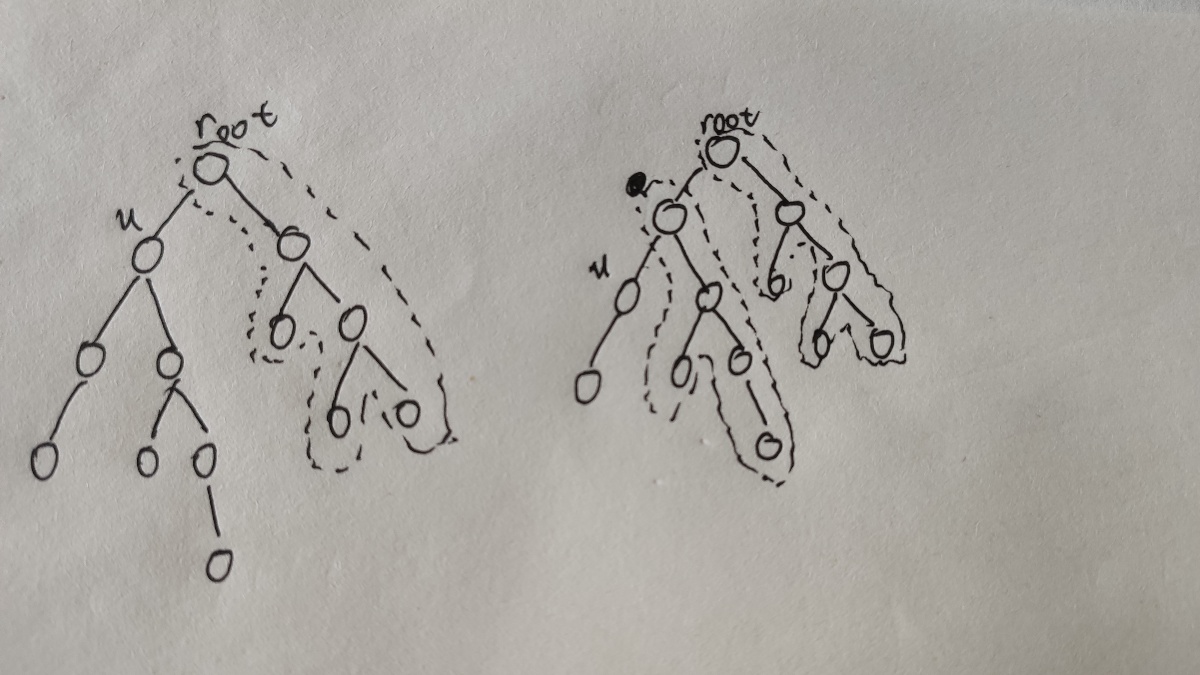
使得除了 root --- u路径上的点都和谐的花费。

也就是上图中的 虚线框起来的边的花费。

这3块总和就是答案了。

然后在所有枚举的过程中找最小值。

代码：

#include<bits/stdc++.h>
using namespace std;
#define Fopen freopen("_in.txt","r",stdin); freopen("_out.txt","w",stdout);
#define LL long long
#define ULL unsigned LL
#define fi first
#define se second
#define pb push_back
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define lch(x) tr[x].son[0]
#define rch(x) tr[x].son[1]
#define max3(a,b,c) max(a,max(b,c))
#define min3(a,b,c) min(a,min(b,c))
typedef pair<int,int> pll;
const int inf = 0x3f3f3f3f;
const int _inf = 0xc0c0c0c0;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const LL _INF = 0xc0c0c0c0c0c0c0c0;
const LL mod =  (int)1e9+;
const int N = 4e3;
vector<pll> vc[N];
int val[N];
int ans = inf;
int tmp_val = ;
void dfs(int o, int u){
    val[u] = ;
    for(pll t : vc[u]){
        int v = t.fi;
        if(v == o) continue;
        dfs(u, v);
        val[u] += val[v] + (t.se == -);
    }
}
void fdfs(int deep, int sum, int Max, int o, int u){
    if(o){
        ans = min(ans, (deep+sum)/ - Max+tmp_val+val[u]);
    }
    for(pll t : vc[u]){
        int v = t.fi;
        if(v == o) continue;
        tmp_val += val[u] - (val[v] + (t.se == -));
        fdfs(deep+, sum+t.se, max(Max, sum+t.se),u, v);
        tmp_val -= val[u] - (val[v] + (t.se == -));
    }

}
int main(){
    int n;
    scanf("%d", &n);
    for(int i = , u, v; i < n; ++i){
        scanf("%d%d", &u, &v);
        vc[u].pb(make_pair(v, ));
        vc[v].pb(make_pair(u,-));
    }
    for(int i = ; i <= n; ++i){
        dfs(, i);
        ans = min(ans, val[i]);
        tmp_val = ;
        fdfs(, , ,, i);
    }
    cout << ans << endl;
    return ;
}