codeforces 689E E. Mike and Geometry Problem(组合数学)

题目链接：

E. Mike and Geometry Problem

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike wants to prepare for IMO but he doesn't know geometry, so his teacher gave him an interesting geometry problem. Let's definef([l, r]) = r - l + 1 to be the number of integer points in the segment [l, r] with l ≤ r (say that 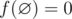). You are given two integers nand k and n closed intervals [li, ri] on OX axis and you have to find:

In other words, you should find the sum of the number of integer points in the intersection of any k of the segments.

As the answer may be very large, output it modulo 1000000007 (109 + 7).

Mike can't solve this problem so he needs your help. You will help him, won't you?

 

Input

 

The first line contains two integers n and k (1 ≤ k ≤ n ≤ 200 000) — the number of segments and the number of segments in intersection groups respectively.

Then n lines follow, the i-th line contains two integers li, ri ( - 109 ≤ li ≤ ri ≤ 109), describing i-th segment bounds.

 

Output

 

Print one integer number — the answer to Mike's problem modulo 1000000007 (109 + 7) in the only line.

 

Examples

 

input

3 2
1 2
1 3
2 3

output

5

input

3 3
1 3
1 3
1 3

output

3

input

3 1
1 2
2 3
3 4

output

6

题意：

在n个区间里选k个,得到的f等于区间交的点数;求所有的选择方案的和;

思路：

对于每个点可以发现,当这个点被num个线段覆盖时,这个点就会被选C(num,k)次,ans=∑C(num,k);
但是区间很大,点的数目居多,所以不可能一个点一个点的这样算,可以发现,相邻的点如果被相同数目的线段覆盖,那么这些点就可以合并成一个区间，所以ans=∑len*C(num,k),len表示这个区间点的个数;看这个点被覆盖了多少次可以采用跟树状数组那样的方法,左右端点+-1;

AC代码：

//#include <bits/stdc++.h>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define For(i,j,n) for(int i=j;i<=n;i++)
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef  long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<''||CH>'';F= CH=='-',CH=getchar());
    for(num=;CH>=''&&CH<='';num=num*+CH-'',CH=getchar());
    F && (num=-num);
}
int stk[], tp;
template<class T> inline void print(T p) {
    if(!p) { puts(""); return; }
    while(p) stk[++ tp] = p%, p/=;
    while(tp) putchar(stk[tp--] + '');
    putchar('\n');
}

const LL mod=1e9+;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=2e5+;
const int maxn=;
const double eps=1e-;

int n,k,l[N],r[N];
LL dp[N];

map<int,int>mp;

LL pow_mod(int x,LL y)
{
    LL s=,base=(LL)x;
    while(y)
    {
        if(y&)s=s*base%mod;
        base=base*base%mod;
        y>>=;
    }
    return s;
}

void Init()
{
    dp[k]=;
    For(i,k+,N)
    {
        LL x=i,temp=pow_mod(x-k,mod-);
        dp[i]=dp[i-]*x%mod*temp%mod;
    }
}
vector<int>ve;
int main()
{
    read(n);read(k);
    Init();
    For(i,,n)
    {
        read(l[i]);
        mp[l[i]-]++;
        ve.push_back(l[i]-);
        read(r[i]);
        mp[r[i]]--;
        ve.push_back(r[i]);
    }
    sort(ve.begin(),ve.end());
    LL ans=;
    int num=,prepo=-1e9-;
    int w=ve.size();
   for(int i=;i<w;i++)
    {
        int tempo=ve[i],len=tempo-prepo;
        if(num>=k)ans=ans+dp[num]*(LL)len%mod,ans%=mod;
       if(prepo!=tempo) prepo=tempo,num+=mp[tempo];
    }
    cout<<ans<<"\n";
        return ;
}