蚁群算法（Java）tsp问题

 

1、理论概述

1.1、TSP问题

旅行商问题，即TSP问题（旅行推销员问题、货郎担问题），是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个组合优化问题。该问题可以被证明具有NP计算复杂性，迄今为止，这类问题中没有一个找到有效解决算法，因此我们经常用一些近似求解算法，遗传算法、蚁群算法、粒子群算法等等。

1.2、蚁群算法

蚁群算法是一种仿生学算法，是由自然界中蚂蚁觅食的行为而启发的。在自然界中，蚂蚁觅食过程中，蚁群总能够按照寻找到一条从蚁巢和食物源的最优路径。以下是蚁群觅食过程：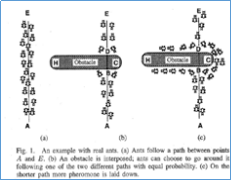

在图1（a）中，一群蚂蚁从A到E觅食，由于是直线路径，所以蚂蚁直接从源到目的地。在A和E之间多了一个障碍物（b）图，那么在H点或者C点的蚂蚁将要做选择，由于一开始路上没有前面蚂蚁留下的信息素，蚂蚁朝着两个方向行进的概率是相等的。但是当有蚂蚁走过时，它将会在它行进的路上释放出信息素，并且这种信息素会以一定的速率散发掉。它后面的蚂蚁通过路上信息素的浓度，做出决策，往左还是往右。很明显，沿着短边的的路径上信息素将会越来越浓，随着时间的增长，右边路径的信息素浓度会因为路径的长度而散发掉，所以会有越来越多的蚂蚁沿着较短的路径前行。如图c。

蚁群算法的缺点是收敛速度慢，容易陷入局部最优解。

2、算法流程

假设蚁群中所有蚂蚁的数量为m，所有城市之间的信息素用矩阵pheromone表示，最短路径为bestLength，最佳路径为bestTour。每只蚂蚁都有自己的内存，内存中用一个禁忌表（Tabu）来存储该蚂蚁已经访问过的城市，表示其在以后的搜索中将不能访问这些城市；还有用另外一个允许访问的城市表（Allowed）来存储它还可以访问的城市；另外还用一个矩阵（Delta）来存储它在一个循环（或者迭代）中给所经过的路径释放的信息素；还有另外一些数据，例如一些控制参数(α，β，ρ，Q)用于辅助计算信息素挥发、下一个城市选中概率等等，该蚂蚁行走完全程的总成本或距离（tourLength）等。假定算法总共运行maxgen次，运行时间为t。图三是算法流程图。（注：实验系数的选定是多次试验计算的结果见论文table1）

2.1、每只蚂蚁行进过程

为每只蚂蚁选择下一个节点，该节点只能从未选择节点中以某种概率搜索到，首先计算城市选中概率，之后以一定的原则计算下一步要选的城市，如果该城市没去过，则下一个城市就是该城市。本实验的选择方式是，产生一个随机数，顺序计算各个城市的选中概率之和，直到大于该随机数，则选择循环系数代表的城市（前提是该城市没选过。）遍历完所有节点后，将起始节点加入到 tour中，形成一个完整回路。保留回路长度 tourlength。接下来计算每个蚂蚁的信息素矩阵值。最后计算最佳路径，比较每个蚂蚁的路径成本，然后和bestLength比较，若它的路径成本比bestLength小，则将该值赋予bestLength，并在本次迭代中输出最优路径。本次迭代每只蚂蚁走完后结束。只要没有到达指定的迭代次数，则蚂蚁重新随机重置起始点，进入下一次迭代。

2.2、实验终止

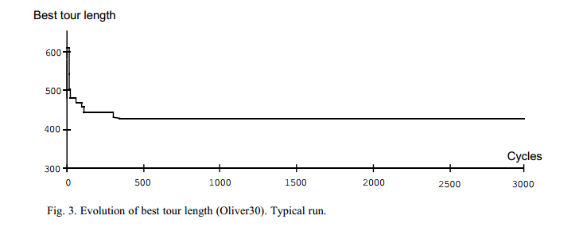
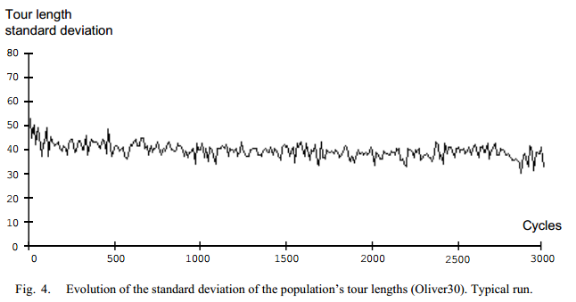
如果达到最大迭代次数maxgen，算法终止，输出最优路径和最优路径长度；否则，重新初始化所有的蚂蚁的信息，并且重新选择起始位置为每只蚂蚁。根据几次的实验结果表明，在迭代次数较大的时候（>1000）基本在250次迭代以内就能达到收敛路径长，即达到局部最优。由于每次试验的结果不同，也表明蚁群算法容易陷入局部最优，而非每次都可以得到全局最优，当然，迭代次数少，可能最优的路径长还未得到就已经迭代结束。由于没有与其他算法作比较，对于蚁群算法收敛速度慢这个缺陷无法比较。

（2）

路径误差：

图三

2.3、数据来源

本次试验数据来源于TSPLib,http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/。为方便实验，数据只要包含城市总数，城市编号，城市横纵坐标即可。

图四为算法数据流程图：

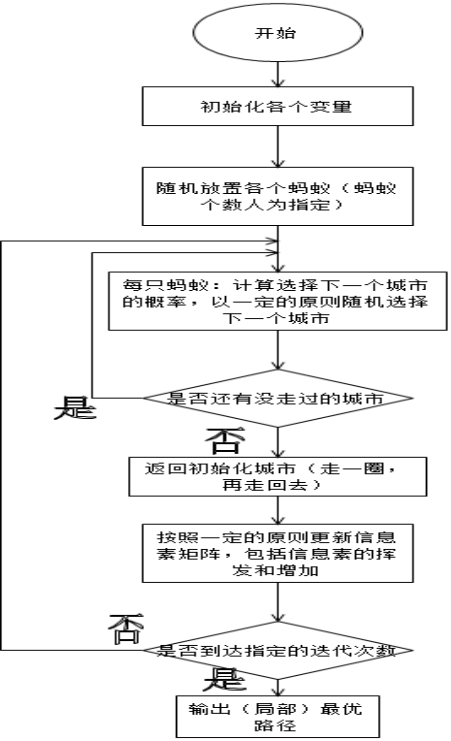
图四

论文中的算法描述：

 

3、算法实现描述

工程主要包括：蚂蚁类、蚁群算法、主调程序。

3.1、蚂蚁类主要包括以下几点：

顺序参观城市记录 int[]tour，城市是否参观记录int[] unvisitedcity，蚂蚁所走的总路长int tourlength，城市数目；方法主要有随机城市选择函数 void RandomSelectCity(int citycount)，下一个城市选择函数 void SelectNextCity(int index,double[][]tao,int[][]distance)和总路程长度计算函数 void CalTourLength(int [][]distance)。

3.2、蚁群算法主要包括以下几点：

数据成员：

ant []ants; //定义蚂蚁群

int antcount;//蚂蚁的数量

int [][]distance;//表示城市间距离

double [][]tao;//信息素矩阵

int citycount;//城市数量

int[]besttour;//求解的最佳路径

int bestlength;//求的最优解的长度

方法成员：

初始化函数，初始化文件信息，信息素矩阵，上述变量，蚂蚁初始位置等信息void init(String filename,int antnum)。

蚁群算法主要运行程序，包括迭代次数为实验参数，记录每一只蚂蚁的行进过程，计算本次迭代的这群蚂蚁的最优路径长，如果出现更短的路径，更新路径记录变量，迭代一次之后更新信息素矩阵以及蚂蚁重新初始化最初位置，知道到达指定迭代次数，输出收敛路径长。经过几次试验表明，一般在100次内可以达到一个收敛值，后续的若干次的剩余的迭代次数输出的路径长基本不变了。但是必须要到指定的迭代次数才会停止实验。

3.3、主程序包括以下几点：

调用蚁群算法，给定蚂蚁数量，城市信息文件，迭代次数，最后输出最优（局部）路径结果。蚁群算法内部，在对蚂蚁行进记录时会调用蚂蚁类的城市选择函数。

3.4、类关系图：

 

 import java.io.*;
 /**
  *蚁群优化算法，用来求解TSP问题
  */
 public class ACO {

     ant []ants; //定义蚂蚁群
     int antcount;//蚂蚁的数量
     int [][]distance;//表示城市间距离
     double [][]tao;//信息素矩阵
     int citycount;//城市数量
     int[]besttour;//求解的最佳路径
     int bestlength;//求的最优解的长度
     //filename tsp数据文件
     //antnum 系统用到蚂蚁的数量
     public void init(String filename,int antnum) throws FileNotFoundException, IOException{
         antcount=antnum;
         ants=new ant[antcount];
         //读取数据tsp里的数据包括第I个城市与城市的X,Y坐标
         int[] x;
         int[] y;
         String strbuff;
         BufferedReader tspdata = new BufferedReader(new InputStreamReader(new FileInputStream(filename)));
         strbuff = tspdata.readLine();//读取第一行，城市总数（按文件格式读取）
         citycount = Integer.valueOf(strbuff);
         distance = new int[citycount][citycount];
         x = new int[citycount];
         y = new int[citycount];
         for (int citys = 0; citys < citycount; citys++) {
             strbuff = tspdata.readLine();
             String[] strcol = strbuff.split(" ");
             x[citys] = Integer.valueOf(strcol[1]);//读取每排数据的第2二个数字即横坐标
             y[citys] = Integer.valueOf(strcol[2]);
         }
         //计算两个城市之间的距离矩阵，并更新距离矩阵
         for (int city1 = 0; city1 < citycount - 1; city1++) {
             distance[city1][city1] = 0;
             for (int city2 = city1 + 1; city2 < citycount; city2++) {
                 distance[city1][city2] = (int) (Math.sqrt((x[city1] - x[city2]) * (x[city1] - x[city2])
                         + (y[city1] - y[city2]) * (y[city1] - y[city2])));
                 distance[city2][city1] = distance[city1][city2];//距离矩阵是对称矩阵
             }
         }
         distance[citycount - 1][citycount - 1] = 0;
         //初始化信息素矩阵
         tao=new double[citycount][citycount];
         for(int i=0;i<citycount;i++)
         {
             for(int j=0;j<citycount;j++){
                 tao[i][j]=0.1;
             }
         }
         bestlength=Integer.MAX_VALUE;
         besttour=new int[citycount+1];
         //随机放置蚂蚁
         for(int i=0;i<antcount;i++){
             ants[i]=new ant();
             ants[i].RandomSelectCity(citycount);
         }
     }
     //maxgen ACO的最多循环次数
     public void run(int maxgen){
         for(int runtimes=0;runtimes<maxgen;runtimes++){
             //每次迭代，所有蚂蚁都要跟新一遍，走一遍
             //System.out.print("no>>>"+runtimes);
             //每一只蚂蚁移动的过程
             for(int i=0;i<antcount;i++){
                 for(int j=1;j<citycount;j++){
                     ants[i].SelectNextCity(j,tao,distance);//每只蚂蚁的城市规划
                 }
                 //计算蚂蚁获得的路径长度
                 ants[i].CalTourLength(distance);
                 if(ants[i].tourlength<bestlength){
                     //保留最优路径
                     bestlength=ants[i].tourlength;
                     //runtimes仅代表最大循环次数，但是只有当，有新的最优路径的时候才会显示下列语句。
                     //如果后续没有更优解（收敛），则最后直接输出。
                     System.out.println("第"+runtimes+"代(次迭代)，发现新的最优路径长度："+bestlength);
                     for(int j=0;j<citycount+1;j++)
                         besttour[j]=ants[i].tour[j];//更新路径
                 }
             }
             //更新信息素矩阵
             UpdateTao();
             //重新随机设置蚂蚁
             for(int i=0;i<antcount;i++){
                 ants[i].RandomSelectCity(citycount);
             }
         }
        }
     /**
      * 更新信息素矩阵
      */
     private void UpdateTao(){
         double rou=0.5;
         //信息素挥发
         for(int i=0;i<citycount;i++)
             for(int j=0;j<citycount;j++)
                 tao[i][j]=tao[i][j]*(1-rou);
         //信息素更新
         for(int i=0;i<antcount;i++){
             for(int j=0;j<citycount;j++){
                 tao[ants[i].tour[j]][ants[i].tour[j+1]]+=1.0/ants[i].tourlength;
             }
         }
     }
     /* 输出程序运行结果
      */
     public void ReportResult(){
         System.out.println("最优路径长度是"+bestlength);
         System.out.println("蚁群算法最优路径输出：");
         for(int j=0;j<citycount+1;j++)
             System.out.print( besttour[j]+">>");//输出最优路径
     }
 }

 import java.util.Random;
 /*
  蚂蚁类
  */
 public class ant {
     /**
      * 蚂蚁获得的路径
      */
     public int[]tour;//参观城市顺序
     //unvisitedcity 取值是0或1，1表示没有访问过，0表示访问过
     int[] unvisitedcity;
     /**
      * 蚂蚁获得的路径长度
      */
     public int tourlength;//某蚂蚁所走路程总长度。
     int citys;//城市个数
 /**
  * 随机分配蚂蚁到某个城市中
  * 同时完成蚂蚁包含字段的初始化工作
  * @param citycount 总的城市数量
  */
     public void RandomSelectCity(int citycount){
         citys=citycount;
         unvisitedcity=new int[citycount];
         tour=new int[citycount+1];
         tourlength=0;
         for(int i=0;i<citycount;i++){
             tour[i]=-1;
             unvisitedcity[i]=1;
         }//初始化各个变量

         long r1 = System.currentTimeMillis();//获取当前时间
         Random rnd=new Random(r1);
         int firstcity=rnd.nextInt(citycount);//随机指定第一个城市
         unvisitedcity[firstcity]=0;//0表示访问过
         tour[0]=firstcity;//起始城市
     }
     /**
      * 选择下一个城市
      * @param index 需要选择第index个城市了
      * @param tao   全局的信息素信息
      * @param distance  全局的距离矩阵信息
      */
     public void SelectNextCity(int index,double[][]tao,int[][]distance){
         double []p;
         p=new double[citys];//下一步要走的城市的选中概率
         //计算选中概率所需系数。
         double alpha=1.0;
         double beta=2.0;
         double sum=0;
         int currentcity=tour[index-1];//蚂蚁所处当前城市
         //计算公式中的分母部分（为下一步计算选中概率使用）
         for(int i=0;i<citys;i++){
             if(unvisitedcity[i]==1)//没走过
                 sum+=(Math.pow(tao[currentcity][i], alpha)*
                         Math.pow(1.0/distance[currentcity][i], beta));
         }
         //计算每个城市被选中的概率
         for(int i=0;i<citys;i++){
             if(unvisitedcity[i]==0)
                 p[i]=0.0;//城市走过了，选中概率就是0
             else{
                 //没走过，下一步要走这个城市的概率是？
                 p[i]=(Math.pow(tao[currentcity][i], alpha)*
                         Math.pow(1.0/distance[currentcity][i], beta))/sum;
             }
         }
         long r1 = System.currentTimeMillis();
         Random rnd=new Random(r1);
         double selectp=rnd.nextDouble();
         //轮盘赌选择一个城市；
         double sumselect=0;
         int selectcity=-1;
         //城市选择随机，直到n个概率加起来大于随机数，则选择该城市
         for(int i=0;i<citys;i++){//每次都是顺序走。。。。。
             sumselect+=p[i];
             if(sumselect>=selectp){
                 selectcity=i;
                 break;
             }
         }
         if (selectcity==-1)//这个城市没有走过
             System.out.println();
         tour[index]=selectcity;
         unvisitedcity[selectcity]=0;
     }
     /**
      * 计算蚂蚁获得的路径的长度
      * @param distance  全局的距离矩阵信息
      */
     public void CalTourLength(int [][]distance){
         tourlength=0;
         tour[citys]=tour[0];//第一个城市等于最后一个要到达的城市
         for(int i=0;i<citys;i++){
             tourlength+=distance[tour[i]][tour[i+1]];//从A经过每个城市仅一次，最后回到A的总长度。
         }
     }
 }

 import java.io.FileNotFoundException;
 import java.io.IOException;
 import java.util.logging.Level;
 import java.util.logging.Logger;
 //蚁群算法求解旅行商问题，TSP数据来源
 //http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/
 //数据中包括城市总量，每个城市的横纵坐标
 public class Main {
     /**
      * @param args the command line arguments
      */
     public static void main(String[] args) {
         ACO aco;
         aco=new ACO();
         try {
             aco.init("att48.txt", 100);//城市信息文件，蚂蚁数量
             aco.run(1000);//迭代次数
             aco.ReportResult();
         } catch (FileNotFoundException ex) {
             Logger.getLogger(Main.class.getName()).log(Level.SEVERE, null, ex);
         } catch (IOException ex) {
             Logger.getLogger(Main.class.getName()).log(Level.SEVERE, null, ex);
         }
     }
 }