HihoCoder 1121 二分图一•二分图判定

二分图一•二分图判定

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

大家好，我是小Hi和小Ho的小伙伴Nettle，从这个星期开始由我来完成我们的Weekly。

新年回家，又到了一年一度大龄剩男剩女的相亲时间。Nettle去姑姑家玩的时候看到了一张姑姑写的相亲情况表，上面都是姑姑介绍相亲的剩男剩女们。每行有2个名字，表示这两个人有一场相亲。由于姑姑年龄比较大了记性不是太好，加上相亲的人很多，所以姑姑一时也想不起来其中有些人的性别。因此她拜托我检查一下相亲表里面有没有错误的记录，即是否把两个同性安排了相亲。

OK，让我们愉快的暴力搜索吧！

才怪咧。

对于拿到的相亲情况表，我们不妨将其转化成一个图。将每一个人作为一个点(编号1..N)，若两个人之间有一场相亲，则在对应的点之间连接一条无向边。(如下图)

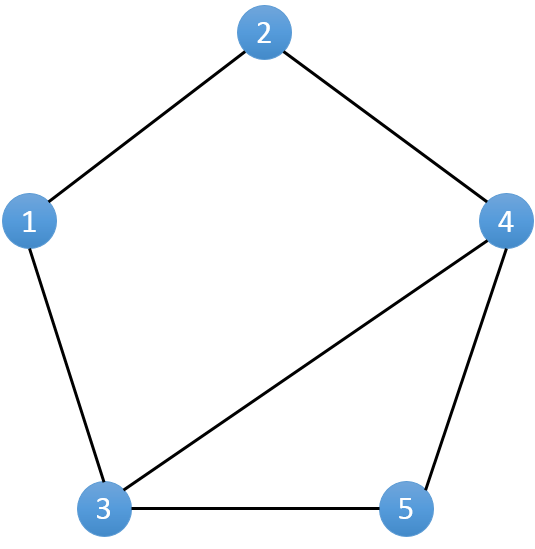
因为相亲总是在男女之间进行的，所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色，女性的节点染色黑色。对于得到的无向图来说，即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色，则表示这一条边所表示的记录有误。

由于我们并不知道每个人的性别，我们的问题就转化为判定是否存在一个合理的染色方案，使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。

那么，我们不妨将所有的点初始为未染色的状态。随机选择一个点，将其染成白色。再以它为起点，将所有相邻的点染成黑色。再以这些黑色的点为起点，将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)

在染色的过程中，我们应该怎样发现错误的记录呢？相信你一定发现了吧。对于一个已经染色的点，如果存在一个与它相邻的已染色点和它的颜色相同，那么就一定存在一条错误的记录。(如上图的4，5节点)

到此我们就得到了整个图的算法：

1. 选取一个未染色的点u进行染色
2. 遍历u的相邻节点v：若v未染色，则染色成与u不同的颜色，并对v重复第2步；若v已经染色，如果 u和v颜色相同，判定不可行退出遍历。
3. 若所有节点均已染色，则判定可行。

接下来就动手写写吧！

输入

第1行：1个正整数T(1≤T≤10)

接下来T组数据，每组数据按照以下格式给出：

第1行：2个正整数N,M(1≤N≤10,000，1≤M≤40,000)

第2..M+1行：每行两个整数u,v表示u和v之间有一条边

输出

第1..T行：第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”，否则输出”Wrong”

样例输入

2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5

样例输出

Wrong
Correct

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<memory>
using namespace std;
const int maxn=;
int col[maxn],n,m;
int Laxt[maxn],Next[maxn],To[maxn],cnt;
void add(int u,int v)
{
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;
    To[cnt]=v;
}
void init()
{
    cnt=;
    memset(Laxt,,sizeof(Laxt));
    memset(col,,sizeof(col));
}
int read()
{
    char c=getchar();int s=;
    while(c>''||c<'') c=getchar();
    while(c>=''&&c<=''){s=s*+c-'';c=getchar();}
    return s;
}
bool dfs(int v,int c)
{
    for(int i=Laxt[v];i;i=Next[i]){
        if(col[To[i]]==c) return false;
        if(!col[To[i]]){
            col[To[i]]=-c;
            if(!dfs(To[i],-c)) return false;
        }
    }
    return true;
}
bool check()
{
    for(int i=;i<=n;i++){
        if(col[i]) continue;
        col[i]=;
        if(!dfs(i,)) return false;
    }
    return true;
}
int main()
{
    int i,j,T,u,v;
    scanf("%d",&T);
    while(T--){
        init();
        scanf("%d%d",&n,&m);
        for(i=;i<=m;i++){
            u=read();v=read();
            add(u,v);add(v,u);
        }
        if(check()) printf("Correct\n");
        else printf("Wrong\n");
    }
    return ;
}