BZOJ4869：[SHOI2017]相逢是问候——题解

http://www.lydsy.com/JudgeOnline/problem.php?id=4869

题面复制于洛谷：https://www.luogu.org/problemnew/show/P3747#sub

参考洛谷的前两篇（也是仅有的两篇）题解。

首先我们要知道一个公式：

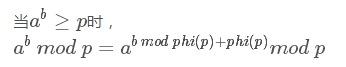
这又被叫做扩展欧拉定理，证明我们并不关心。

有了扩展欧拉定理，我们就能够避免高精度从而求出对于任意一个数的0操作之后变成什么数了。

（递归或者迭代选一个，递归好理解，迭代有助于理解下面的题解，而且常数小）

我们又有一个结论，对于一个p，它无限递归p=phi(p)直到p=1为止的深度为O(logp)。

这样的好处在于我们虽然修改了很多次，但是当修改次数大于logp的时候，此时你再怎么修改也没有用了因为你的指数为1相当于没有操作。

那么显然对于1我们记录该元素被操作了几次，然后暴力修改即可，可用线段树维护。复杂度O(nlognlogp)。（请注意这个复杂度是假的）

这样的复杂度我们交到bzoj上是没有问题的，但是交到洛谷上会TLE3个点。将递归改成迭代，预处理每个p的phi，各种常数优化也会TLE2个点。

emmm……why？

当然是因为我们的复杂度没算对啊。

对于单点修改，显然每次修改是O(logplogp)……等等，怎么多出来一个O(logp)。

忘了我们使用了快速幂了吗，我们多出来的O(logp)就是这么来的。

考虑除掉这个O(logp)，显然预处理快速幂。

如果你写的是迭代的话，你就会发现底数永远都是c不变，变的只是指数和模数， 且指数最大是p=1e8。

我们可以先求出不同模数且指数<=1e5的c的幂，我们还可以求不同模数且指数=整1e5的c的幂。

这就很像分块了，显然当我们要求指数为k时，k=x*1e5+y（y<1e5）显然可求。

这样我们预处理出所有的数在多少次操作后的值，则我们的复杂度就是O(nlognlogp)。

吐槽：最开始学完扩欧之后觉得这题洛谷给的难度高了，怎么就NOI+了，后来在TLE之后一看woc还有这种操作……

神题神题……

（然而博主并不想写正解，放的代码只能过bzoj，正解如果有时间的话会补上的emmm）

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cctype>
#include<map>
using namespace std;
typedef long long ll;
const int N=5e4+;
const int O=1e4+;
inline int read(){
    int X=,w=;char ch=;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch))X=(X<<)+(X<<)+(ch^),ch=getchar();
    return w?-X:X;
}
struct tree{
    ll v,t;
}tr[N*];
int su[O],he[O],cnt,phi[],n,m;
ll p,c,logp,b[N];
bool ok;
inline ll qpow(ll k,int p){
    ll ans=,s=c;
    while(k){
        if(k&)ans=ans*s;
        s*=s;k>>=;
        if(s>=p)ok=,s%=p;
        if(ans>=p)ok=,ans%=p;
    }
    return ans;
}
int Euler(int k){
    int res=k;
    for(int i=;su[i]*su[i]<=k;i++){
        if(k%su[i]==){
            res-=res/su[i];
            while(k%su[i]==)k/=su[i];
        }
    }
    if(k>)res-=res/k;
    return res;
}
void prime(){
    for(int i=;i<O;i++){
        if(he[i]==){
            cnt++;
            su[cnt]=i;
        }
        for(int j=;j<=cnt&&i*su[j]<O;j++){
            he[su[j]*i]=;
            if(i%su[j]==)break;
        }
    }
    phi[logp]=p;
    while(phi[logp]!=)phi[++logp]=Euler(phi[logp-]);
    phi[++logp]=;
}
void build(int a,int l,int r){
    if(l==r){
        tr[a].v=b[l]%p;
        return;
    }
    int mid=(l+r)>>;
    build(a<<,l,mid);build(a<<|,mid+,r);
    tr[a].v=(tr[a<<].v+tr[a<<|].v)%p;
}
ll suan(ll v,ll k){
    ll tmp=v;
    if(tmp>phi[k])tmp=tmp%phi[k]+phi[k];
    for(int i=k;i>;i--){
        ok=;tmp=qpow(tmp,phi[i-]);
        if(ok)tmp+=phi[i-];
    }
    return tmp;
}
void gai(int a,int l,int r,int l1,int r1){
    if(tr[a].t>=logp)return;
    if(r<l1||r1<l)return;
    if(l==r){
        tr[a].t++;
        tr[a].v=suan(b[l],tr[a].t);
        return;
    }
    int mid=(l+r)>>;
    gai(a<<,l,mid,l1,r1);gai(a<<|,mid+,r,l1,r1);
    tr[a].v=(tr[a<<].v+tr[a<<|].v)%p;
    tr[a].t=min(tr[a<<].t,tr[a<<|].t);
}
ll wen(int a,int l,int r,int l1,int r1){
    if(r<l1||r1<l)return ;
    if(l1<=l&&r<=r1)return tr[a].v;
    int mid=(l+r)>>;
    return (wen(a<<,l,mid,l1,r1)+wen(a<<|,mid+,r,l1,r1))%p;
}
int main(){
    n=read(),m=read(),p=read(),c=read();
    prime();
    for(int i=;i<=n;i++)b[i]=read();
    build(,,n);
    for(int i=;i<=m;i++){
        int op=read(),l=read(),r=read();
        if(!op)gai(,,n,l,r);
        else printf("%lld\n",wen(,,n,l,r));
    }
    return ;
}

+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。 　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++