【动态规划】POJ1661 Help Jimmy

Help Jimmy

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 11621		Accepted: 3827

Description

"Help Jimmy" 是在下图所示的场景上完成的游戏。 

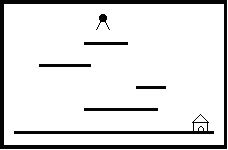
场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。

Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。

设计一个程序，计算Jimmy到底地面时可能的最早时间。

Input

第一行是测试数据的组数t（0 <= t <= 20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i = 1..N）。所有坐标的单位都是米。

Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。

Output

对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。

Sample Input

1
3 8 17 20
0 10 8
0 10 13
4 14 3

Sample Output

23

Source

POJ Monthly--2004.05.15 CEOI 2000

 

试题分析：设状态dp[i][0]为第i块木板左边落下的最小时间

                      dp[i][1]为第i块木板右边落下的最小时间

               那么容易得出转移方程

dp[i][0]=min(dp[i][0],dp[j][0]+abs(a[j].X1-a[i].X1)+a[i].H-a[j].H);
                   dp[i][0]=min(dp[i][0],dp[j][1]+abs(a[j].X2-a[i].X1)+a[i].H-a[j].H);

dp[i][1]=min(dp[i][1],dp[j][0]+abs(a[j].X1-a[i].X2)+a[i].H-a[j].H);
                   dp[i][1]=min(dp[i][1],dp[j][1]+abs(a[j].X2-a[i].X2)+a[i].H-a[j].H);

 当然，前提是j块木板的高度差不能超过MAX且第i块木板落下到第j块木板(这个可以预处理)

               这个题要倒着做！倒着做！

               开始正着做了一遍，把discuss中的数据测光了也是对的，莫名其妙WA了一小时 TAT

               后来花了10分钟重写了一个正着做的就一遍AC了……

此题需要注意的细节：

①MEMSET inf

②落到板子的边缘也算落在板子上

③在高度允许情况下可以直接落到地上

④abs

是否感觉有些反人类思维呢？听说最短路可以过TAT

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<stack>
#include<vector>
#include<algorithm>
//#include<cmath>

using namespace std;
const int INF = 9999999;
#define LL long long

inline int read(){
	int x=0,f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*f;
}
int N,X,Y,MAX;
int T;
struct data{
	int X1,X2,H;
}a[1001];
int dp[1001][2];
int down[1001][2];
int fir;
bool flag=false;

bool cmp(data a,data b){
    return a.H>b.H;
}

void pre(){//预处理
	sort(a+1,a+N+1,cmp);//sort一定要加
	bool flag1=false,flag2=false;
	for(int i=1;i<=N;i++){//记录第i块板子左/右落下会落到哪里
		flag1=false,flag2=false;
		for(int j=i+1;j<=N;j++){
			if(flag1&&flag2) break;
			if(a[i].H>a[j].H){
				if(a[j].X1<=a[i].X1&&a[j].X2>=a[i].X1&&!flag1) down[i][0]=j,flag1=true;
				if(a[j].X2>=a[i].X2&&a[j].X1<=a[i].X2&&!flag2) down[i][1]=j,flag2=true;
			}
		}
		if(!flag1) down[i][0]=N+1;//N+1板子为地面
		if(!flag2) down[i][1]=N+1;
	}
	a[N+1].H=0;a[N+1].X1=-INF,a[N+1].X2=INF;
	for(int i=1;i<=N+1;i++){//预处理从初始点落下会落到哪里
		if(Y-a[i].H<=MAX)
		    if(a[i].X1<=X&&a[i].X2>=X){
		        fir=i;
		        break;
		    }
	}
    if(fir==N+1){
		printf("%d\n",Y);//可以直接落到地面上，直接输出
		flag=true;
	}
	return ;
}

int main(){
	T=read();
	while(T--){
		flag=false;
	    N=read(),X=read(),Y=read(),MAX=read();
        for(int i=1;i<=N;i++){
        	a[i].X1=read();
        	a[i].X2=read();
        	a[i].H=read();
		}
		memset(dp,INF,sizeof(dp));//memset
		pre();
		if(flag) continue;
		dp[N+1][0]=0;
		dp[N+1][1]=0;
		dp[N][1]=dp[N][0]=a[N].H;
		for(int i=N-1;i>=fir;i--){
			for(int j=i+1;j<=N+1;j++){
				if(abs(a[i].H-a[j].H)>MAX) break;//如果高度差已经大于MAX直接退出
				if(down[i][0]==j){//dp
					if(j!=N+1){
				        dp[i][0]=min(dp[i][0],dp[j][0]+abs(a[j].X1-a[i].X1)+a[i].H-a[j].H);
				        dp[i][0]=min(dp[i][0],dp[j][1]+abs(a[j].X2-a[i].X1)+a[i].H-a[j].H);
				    }
				    else dp[i][0]=min(dp[i][0],a[i].H);
				}
				if(down[i][1]==j){
					if(j!=N+1){
				        dp[i][1]=min(dp[i][1],dp[j][0]+abs(a[j].X1-a[i].X2)+a[i].H-a[j].H);
				        dp[i][1]=min(dp[i][1],dp[j][1]+abs(a[j].X2-a[i].X2)+a[i].H-a[j].H);
				    }
				    else dp[i][1]=min(dp[i][1],a[i].H);
			    }
			}
		}
		printf("%d\n",min(dp[fir][0]+abs(a[fir].X1-X)+abs(Y-a[fir].H),dp[fir][1]+abs(a[fir].X2-X)+abs(Y-a[fir].H)));
	}
	return 0;
}