scikit-FEM-例1-求解Possion边值问题

"""
Author: kinnala

Solve the problem -∇²u = 1 with zero boundary conditions on a unit square.
"""

from skfem import *

调入 skfem 宏包

m = MeshTri()
m.refine(4)

三角剖分网格(MeshTri)，加密（refine） $4$ 次

e = ElementTriP1()
basis = InteriorBasis(m, e)

ElememtTriP1: 三角形线性有限元 $ P_1 $

InteriorBasis: 节点基函数

@bilinear_form
def laplace(u, du, v, dv, w):
    return du[0]*dv[0] + du[1]*dv[1]

调用双线性形式模块 @bilinear_form

定义 laplace 函数

@linear_form
def load(v, dv, w):
    return 1.0*v

调用线性泛函模块@linear_form

定义 load 函数

A = asm(laplace, basis)
b = asm(load, basis)

组装刚度矩阵  $A$

组装质量向量  $b$

I = m.interior_nodes()

取出内部网格  I

x = 0*b
x[I] = solve(*condense(A, b, I=I))

求解方程  $Ax=b$

if __name__ == "__main__":
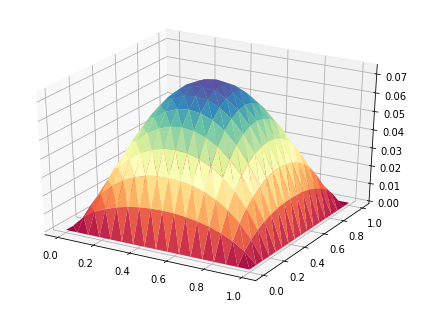
    m.plot3(x)
    m.show()

画出解的图象：