POJ3056：The Bavarian Beer Party(区间DP)

Description

The professors of the Bayerische Mathematiker Verein have their annual party in the local Biergarten. They are sitting at a round table each with his own pint of beer. As a ceremony each professor raises his pint and toasts one of the other guests in such a way that no arms cross.



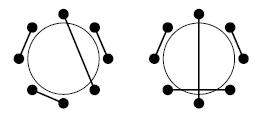
Figure 2: Toasting across a table with eight persons:no arms crossing(left), arms crossing(right)

We know that the professors like to toast with someone that is drinking the same brand of beer, and we like to maximize the number of pairs of professors toasting with the same brand , again without crossing arms. Write an algorithm to do this, keeping in mind that every professor should take part in the toasting.

Input

The frist line of the input contains a single number: the number of test cases to follow. Each test case has the following format:

One line with an even number p, satisfying 2 <= p <= 1000: the number of participants

One line with p integers (separated by single spaces) indicating the beer brands fro the consecutive professors( in clockwise order, starting at an arbitrary position). Each value is between 1 and 100 (boudaries included).

Output

For every test case in the input, the output should contain a single number on a single line: the maximum number of non-intersecting toasts of the same beer brand for this test case.

Sample Input

2
6
1 2 2 1 3 3
22
1 7 1 2 4 2 4 9 1 1 9 4 5 9 4 5 6 9 2 1 2 9

Sample Output

3
6

题意：有偶数个人，所有人都必须互相敬酒，而且不能交叉，问在这种情况下，互相敬酒的人牌子相同的最大对数

思路：又是一道比较简单的区间DP，要注意的是，所有人都必须敬酒，而且不能交叉，这种情况分区间解决即可

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

int t,n,a[1005],dp[1005][1005],i,j,k,l;

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(i = 1; i<=n; i++)
            scanf("%d",&a[i]);
        memset(dp,0,sizeof(dp));
        for(l = 1; l<n; l+=2)//l代表是一个区间内头与尾的间距，因为不能交叉，所以两头尾之间相隔的的人数必须为0,2,4..等偶数
        {
            for(i = 1; i+l<=n; i++)
            {
                j = i+l;
                dp[i][j] = dp[i+1][j-1];
                if(a[i] == a[j])//头尾相等，对数加1
                    dp[i][j]++;
                for(k = i+1; k<j; k+=2)//分割的区间也是同样道理
                    dp[i][j] = max(dp[i][j],dp[i][k]+dp[k+1][j]);
            }
        }
        printf("%d\n",dp[1][n]);
    }

    return 0;
}