●BOZJ 3144 [Hnoi2013]切糕

题链：

http://www.lydsy.com/JudgeOnline/problem.php?id=3144

题解：

"这是一个经典的最小割模型" ---引用自别人的博客
。。。。。。。。。。。。。
苦酒入喉心作痛，我怎么就是建不出图呢？

先考虑部分限制：
1).每个纵轴上只选择一个点。
    这个建图比较简单，如下，（把点权放在它上方的边上）：

(x,y,z) –> (x,y,z+1) : (w[x][y][z])
   
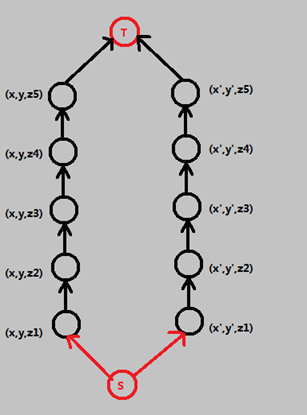
    只用求一个最小割即可。
另外，再添加另一个限制：
2).相邻的纵轴上选择的点的竖直距离不超过D（假设 D=1）

(x,y,z) –> (x',y',z-D ) : (INF)   (x,y)与（x'，y'相邻）
    这个就只有 kou nao dai 了。。。
    因为在上图中每条路上只割一条边。
    那么假设在左边的路上割了 E1。
    那么显然，只能在右边的路上割黄色区域。
    如果建一条绿边（竖直向下D个单位）的话，显然右边黄色区域下面的边就割不了了。
   
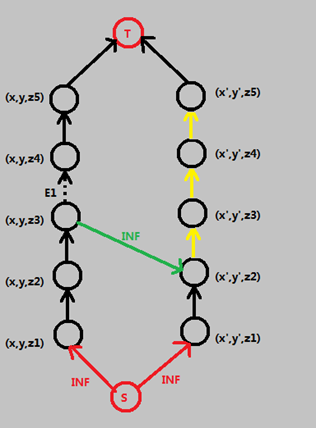
    那么又是如何限制黄色区域的上界的呢。
    考虑如果选择割了右边黄色区域上面的某一条边 E2,
    那类似绿边那样的建一条蓝色的边，
    显然这无法形成一个割，因为存在可继续增广的路。
     
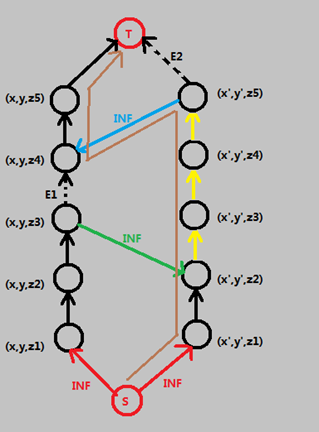
    所以为了形成最下割，在右边的选择区域就固定在了黄色区域里。

代码：

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 100050
#define MAXM 1000050
#define INF 0x3f3f3f3f
using namespace std;
const int mv[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
struct Edge{
	int to[MAXM],cap[MAXM],nxt[MAXM],head[MAXN],ent;
	void Init(){ent=2;}
	void Adde(int u,int v,int w){
		to[ent]=v; cap[ent]=w; nxt[ent]=head[u]; head[u]=ent++;
		to[ent]=u; cap[ent]=0; nxt[ent]=head[v]; head[v]=ent++;
	}
	int Next(int i,bool type){
		return type?head[i]:nxt[i];
	}
}E;
int d[MAXN],cur[MAXN];
int P,Q,R,D,S,T;
int idx(int x,int y,int z){
	return P*Q*(z-1)+(x-1)*Q+y;
}
bool bfs(){
	queue<int>q; int u,v;
	memset(d,0,sizeof(d));
	q.push(S); d[S]=1;
	while(!q.empty()){
		u=q.front(); q.pop();
		for(int i=E.Next(u,1);i;i=E.Next(i,0)){
			v=E.to[i];
			if(d[v]||!E.cap[i]) continue;
			d[v]=d[u]+1; q.push(v);
		}
	}
	return d[T];
}
int dfs(int u,int reflow){
	if(u==T||!reflow) return reflow;
	int flowout=0,f,v;
	for(int &i=cur[u];i;i=E.Next(i,0)){
		v=E.to[i];
		if(d[v]!=d[u]+1) continue;
		f=dfs(v,min(reflow,E.cap[i]));
		flowout+=f; E.cap[i^1]+=f;
		reflow-=f;	E.cap[i]-=f;
		if(!reflow) break;
	}
	if(!flowout) d[u]=0;
	return flowout;
}
int Dinic(){
	int flow=0;
	while(bfs()){
		memcpy(cur,E.head,sizeof(E.head));
		flow+=dfs(S,INF);
	}
	return flow;
}
int main()
{
	E.Init();
	scanf("%d%d%d%d",&P,&Q,&R,&D);
	S=P*Q*R+1; T=P*Q*R+2;
	for(int k=1,x,_i,_j,to;k<=R;k++)
		for(int i=1;i<=P;i++)
			for(int j=1;j<=Q;j++){
				scanf("%d",&x);
				if(k==R) to=T; else to=idx(i,j,k+1);
				E.Adde(idx(i,j,k),to,x);
				if(k-D<=0) continue;
				for(int l=0;l<4;l++){
					_i=i+mv[l][0];
					_j=j+mv[l][1];
					if(_i<1||P<_i||_j<1||Q<_j) continue;
					E.Adde(idx(i,j,k),idx(_i,_j,k-D),INF);
				}
			}
	for(int i=1;i<=P;i++)
		for(int j=1;j<=Q;j++)
			E.Adde(S,idx(i,j,1),INF);
	int ans=Dinic();
	printf("%d",ans);
	return 0;
}