二：状压dp

一：状压dp的基本特征

状态压缩问题一般是指用十进制的数来表示二进制下的状态

这种用一个数来表示一组数，以降低表示状态所需的维数的解题手段，就叫做状态压缩。

常用到位运算

二：位运算

&：与运算，相同为1不同为0

| ：或运算，全0位0，否则为1

^：异或运算，不同为1，相同为0（也叫半加与运算）

<<：左移操作，x<<j，x在二进制下向左移j位,（也就是原来的数乘j即：x*=j）右边用0填充，反码不同，要用1填充（负数）

>>：右移操作，x>>j相当于x=/j，左边反码，补码补1（负数）

例：

1.判断一个数字x在二进制下的第i位是不是为1if(((1<<(i-1))&x)>0)

将1左移i-1位，相当于制造了一个只有第i位为1其他位都是0的二进制数，然后用该数与x做与运算

2.把一个数字x在二进制下的第x为更改为1

x|=(1<<(i-1))

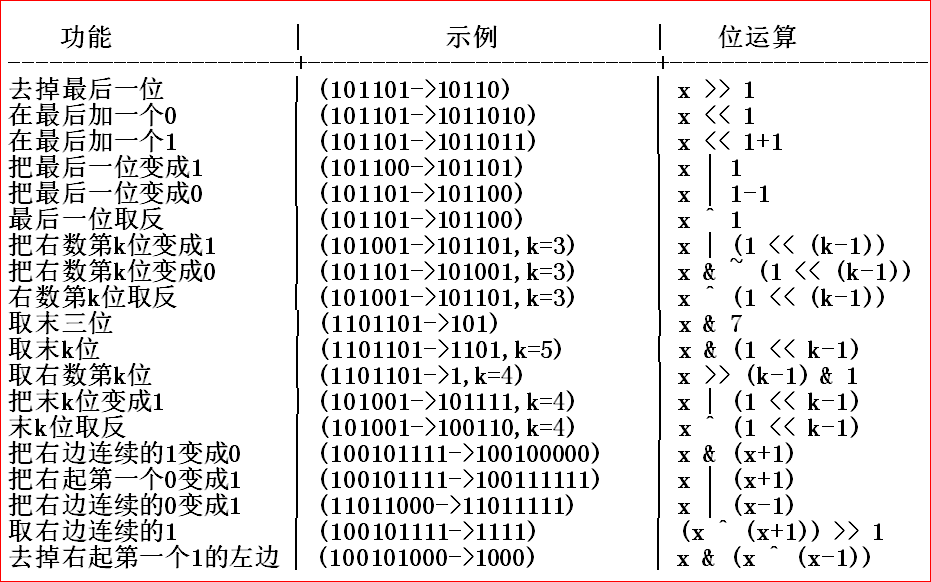
eg：

有一个n*m的棋盘（1<=n<=5,1<=m<=1000）现有1*2和2*1的小木块无数

要想盖满整个棋盘有多少种方法，答案大于1000000007，mod1000000007。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
int N, M;    //n,m分别代表棋盘的长宽
][];    //dp[i][j]表示对于前i-1行，第i行采用第j（一个十进制的数）种状态时，得到的方案可行的总数　　
void dfs(int i,int j,int state,int nex)    //这里i代表列数，j代表当前位数(也可以说是行数-1，初始时为0)，state代表状态数，nex代表下一列出现的状态
{
    if (j==N)    //用if判断每种情况都尝试去做，而不用if...else判断
    {
        dp[i+][nex]+=dp[i][state];
        return;
    }
    <<j)&state)>)
        dfs(i,j+,state,nex);    //如果这个位置已经被上一列所占用,直接跳过
    <<j)&state)==)
        dfs(i,j+,state,nex|(<<j));       //如果这个位置是空的，尝试放一个左右覆盖1*2的木板
    <N && ((<<j)&state)== && ((<<(j+))&state)==)
        dfs(i,j+,state,nex);     //如果这个位置以及下一个位置都是空的，尝试放一个上下覆盖2*1的木板，而此时要跳过下一个木块
    return;
}
int main()
{
    while (cin>>N>>M)
    {
        memset(dp,,sizeof(dp));
        dp[][]=;    //初始化第一列状态为0的方法数等于1
        ;i<=M;i++)    //外层for循环遍历每一列
        {
            ;j<(<<N);j++)    //内层for遍历每一个列的所有状态
                if (dp[i][j])    //只要dp[i][j]方法数不为空，就执行dfs方法
                {
                    dfs(i,,j,);
                }
        }
        cout<<dp[M+][]<<endl;    //最后dp[m+1][0]就是结果
    }
}

https://blog.csdn.net/harrypoirot/article/details/23163485

一个大佬讲的状压dp