HDU 5434 Peace small elephant 状压dp+矩阵快速幂

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=5434

Peace small elephant

 Accepts: 38

 Submissions: 108

 Time Limit: 10000/5000 MS (Java/Others)

 Memory Limit: 65536/65536 K (Java/Others)

问题描述

小明很喜欢国际象棋，尤其喜欢国际象棋里面的大象(只要无阻挡能够斜着走任意格)，但是他觉得国际象棋里的大象太凶残了，于是他想到了小象，
小象就没有大象那么凶残，它的攻击范围是它当前格子直角所斜对的格子。现在小明要在棋盘上放很多个小象，有趣的是，当两个小象所在格子有公共边时，
它们将合体变成合体象，多个小象满足条件也会合体，合体象的攻击范围也是它所覆盖格子区域直角所斜对的格子，现在要求任何一个象的攻击范围上是空的(即不摆放棋子)，
小明的棋盘很特殊，有m*nm∗n个格子，求满足条件的摆放的方案数，由于方案数太大，需要对10000000071000000007取模。
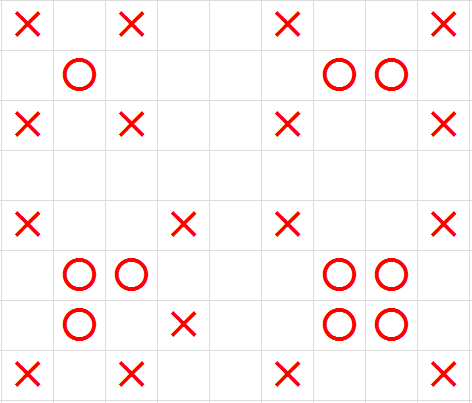
下面给出几种形状下的象的攻击范围图，叉号表示攻击范围。

输入描述

输入有多组数据(最多55组)，每组数据有两个整数n,mn,m含义如题目描述。
1 \leq m \leq 7,1 \leq n \leq 10000000001≤m≤7,1≤n≤1000000000

输出描述

每组数据对应输出一行包含一个整数,表示满足条件的摆放的方案数。

输入样例

1 1
2 3

输出样例

2
50

题解：

　　状压dp+矩阵快速幂。

　　由于m很小，我们考虑将每一列m行的状态压缩成一行，这一行对应的状态总数就是2^m种（m=7时，即：0000000~1111111）。

　　接下来我们求一个矩阵mat[i][j]，代表状态i和状态j是否冲突（比如说0000000和1111111不冲突，而1000000和0100000则冲突）。

如果坐标（i,j），（i+1,j+1）存在小象，那么必须保证（i+1,j)，（i，j+1)两个位置至少有一个棋子，按照这个规则，就能提前得到状态转移矩阵mat了。

　　然后我们要一列一列的往棋盘上放棋子了（注意这时候棋盘已经状压成1*n了，是线性结构，而不是二维结构），由于我们已经得到转移矩阵mat[1<<m][1<<m]了，初始向量vec[1<<m]为全1（因为第一列所有的(1<<m)种状态都不会发生冲突，所以为全1）。我们的任务就是要求：

　　mat^(n-1)*vec （mat^(n-1)表示做n-1次的矩阵乘）

　　由于n非常大，所以我们需要用矩阵快速幂来求mat^(n-1)；

　　总的时间复杂度为 o( (2^m)*(2^m)*(2^m)*(logn) )=o(3e6)

代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;

 const int maxn = ;
 const int mod = ;

 typedef long long LL;

 struct Matrix {
     int n, m;
     int val[maxn][maxn];
     Matrix(int n,int m) :n(n),m(m) {}
     Matrix() {}
     void init(int n, int m) { this->n = n; this->m = m; }
     //把向量看作是n*1的矩阵，所以不用考虑矩阵*向量的情况了。
     friend Matrix operator * (const Matrix& mat1, const Matrix& mat2) {
         Matrix ret(mat1.n, mat2.m);
         for (int i = ; i < ret.n; i++) {
             for (int j = ; j < ret.m; j++) {
                 ret.val[i][j] = ;
                 for (int k = ; k < mat1.m; k++) {
                     ret.val[i][j] += (LL)mat1.val[i][k] * mat2.val[k][j]%mod;
                     ret.val[i][j] %= mod;
                 }
             }
         }
         return ret;
     }
 };

 //矩阵快速幂
 void power(Matrix& mat, int n, Matrix& ans) {
     while (n > ) {
         if (n % ) ans = mat*ans;
         mat = mat*mat;
         n /= ;
     }
 }

 int _n, m;

 //判断状态s1和状态s2是否冲突。
 bool isOk(int s1, int s2) {
     for (int i = ; i<m; i++) {
         if ((s1&( << i)) && !(s2&( << i))) {
             int j;
             j = i - ;
             if (j >= ) {
                 if ((s2&( << j)) && !(s1&( << j))) return false;
             }
             j = i + ;
             if (j<m) {
                 if ((s2&( << j)) && !(s1&( << j))) return false;
             }
         }
     }
     return true;
 }

 Matrix mat, ans;

 void init() {
     mat.init( << m,  << m);
     for (int i = ; i<mat.n; i++) {
         for (int j = ; j<mat.m; j++) {
             if (isOk(i, j)) mat.val[i][j] = ;
             else mat.val[i][j] = ;
         }
     }
     ans.init( << m, );
     for (int i = ; i < ans.n; i++) ans.val[i][] = ;
 }

 int main() {
     while (scanf("%d%d", &_n, &m) ==  && _n) {
         init();
         power(mat, _n - , ans);
         int res = ;
         for (int i = ; i < ans.n; i++) {
             res += ans.val[i][];
             res %= mod;
         }
         printf("%d\n", res);
     }
     return ;
 }