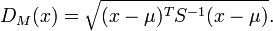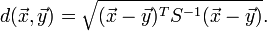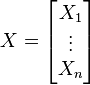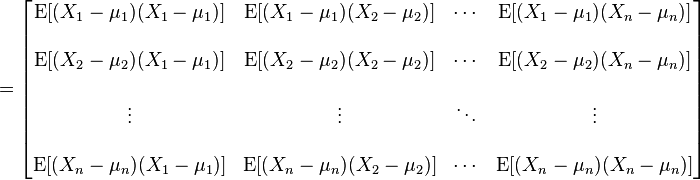paper 114:Mahalanobis Distance(马氏距离)
(from:http://en.wikipedia.org/wiki/Mahalanobis_distance)
Mahalanobis distance
In statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936.It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs fromEuclidean distance in that it takes into account the correlations of the data set and is scale-invariant. In other words, it is a multivariateeffect size.
Definition
Formally, the Mahalanobis distance of a multivariate vector 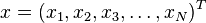 from a group of values with mean
from a group of values with mean 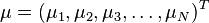 and covariance matrix
and covariance matrix 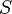 is defined as:
is defined as:
(注:1.这个是X和总体均值的马氏距离。2.这里的S是可逆的,那么协方差矩阵不可逆的话怎么办?)
Mahalanobis distance (or "generalized squared interpoint distance" for its squared value) can also be defined as a dissimilarity measure between two random vectors  and
and  of the same distribution with the covariance matrix
of the same distribution with the covariance matrix 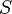 :
:
If the covariance matrix is the identity matrix, the Mahalanobis distance reduces to the Euclidean distance. If the covariance matrix is diagonal, then the resulting distance measure is called the normalized Euclidean distance:
where 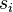 is the standard deviation of the
is the standard deviation of the 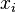 (
(  ) over the sample set.
) over the sample set.
(源自:百度百科)
马氏优缺点:
欧式距离和马氏距离都可以计算两个变量的相似度。
马氏距离能够描述不同维之间的关联性,其关键在于它用到了协方差矩阵,下面是wiki上的介绍:
--------------------------
在统计学与概率论中,协方差矩阵(或称共变异矩阵)是一个矩阵,其每个元素是各个向量元素之间的方差。这是从标量随机变量到高维度随机向量的自然推广。
假设X是以n个标量随机变量组成的列向量(一个列向量代表一个变量,而不是一个记录),
并且μi 是其第i个元素的期望值, 即, μi = E(Xi)。协方差矩阵被定义的第i,j项是如下协方差:
即:
矩阵中的第(i,j)个元素是Xi与Xj的协方差。这个概念是对于标量随机变量方差的一般化推广。
尽管协方差矩阵很简单,可它却是很多领域里的非常有力的工具。它能导出一个变换矩阵,这个矩阵能使数据完全去相关(decorrelation)。从不同的角度看,也就是说能够找出一组最佳的基以紧凑的方式来表达数据。(完整的证明请参考瑞利商)。 这个方法在统计学中被称为主成分分析(principal components analysis),在图像处理中称为Karhunen-Loève 变换(KL-变换)。
-----------------------------------
马氏距离是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。 对于一个均值为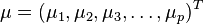 协方差矩阵为Σ的多变量向量
协方差矩阵为Σ的多变量向量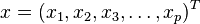 ,其马氏距离为
,其马氏距离为
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量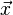 与
与 的差异程度:
的差异程度:
如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧式距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离'.
其中σi 是 xi 的标准差.
http://www.360doc.com/content/10/0804/20/1202138_43697183.shtml
http://people.revoledu.com/kardi/tutorial/Similarity/MahalanobisDistance.html
paper 114:Mahalanobis Distance(马氏距离)的更多相关文章
- Mahalanobis Distance(马氏距离)
(from:http://en.wikipedia.org/wiki/Mahalanobis_distance) Mahalanobis distance In statistics, Mahalan ...
- Mahalanobia Distance(马氏距离)的解释
马氏距离有多重定义: 1)可以表示 某一个样本与DataSet的距离. 2)可以表示两个DataSet之间的距离. 1) The Mahalanobis distance of an observat ...
- 马氏距离(Mahalanobis distance)
马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离.它是一种有效的计算两个未知样本集的相似度的方法.与欧 ...
- MATLAB求马氏距离(Mahalanobis distance)
MATLAB求马氏距离(Mahalanobis distance) 作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 1.马氏距离计算公式 d2(xi, ...
- Mahalanobis距离(马氏距离)的“哲学”解释
讲解教授:赵辉 (FROM : UESTC) 课程:<模式识别> 整理:PO主 基础知识: 假设空间中两点x,y,定义: 欧几里得距离, Mahalanobis距离, 不难发现,如果去掉马 ...
- 有关马氏距离和hinge loss的学习记录
关于度量学习,之前没有看太多相关的文献.不过南京的周老师的一篇NIPS,确实把这个问题剖析得比较清楚. Mahalanobis距离一般表示为d=(x-y)TM(x-y),其中x和y是空间中两个样本点, ...
- 基于欧氏距离和马氏距离的异常点检测—matlab实现
前几天接的一个小项目,基于欧氏距离和马氏距离的异常点检测,已经交接完毕,现在把代码公开. 基于欧式距离的: load data1.txt %导入数据,行为样本,列为特征 X=data1; %赋值给X ...
- Python实现的计算马氏距离算法示例
Python实现的计算马氏距离算法示例 本文实例讲述了Python实现的计算马氏距离算法.分享给大家供大家参考,具体如下: 我给写成函数调用了 python实现马氏距离源代码: # encod ...
- Levenshtein Distance莱文斯坦距离算法来计算字符串的相似度
Levenshtein Distance莱文斯坦距离定义: 数学上,两个字符串a.b之间的莱文斯坦距离表示为levab(|a|, |b|). levab(i, j) = max(i, j) 如果mi ...
随机推荐
- css基础2
标准流(normalflow) ◆元素默认的显示方式都是按照标准流的方式显示 ◆块级元素默认独占一行显示===>标准流显示方式 ◆行内元素在一行上显示===> 标准流的显示方式 浮动 ...
- IOS_ios逆向工程-静态分析
返回博客列表 原 ios逆向工程-静态分析 余成海 发布时间: 2014/11/03 19:17 阅读: 11201 收藏: 17 点赞: 5 评论: 6 最近在学习IOS逆向工程,查看网络上的资料也 ...
- React native 的弹出层(输入)效果
/*弹出层测试*/ import React,{Component} from 'react'; import { StyleSheet, View, Image, Text, TouchableOp ...
- R中一切都是vector
0.可以说R语言中一切结构体的基础是vector! R中一切都是vector,vecotor的每个component必须类型一致(character,numeric,integer....)!vect ...
- iostat命令学习
iostat命令主要用于监控linux系统下cup和磁盘IO的统计信息 可以通过iostat --help获得该命令的帮助信息 [oracle@std ~]$ iostat --help Usage: ...
- ubuntu实现ramdisk
1. linux内核提供了16个ramdisk供使用者使用,只需格式化,并挂在便可以使用.查看 ls /dev/ram* 2. 修改配置文件: sudo gedit /etc/default/grub ...
- Elasticsearch 运维实战之1 -- 集群规划
规划一个可用于生产环境的elasticsearch集群. 集群节点划分 整个集群的节点分为以下三种主要类型 Master nodes -- 负责维护集群状态,不保存index数据, 硬件要求: 一般性 ...
- Ant和Maven的作用是什么?两者之间功能、特点有哪些区别?
Ant和Maven都是基于Java的构建(build)工具.理论上来说,有些类似于(Unix)C中的make ,但没有make的缺陷. Ant是软件构建工具,Maven的定位是软件项目管理和理解工具. ...
- 模拟jquery的$()选择器的实现
<html> <head> </head> <body> <div id="div1">div1</div> ...
- 神奇的 CURL 命令
CURL? 嗯,说来话长了~~~~ 这东西现在已经是苹果机上内置的命令行工具之一了,可见其魅力之一斑 1) 二话不说,先从这里开始吧! curl http: //www.yahoo.com 回车之 ...