【洛谷比赛】[LnOI2019]长脖子鹿省选模拟赛 T1 题解

　　今天是[LnOI2019]长脖子鹿省选模拟赛的时间，小编表示考的不怎么样，改了半天也只会改第一题，那也先呈上题解吧。

T1：P5248 [LnOI2019SP]快速多项式变换(FPT)

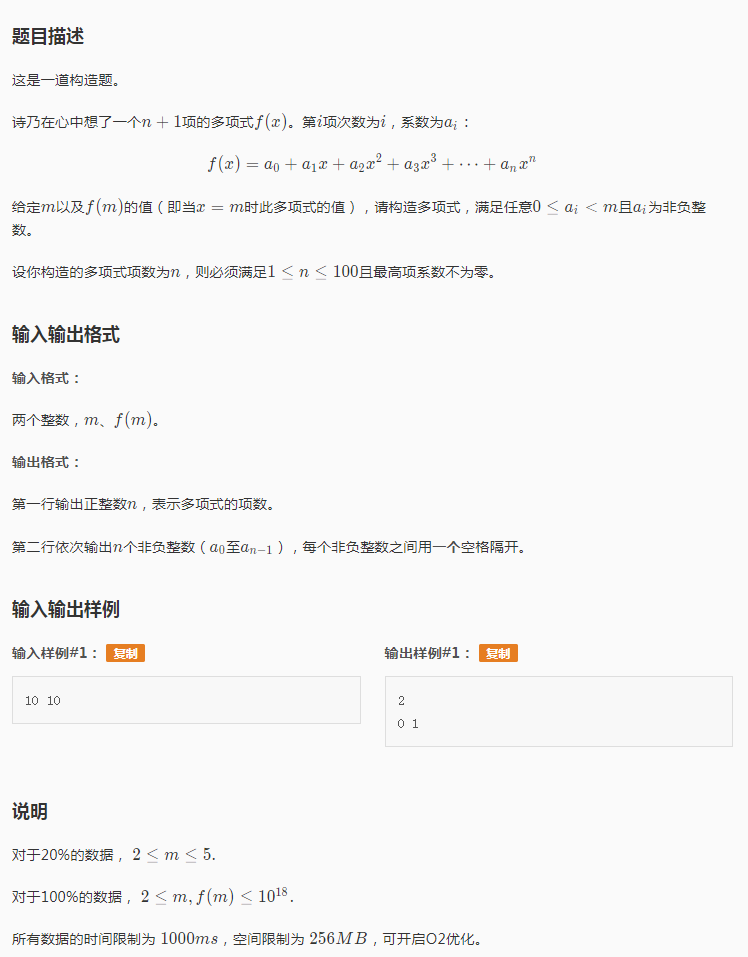
　　一看这题就很手软，没有告诉具体多项式到底有多少项，只好一个一个暴力枚举，但是这也不现实，于是小编就开始骗分，还一分也没骗着。赛后小编看到的题解，才明白这是一道转进制的题，将十进制转换成m进制，m^0,m^1,m^2这不刚好对应上m进制的单位吗？所得结果刚好就是问题的解。那么用短除法模拟算出m进制下f（m）的每一位，输出即可，代码如下：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 int m,f,a[],k=;
 int main()
 {
     scanf("%d%d",&m,&f);
     //cin>>m>>f;
     for(int i=;;i++)
     {
         a[++k]=f%m;
         f/=m;
         if(f==) break;

     }
     printf("%d \n",k);
     //cout<<k<<endl;
     for(int i=;i<=k;i++)
     printf("%d ",a[i]);
     //cout<<a[i]<<" ";
     return ;
 }

　　随便一写发现wa了一大片。

　　进过深思熟虑后发现忘了注意数据规模：

　　10^18，int不爆才怪呢，匆匆一改就过了。

 // luogu-judger-enable-o2
 #include<iostream>
 #include<cstdio>
 using namespace std;
 unsigned long long m,f,a[],k=;
 int main()
 {
     scanf("%lld%lld",&m,&f);
     //cin>>m>>f;
     for(int i=;;i++)
     {
         a[++k]=f%m;
         f/=m;
         if(f==) break;

     }
     printf("%lld \n",k);
     //cout<<k<<endl;
     for(int i=;i<=k;i++)
     printf("%lld ",a[i]);
     //cout<<a[i]<<" ";
     return ;
 }

　　T2，T3，T4的题解小编后续也会加进来……