JAVA数据结构--AVL树的实现

AVL树的定义

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

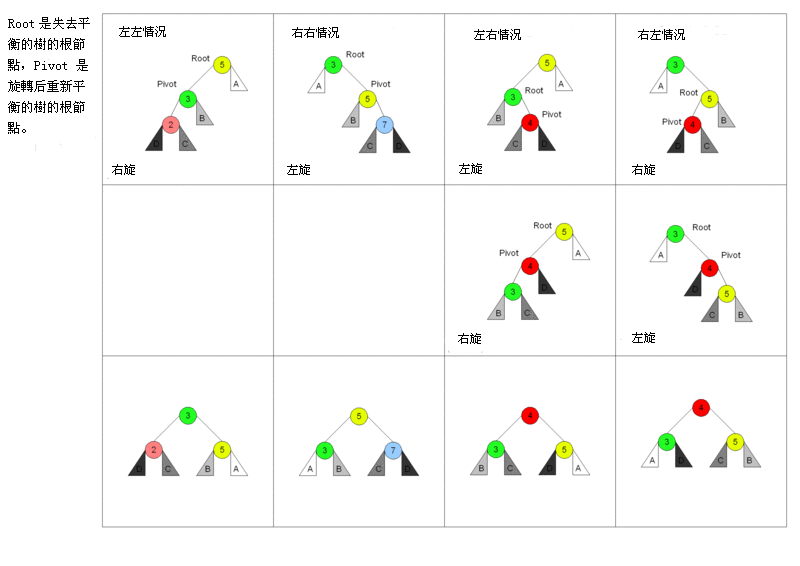
　　上图是摘自维基百科的AVL树实现的图例，比较清晰的解释了AVL调整平衡的过程。ABCD代表当前节点有子树。

　　我以我个人理解以左右情况为例

　　该例是左右情况，需要将其调整为左左或者右右才能继续调整。因为节点5是在右，所以3节点（虚线方框内）调整为左为最佳。左旋转即可使树变为左左形状。

AVL树节点定义

 private static class AvlNode<T>{
         public AvlNode(T theElement) {
             this(theElement, null, null);
         }
         public AvlNode(T theElement,AvlNode<T> lt,AvlNode<T> rt) {
             element=theElement;
             left=lt;
             right=rt;
             height=0;
         }
         T element;
         AvlNode<T> left;
         AvlNode<T> right;
         int height;
     }

与二叉查找树的定义类似，不过加入了节点的深度height定义。

AVL节点计算方法

 private int height(AvlNode<T> t) {
         return t==null?-1:t.height;
 }

当banlance()或者旋转时height都会改变

节点旋转

 /*
      * 实现单旋转
      * */
     private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2){//单左旋转
         AvlNode<T> k1=k2.left;
         k2.left=k1.right;
         k1.right=k2;
         k2.height=Math.max(height(k2.left), height(k2.right))+1;
         k1.height=Math.max(height(k1.left), k2.height)+1;
         return k1;
     }
     private AvlNode<T> rotateWithRightChild(AvlNode<T> k1){//单右旋转
         AvlNode<T> k2=k1.right;
         k1.right=k2.left;
         k2.left=k1;
         k2.height=Math.max(height(k1.left), height(k1.right))+1;
         k1.height=Math.max(height(k2.right), k1.height)+1;
         return k2;
     }
     /*
      * 实现双旋转
      *
      * */
     private AvlNode<T> doubleWithLeftChild(AvlNode<T> k3){//先右旋转再左旋转
         k3.left=rotateWithRightChild(k3.left);
         return rotateWithLeftChild(k3);
     }
      private AvlNode<T> doubleWithRightChild( AvlNode<T> k1 ){//先左旋转再右旋转
          k1.right = rotateWithLeftChild( k1.right );
          return rotateWithRightChild( k1 );
     }

balance()方法的实现

 private AvlNode<T> balance(AvlNode<T> t){
         if(t==null)
             return t;
         if(height(t.left)-height(t.right)>ALLOWED_IMBALANCE) {//左子树高度过高
             if(height(t.left.left)>=height(t.left.right))//判断进行单旋转还是双旋转
                 t=rotateWithLeftChild(t);
             else
                 t=doubleWithLeftChild(t);
         }
         else if (height(t.right)-height(t.left)>ALLOWED_IMBALANCE) {//右子树高度过高
             if(height(t.right.right)>=height(t.right.left))

                 t=rotateWithRightChild(t);
             else
                 t=doubleWithRightChild(t);
         }
         t.height=Math.max(height(t.left), height(t.right))+1;
         return t;
     }

删除节点方法

 private AvlNode<T> remove(T x,AvlNode<T> t){
          if(t==null)
              return t;
          int compareResult=x.compareTo(t.element);
          if(compareResult<0)
              t.left=remove(x, t.left);//递归查找删除
          else if (compareResult>0) {
             t.right=remove(x, t.right);
         }
          else if (t.left!=null&&t.right!=null) {//要删除的节点两个孩子节点的情况
              t.element=findMin(t.right).element;//从右子树中找出最小的节点替换当前要删除的节点
              t.right=remove(t.element, t.right);//删除右子树中需要拿出替换的节点
         }
          else {
             t=(t.left!=null)?t.left:t.right;//单个子节点的情况
         }
          return balance(t);
      }

完整代码如下（不含遍历），github地址

 package Tree;
 public class AvlTree <T extends Comparable<? super T>>{
     private static class AvlNode<T>{
         public AvlNode(T theElement) {
             this(theElement, null, null);
         }
         public AvlNode(T theElement,AvlNode<T> lt,AvlNode<T> rt) {
             element=theElement;
             left=lt;
             right=rt;
             height=0;
         }
         T element;
         AvlNode<T> left;
         AvlNode<T> right;
         int height;
     }
     private AvlNode<T> root;//定义根节点
     public AvlTree() {
         root=null;
     }
     public int height() {
         return height(root);
     }
     public void insert(T x) {
         insert(x, root);
     }
     public void remove(T x) {
         root=remove(x,root);
     }
     private int height(AvlNode<T> t) {
         return t==null?-1:t.height;
     }
     private AvlNode<T> insert(T x,AvlNode<T> t){
         if(t==null)
             return new AvlNode<T>(x, null, null);
         int compareResult=x.compareTo(t.element);
         if(compareResult<0) {
             t.left=insert(x, t.left);
         }
         else if(compareResult>0){
             t.right=insert(x, t.right);
         }
         else {

         }
         return balance(t);

     }
     private AvlNode<T> balance(AvlNode<T> t){
         if(t==null)
             return t;
         if(height(t.left)-height(t.right)>ALLOWED_IMBALANCE) {//左子树高度过高
             if(height(t.left.left)>=height(t.left.right))//判断进行单旋转还是双旋转
                 t=rotateWithLeftChild(t);
             else
                 t=doubleWithLeftChild(t);
         }
         else if (height(t.right)-height(t.left)>ALLOWED_IMBALANCE) {//右子树高度过高
             if(height(t.right.right)>=height(t.right.left))

                 t=rotateWithRightChild(t);
             else
                 t=doubleWithRightChild(t);
         }
         t.height=Math.max(height(t.left), height(t.right))+1;
         return t;
     }
     /*
      * 实现单旋转
      * */
     private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2){//单左旋转
         AvlNode<T> k1=k2.left;
         k2.left=k1.right;
         k1.right=k2;
         k2.height=Math.max(height(k2.left), height(k2.right))+1;
         k1.height=Math.max(height(k1.left), k2.height)+1;
         return k1;
     }
     private AvlNode<T> rotateWithRightChild(AvlNode<T> k1){//单右旋转
         AvlNode<T> k2=k1.right;
         k1.right=k2.left;
         k2.left=k1;
         k2.height=Math.max(height(k1.left), height(k1.right))+1;
         k1.height=Math.max(height(k2.right), k1.height)+1;
         return k2;
     }
     /*
      * 实现双旋转
      *
      * */
     private AvlNode<T> doubleWithLeftChild(AvlNode<T> k3){//先右旋转再左旋转
         k3.left=rotateWithRightChild(k3.left);
         return rotateWithLeftChild(k3);
     }
      private AvlNode<T> doubleWithRightChild( AvlNode<T> k1 ){//先左旋转再右旋转
          k1.right = rotateWithLeftChild( k1.right );
          return rotateWithRightChild( k1 );
     }
      private AvlNode<T> remove(T x,AvlNode<T> t){
          if(t==null)
              return t;
          int compareResult=x.compareTo(t.element);
          if(compareResult<0)
              t.left=remove(x, t.left);//递归查找删除
          else if (compareResult>0) {
             t.right=remove(x, t.right);
         }
          else if (t.left!=null&&t.right!=null) {//要删除的节点两个孩子节点的情况
              t.element=findMin(t.right).element;//从右子树中找出最小的节点替换当前要删除的节点
              t.right=remove(t.element, t.right);//删除右子树中需要拿出替换的节点
         }
          else {
             t=(t.left!=null)?t.left:t.right;//单个子节点的情况
         }
          return balance(t);
      }
      private AvlNode<T> findMin(AvlNode<T> t){
             //非递归写法
             if(t!=null)
                 while(t.left!=null)
                     t=t.left;
             return t;
             //递归写法
             /*if(t==null)
                 return null;
             else if (t.left==null) {
                 return t;
             }
             return findMin(t.left);*/
         }
     private static final int ALLOWED_IMBALANCE=1;

 }