codeforces 85D D. Sum of Medians Vector的妙用

D. Sum of Medians

Time Limit: 1 Sec  Memory Limit: 256 MB

题目连接

http://codeforces.com/problemset/problem/85/D

Description

In one well-known algorithm of finding the k-th order statistics we should divide all elements into groups of five consecutive elements and find the median of each five. A median is called the middle element of a sorted array (it's the third largest element for a group of five). To increase the algorithm's performance speed on a modern video card, you should be able to find a sum of medians in each five of the array.

A sum of medians of a sorted k-element set S = {a₁, a₂, ..., a_k}, where a₁ < a₂ < a₃ < ... < a_k, will be understood by as

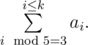
The 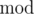operator stands for taking the remainder, that is 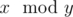stands for the remainder of dividing x by y.

To organize exercise testing quickly calculating the sum of medians for a changing set was needed.

Input

The first line contains number n (1 ≤ n ≤ 10⁵), the number of operations performed.

Then each of n lines contains the description of one of the three operations:

• add x — add the element x to the set;
• del x — delete the element x from the set;
• sum — find the sum of medians of the set.

For any add x operation it is true that the element x is not included in the set directly before the operation.

For any del x operation it is true that the element x is included in the set directly before the operation.

All the numbers in the input are positive integers, not exceeding 10⁹.

 

Output

For each operation sum print on the single line the sum of medians of the current set. If the set is empty, print 0.

Please, do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams (also you may use the %I64d specificator).

 

Sample Input

6
add 4
add 5
add 1
add 2
add 3
sum

Sample Output

3

HINT

题意

给你一堆数，然后排序，然后让你输出下标mod5=3的和

题解：

用vector来做，虽然感觉有很多数据结构都可以把这道题秒了

代码：

//qscqesze
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 200001
#define mod 10007
#define eps 1e-9
int Num;
char CH[];
//const int inf=0x7fffffff;   //нчоч╢С
const int inf=0x3f3f3f3f;
/*

inline void P(int x)
{
    Num=0;if(!x){putchar('0');puts("");return;}
    while(x>0)CH[++Num]=x%10,x/=10;
    while(Num)putchar(CH[Num--]+48);
    puts("");
}
*/
//**************************************************************************************
inline ll read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
inline void P(int x)
{
    Num=;if(!x){putchar('');puts("");return;}
    while(x>)CH[++Num]=x%,x/=;
    while(Num)putchar(CH[Num--]+);
    puts("");
}

vector<int> s;
int main()
{
    char a[];
    int b;
    int n=read();
    for(int i=;i<n;i++)
    {
        scanf("%s",a);
        if(a[]=='a')
        {
            scanf("%d",&b);
            s.insert(lower_bound(s.begin(),s.end(),b),b);
        }
        if(a[]=='d')
        {
            scanf("%d",&b);
            s.erase(lower_bound(s.begin(),s.end(),b));
        }
        if(a[]=='s')
        {
            ll sum=;
            for(int j=;j<s.size();j+=)
                sum+=s[j];
            printf("%lld\n",sum);
        }
    }
}