数据降维PCA——学习笔记

PCA主成分分析

无监督学习

使方差（数据离散量）最大，更易于分类。

可以对隐私数据PCA，数据加密。

基变换

投影->内积

基变换

正交的基，两个向量垂直（内积为0，线性无关）

先将基化成各维度下的单位向量。

一般把数据写成列向量的形式，新的基写成矩阵的形式。

基×向量

R个基向量，行向量表示。R维空间内，p1...pr。p是行向量。

m个样本，m列。n个特征。

将右面矩阵内每一个列向量（样本），映射到R维空间内

原来可能有n个特征，现在变成了R个特征。m个样本：

基的选择

尽可能保留原来信息，但又更离散（方差大），易于分类。

二维的数据点，投影到一维。寻找方差最大的方向。

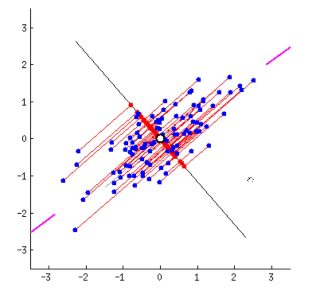
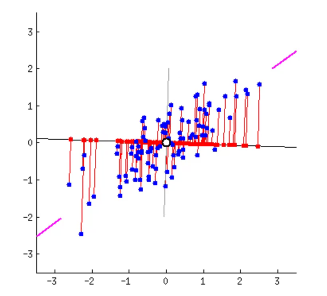
可以发现，第二个图中，刚好直线上投影点更离散。

协方差

先会对数据中心化，变成均值为0。即类似方差中的μ=0。a^2->a

m个样本

协方差矩阵同时包含了方差和协方差。
希望方差最大，协方差最小。

最大的特征值对应的特征向量，就是方差最大。选前k个最大的，k个单位向量->最好的k个基

实例

二维,5个样本

降到一维,选一个c1

两个特征向量,一定是可以把协方差矩阵对角化.