R与数据分析旧笔记（一）基本数学函数的使用
创建向量矩阵
> x1=c(2,3,6,8)
> x2=c(1,2,3,4)
> a1=(1:100)
> length(a1)
[1] 100
> length(x1)
[1] 4
> mode(x1)
[1] "numeric"
> rbind(x1,x2)
[,1] [,2] [,3] [,4]
x1 2 3 6 8
x2 1 2 3 4
> cbind(x1,x2)
x1 x2
[1,] 2 1
[2,] 3 2
[3,] 6 3
[4,] 8 4
求平均值，和，连乘，最值，方差，标准差
> mean(x1) [1] 4.75 > sum(x1) [1] 19 > max(x1) [1] 8 > min(x1) [1] 2 > var(x1) [1] 7.583333 > prod(x1) [1] 288 > sd(x1) [1] 2.753785
产生向量
> 1:10 [1] 1 2 3 4 5 6 7 8 9 10 > 1:10-1 [1] 0 1 2 3 4 5 6 7 8 9 > 1:10*2 [1] 2 4 6 8 10 12 14 16 18 20 > a=2:60*2+1 > a [1] 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 [20] 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 [39] 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 [58] 119 121 > a[5] [1] 13 > a[-5] [1] 5 7 9 11 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 [20] 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 [39] 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 [58] 121 > a[c(2,3,8)] [1] 7 9 19 > a[a<20] [1] 5 7 9 11 13 15 17 19 > a[a[3]] [1] 21 > seq(6,20) [1] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > seq(5,121,by=2) [1] 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 [20] 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 [39] 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 [58] 119 121 > seq(5,121,length=10) [1] 5.00000 17.88889 30.77778 43.66667 56.55556 69.44444 82.33333 [8] 95.22222 108.11111 121.00000
新建向量
> a=c(2,3,4,2,3,2,1,4,3,2,1) > which.max(a) [1] 3 > a[which.max(a)] [1] 4 > which(a==2) [1] 1 4 6 10 > a[which(a==2)] [1] 2 2 2 2 > which(a>5) integer(0) > a[which(a>5)] numeric(0) > a=1:20 > a [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > rev(a) [1] 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 > a=c(2,3,4,5,6,6,7,8,3,2) > sort(a) [1] 2 2 3 3 4 5 6 6 7 8 > rev(sort(a)) [1] 8 7 6 6 5 4 3 3 2 2
生成矩阵
> a1=c(1:12)
> matrix(a1,nrow=3,ncol=4)
[,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12
> matrix(a1,nrow=4,ncol=3)
[,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12
> matrix(a1,nrow=4,ncol=3,byrow=T)
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
[4,] 10 11 12
矩阵运算
矩阵相加
> a=matrix(1:12,nrow=3,ncol=4)
> t(a)
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
[4,] 10 11 12
> a=b=matrix(1:12,nrow=3,ncol=4)
> a+b
[,1] [,2] [,3] [,4]
[1,] 2 8 14 20
[2,] 4 10 16 22
[3,] 6 12 18 24
> a-b
[,1] [,2] [,3] [,4]
[1,] 0 0 0 0
[2,] 0 0 0 0
[3,] 0 0 0 0
矩阵相乘
> a=matrix(1:12,nrow=3,ncol=4)
> b=matrix(1:12,nrow=4,ncol=3)
> a%*%b
[,1] [,2] [,3]
[1,] 70 158 246
[2,] 80 184 288
[3,] 90 210 330
> a=matrix(1:16,nrow=4,ncol=4)
> a
[,1] [,2] [,3] [,4]
[1,] 1 5 9 13
[2,] 2 6 10 14
[3,] 3 7 11 15
[4,] 4 8 12 16
> diag(a)
[1] 1 6 11 16
> diag(diag(a))
[,1] [,2] [,3] [,4]
[1,] 1 0 0 0
[2,] 0 6 0 0
[3,] 0 0 11 0
[4,] 0 0 0 16
> diag(4)
[,1] [,2] [,3] [,4]
[1,] 1 0 0 0
[2,] 0 1 0 0
[3,] 0 0 1 0
[4,] 0 0 0 1
矩阵求逆
> a=matrix(rnorm(16),4,4)
> a
[,1] [,2] [,3] [,4]
[1,] -1.604650746 -2.22482987 1.5094439 1.0070701
[2,] 0.006409861 -0.01506928 -0.6651050 -1.9342548
[3,] -1.606959408 -0.49430092 -0.9376593 0.1979031
[4,] 0.422441416 -0.33201336 0.3848287 1.1256368
> solve(a)
[,1] [,2] [,3] [,4]
[1,] -0.1426715 0.5944611 -0.1676185 1.1786143
[2,] -0.1804919 -0.9604913 -0.2055298 -1.4528592
[3,] 0.3168603 -0.5776493 -0.6252734 -1.1661647
[4,] -0.1080209 -0.3089139 0.2160497 0.4162172
解线性方程组
> a=matrix(rnorm(16),4,4)> a [,1] [,2] [,3] [,4][1,] -1.604650746 -2.22482987 1.5094439 1.0070701[2,] 0.006409861 -0.01506928 -0.6651050 -1.9342548[3,] -1.606959408 -0.49430092 -0.9376593 0.1979031[4,] 0.422441416 -0.33201336 0.3848287 1.1256368> solve(a) [,1] [,2] [,3] [,4][1,] -0.1426715 0.5944611 -0.1676185 1.1786143[2,] -0.1804919 -0.9604913 -0.2055298 -1.4528592[3,] 0.3168603 -0.5776493 -0.6252734 -1.1661647[4,] -0.1080209 -0.3089139 0.2160497 0.4162172> a=matrix(rnorm(16),4,4)> a [,1] [,2] [,3] [,4][1,] 1.0451867 -0.2426553 -0.51232551 -0.12062549[2,] -1.5518006 -0.1333096 0.03677731 -0.10715366[3,] -1.0620249 -1.3160312 0.01713207 0.09320016[4,] -0.6664664 2.2398778 1.94861889 0.01788447> b=c(1:4)> b[1] 1 2 3 4> solve(a,b)[1] 0.9840158 -4.6924392 8.0064010 -24.3295023
矩阵的特征值与特征向量
> a=diag(4)+1
> a
[,1] [,2] [,3] [,4]
[1,] 2 1 1 1
[2,] 1 2 1 1
[3,] 1 1 2 1
[4,] 1 1 1 2
> a.e=eigen(a,symmetric=T)
> a.e
$values
[1] 5 1 1 1
$vectors
[,1] [,2] [,3] [,4]
[1,] -0.5 0.8660254 0.0000000 0.0000000
[2,] -0.5 -0.2886751 -0.5773503 -0.5773503
[3,] -0.5 -0.2886751 -0.2113249 0.7886751
[4,] -0.5 -0.2886751 0.7886751 -0.2113249
> a.e$vectors%*%diag(a.e$values)%*%t(a.e$vectors)
[,1] [,2] [,3] [,4]
[1,] 2 1 1 1
[2,] 1 2 1 1
[3,] 1 1 2 1
[4,] 1 1 1 2
数据框
> x1=c(10,13,14,23,43) > x2=c(12,35,35,67,54) > x=data.frame(x1,x2) > x x1 x2 1 10 12 2 13 35 3 14 35 4 23 67 5 43 54 > plot(x)#散点图
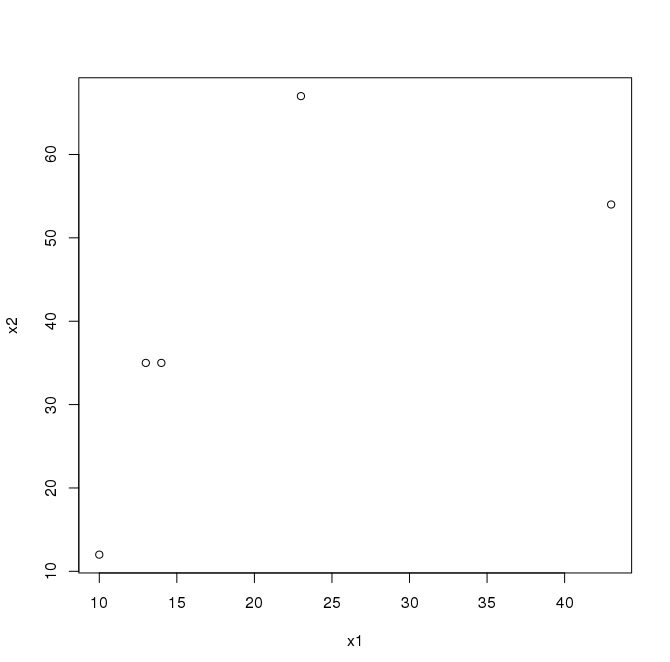
读文本文件
(x=read.table("abc.txt"))
#读剪贴板
y=read.table("clipboard",header=F)
y
z=read.table("clipboard",header=T)
z
循环语句
for语句
> for(i in 1:59) {a[i]=1*2+3}
> a
[1] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
[39] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
>
> b=0
> for(i in 1:59) {a[i]=i*2+3;b[i]=i*5-4}
> b
[1] 1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91
[20] 96 101 106 111 116 121 126 131 136 141 146 151 156 161 166 171 176 181 186
[39] 191 196 201 206 211 216 221 226 231 236 241 246 251 256 261 266 271 276 281
[58] 286 291
while语句
a[1]=5
> i=1
> while(a[i]<121) {i=i+1;a[i]=a[i-1]+2}
> a
[1] 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41
[20] 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79
[39] 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117
[58] 119 121
R脚本引用
source() print()
R与数据分析旧笔记（一）基本数学函数的使用的更多相关文章
- R与数据分析旧笔记（十八完结） 因子分析
因子分析 因子分析 降维的一种方法,是主成分分析的推广和发展 是用于分析隐藏在表面现象背后的因子作用的统计模型.试图用最少的个数的不可测的公共因子的线性函数与特殊因子之和来描述原来观测的每一分量 因子 ...
- R与数据分析旧笔记（五）数学分析基本
R语言的各种分布函数 rnorm(n,mean=0,sd=1)#高斯(正态) rexp(n,rate=1)#指数 rgamma(n,shape,scale=1)#γ分布 rpois(n,lambda) ...
- R与数据分析旧笔记（三）不知道取什么题目
连线图 > a=c(2,3,4,5,6) > b=c(4,7,8,9,12) > plot(a,b,type="l") 多条曲线效果 plot(rain$Toky ...
- R与数据分析旧笔记（十七） 主成分分析
主成分分析 主成分分析 Pearson于1901年提出的,再由Hotelling(1933)加以发展的一种多变量统计方法 通过析取主成分显出最大的个别差异,也用来削减回归分析和聚类分析中变量的数目 可 ...
- R与数据分析旧笔记（十六） 基于密度的方法：DBSCAN
基于密度的方法:DBSCAN 基于密度的方法:DBSCAN DBSCAN=Density-Based Spatial Clustering of Applications with Noise 本算法 ...
- R与数据分析旧笔记（十五） 基于有代表性的点的技术：K中心聚类法
基于有代表性的点的技术:K中心聚类法 基于有代表性的点的技术:K中心聚类法 算法步骤 随机选择k个点作为"中心点" 计算剩余的点到这个k中心点的距离,每个点被分配到最近的中心点组成 ...
- R与数据分析旧笔记（十三） 聚类初步
聚类 聚类 关键度量指标:距离 常用距离 绝对值距离 绝对值距离也称为"棋盘距离"或"城市街区距离". 欧氏(Euclide)距离 闵可夫斯基(Minkowsk ...
- R与数据分析旧笔记（十一）数据挖掘初步
PART 1 PART 1 传统回归模型的困难 1.为什么一定是线性的?或某种非线性模型? 2.过分依赖于分析者的经验 3.对于非连续的离散数据难以处理 网格方法 <Science>上的文 ...
- R与数据分析旧笔记（⑨）广义线性回归模型
广义线性回归模型 广义线性回归模型 例题1 R.Norell实验 为研究高压电线对牲畜的影响,R.Norell研究小的电流对农场动物的影响.他在实验中,选择了7头,6种电击强度, 0,1,2,3,4, ...
随机推荐
- ASP.NET mvc4 WEB API异常处理
当一个web api抛出一个异常后 此异常会被转化成一个HTTP响应 错误代码为500的服务错误 但是如果你不想让客户端看到500的错误码 你也可以自定义错误码 如下代码当用户输入的ID没有与之相关的 ...
- C# 数据库dataGridView刷新数据和主外键判断
本文主要讲诉在使用VS2012+SQL Server数据库做系统中,通常会遇到几个问题.使用dataGridView控件在修改.删除.插入数据后,怎样刷新数据显示操作后的结果.同时在对数据操作时通常会 ...
- 一个tabBarController管理多个Storyboard
随着项目的业务逻辑越来越复杂,随着项目越来越大,那么我们Storybard中得控制器就越来越多, 就越来越难以维护.然而使用Storyborad又能更方便的帮助我们做屏幕适配(PS:尤其在6.6+出来 ...
- 自定义ASP.NET WebApplication中调用SharePoint2010的对象
如果你是做SharePoint开发的话,一定不会对如下这段代码陌生: using(SPSite oSiteCollection = new SPSite("http://Server_Nam ...
- 使用ionic与cordova（phonegap）进行轻量级app开发前的环境配置与打包安卓apk过程记录
前言 有人说:"如果你恨一个人,就让ta去接触cordova(phonegap)",这是因为这里面的水很深,坑很多,真让人不是一般地发狂.或许有幸运的人儿基本顺顺利利就配置完环境 ...
- 场景：A-->B-->C 跳转到C时，要关掉B的处理方法
场景:A-->B-->C 跳转到C时,要关掉B的处理方法:相当于从A跳转到C UIViewController *preController = [self.navigationContr ...
- 20151210--MVC
package com.hanqi; import java.io.IOException; import java.sql.*; import java.text.SimpleDateFormat; ...
- Linux程序设计 读笔2 Shell脚本
第二章 Shell程序设计 四.管道和重定向 1 重定向输出 ls -l > lsoutput.txt ps >> lsoutput.txt >>表示附加到一个文件中 文 ...
- 持续集成 之 apache-continuum
作者:许振坪,http://blog.csdn.net/benkaoya 1.前言 最近在研究持续集成,摸索了很多持续集成的工具,Apache Continuum也包括其中.既然飞过,那就留下点什么吧 ...
- phpcms-v9 前台模板文件中{pc}标签的执行流程
前台pc标签的使用:{pc:content 参数名="参数值" 参数名="参数值" 参数名="参数值"} 如: {pc:content ac ...