[MIT Intro. to algo]Lecture 1: 课程介绍，算法优势，插入算法和归并算法分析，渐近符号

The theoretical study of computer program performance and resource useage.

 

First, analysis and then design.

 

Questions:

1 In programming, what is more important than performance（有什么比性能更重要）?

correctness, simplicity（简洁性）, maintainability, stability, modularity（模块化，避免修改功能以外的代码）, efficiency, programmer's time, security, 

scalability（可扩展性）,  Functionality(特性多), user friendliness （用户友好）

2 why study algorithms and performance?（那为什么还要学习算法？）

user friendliness(提高性能也会用户友好) ，feasible versus infeasible（内存占用多或速度慢会导致不可行）, you can use algorithms to pay for these other things that you want(like user friendilness, security, ).

like communication and memory and so forth，同performance一样需要节约.. for fun.

 

Problem ：Sorting（排序问题）

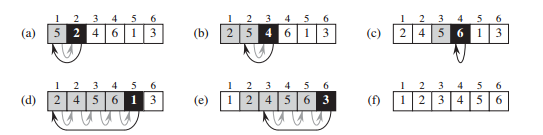
Insertion Sort: move the key and copy to a position to compare if it is corrent

 

Running time:（运行时间）

Depends on input(e.g. already sorted)

Depends on input size(6 elem. vs 6 * 10^9 elem.) -- parametionze in input size

want upper bounds（想知道它运行时间的上限） -- guarantee to user

 

Kinds of anaylysis:（如何分析）

Worst-case(usually): T(n) = max time on any imput of size n

Average-case (sometimes) T(n) = expected time over all inputs of size n（每种输入的概率*时间，求和平均

 -- statistical distribution of inputs(Need assumption of statistic distribution, like normal distr.)

Best-case: (bogus 假象) just for cheat,为特定输入给出特定输出，not for all cases。

 

What is ins-sort's w-c time?

    Depends on computer

        -- relative speed (on same machine) 在相同机器上比较相对速度

        -- absolute sppeed (on diff machine) 真的会有某个算法不关在什么计算机上运行都最快吗？这会很困惑

 

BIG IDEA:

Asymtotic analysis: 渐近分析

1 Ignore machine dependent constants（忽略与机器相关的常量）

2 look at growth of T(n) as n - > infinity

 

Asymptotic notation(渐近符号)

theta-notation： drop lowner order terms Ignore leading constants

    Ex: 3n^3 + 90n^2 -5n -6046 = theta(n^3)

As n-> infinity , theta(n^2) alg. always beats a theta(n^3) alg.（即使在不同的机器上，极其差别也只是constants diff）

会由一个点开始，theta(n^2)与theta(n^3)消耗相同或更少

 

Insertion Sort:（插入排序）

 

T(n) = 求和（j = 2-> n）:theta(j) = theta(n^2)(arithmetic serias算数级数)

 

Is insertion sort fast?

    -- moderately so, for small n（对于很小的n，适度的快）

    -- not at all for largen

 

Merge Sort:（归并排序）

 

 

    1 If n == 1,  done                                                     (theta(1))

    2 Recursively sort: A[1... n/2] and A[(n/2+1) ... n]    (2T(n/2))

    3 Merge two sorted list                                            (theta(n))

 

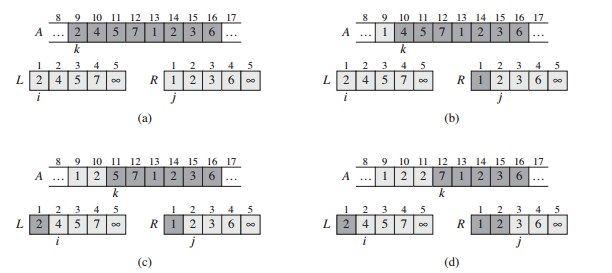
Key subroutine is Merge:（子集合并）

两个子列，20 13 7 2， 12 11 9 1， 两个列中的最小值比较，拿走1，在比较两个列中的最小值，拿走2，当某一个子列空了，另一个子列整个拿走。操作数是固定的，因此：

Time = theta(n) on n total elems. 在下面即为c*n

 

T(n) = theta(1), if n = 1 (usually omit)

T(n) = 2T(n/2) + theta(n) if n > 1

 

Recrusion tree:（递归树）

　　　　　　   T(n) = 2T(n/2) +c*n (c is a contant) 可以写成树状：（高度是lgn， 叶子数为n）

                                =  2(2T(n/4) + c*n/2)) + c*n

                                = ... 

                                = lgn个c*n以及叶子上的n个theta(1)，即为theta(n))

                                = c*n*lgn+ theta(n)

                                = theta(n*lgn)（去掉低阶项）

 

Result: theta(n*lgn) is faster then theta(n^2) when the element size is larger than a number.