洛谷P1288 取数游戏II[博弈论]

题目描述

有一个取数的游戏。初始时，给出一个环，环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后，将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏，两人轮流取数，取数的规则如下：

（1）选择硬币左边或者右边的一条边，并且边上的数非0；

（2）将这条边上的数减至任意一个非负整数(至少要有所减小)；

（3）将硬币移至边的另一端。

如果轮到一个玩家走，这时硬币左右两边的边上的数值都是0，那么这个玩家就输了。

如下图，描述的是Alice和Bob两人的对弈过程，其中黑色节点表示硬币所在节点。结果图(d)中，轮到Bob走时，硬币两边的边上都是0，所以Alcie获胜。

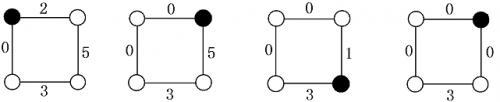
（a）Alice （b）Bob （c）Alice （d）Bob

现在，你的任务就是根据给出的环、边上的数值以及起点（硬币所在位置），判断先走方是否有必胜的策略。

输入输出格式

输入格式：

第一行一个整数N（N≤20），表示环上的节点数。

第二行N个数，数值不超过30，依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。

输出格式：

仅一行。若存在必胜策略，则输出“YES”，否则输出“NO”。

输入输出样例

输入样例#1：

【输入1】
4
2 5 3 0
【输入2】
3
0 0 0

输出样例#1：

【输出1】
YES
【输出2】
NO

---

至少有1个0
先从简单情况找一下规律
可以发现取0是逼着对手往另一条边走
如果到0经过奇数条边Alice就赢了

#include <cstdio>
const int N=;
int n,a[N];
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++) scanf("%d",&a[i]);
    int x=,y=;
    for(int i=;i<=n&&a[i]!=;i++) x++;
    for(int i=n;i>=&&a[i]!=;i--) y++;
    if((x&)||(y&)) puts("YES");
    else puts("NO");
}