C++ 简单介绍线段树

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上k。
2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数n,m分别表示该数列数字的个数和操作的总个数。

第二行包含n个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来m行每行包含3或4个整数，表示一个操作，具体如下：

1. 1 x y k：将区间[x,y]内的数每个加上k。
2. 2 x y：输出区间[x,y]内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1 复制

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出 #1 复制

11
8
20

说明/提示

保证任意时刻数列中任意元素的和在[-2^63,2^63)内。

对于100%的数据，1<=n,m<=10^5。

【样例解释】

这是一个经典的线段树，曾经让我满脸懵逼的算法，但是真的很好用。（虽然代码有点长）今天我讲讲自己的理解，希望能帮到不会的同学。

一张烂到不能再烂的图片：

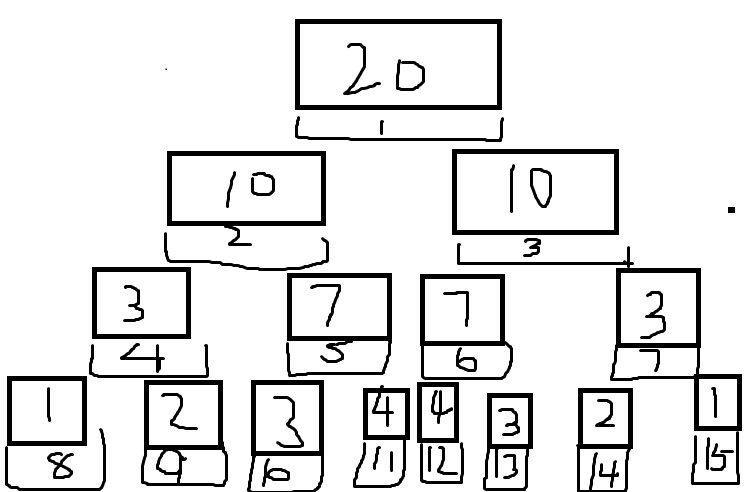
这张图片的最低层就是原数组，每个方块下面的数组就是在线段树数组中的位置。先从1开始，如果现在的位置是一个点，就返回这个点的值，否则继续向下查找，然后把这个点的值设定为他左右儿子的和。

一个神奇的操作：

void build(long long int l,long long int r,long long int k)
{
	tree[k].l=l;//tree是线段树数组，l和r分别是左右点位置。
	tree[k].r=r;
	if(l==r)//如果是同一个点，表示到达叶子节点，该输入了。
	{
		scanf("%lld",&tree[k].zhi);
		return ;
	}
	int mid=(l+r)/2;//分成2段，二分。
	build(l,mid,k*2);//一个位置是k*2
	build(mid+1,r,k*2+1);//一个位置是k*2+1
	tree[k].zhi=tree[k*2].zhi+tree[k*2+1].zhi;//父节点的值相当于2个子节点的和。
}

这就是线段树的初始化。大家可以输出一下tree数组的zhi变量，一定和上图一样，每个节点都等于他的两个子节点。

线段树初始化完了。接下来是查找。

上面的初始化我们让父节点等于他的2个子节点相加，我们就根据这个来求区间查找。具体思想是：如果爸爸超过了范围，就去找儿子，一直向下找，直到找到一个被要求的区间完全包含的后代。然后就把他的值返回，这个方法是绝对不会重复的，因为线段树每层每个节点值只包含在一个空间内。如果爸爸被选择，儿子也就没有必要查下去了。就造就了一个上下层不可能被选，同层不存在重叠的现象。所以这种方法不可能重复。

另外还有一个小小的判断，如果要选区间的开头大于儿子的结尾，或者相反，那这个儿子就没比要查下去了。

说了这么多，该写代码了：

void chazhao(long long int k)//现在的位置
{
	if(tree[k].l>=q&&tree[k].r<=h)//被完全包含，q，h，是要查找区间的开头和结尾
	{
		shu+=tree[k].zhi;//shu是最后的加和。
		return ;
	}
	int mid=(tree[k].l+tree[k].r)/2;//获取子节点的结尾位置。
	if(q<=mid)//开头小于左子节点的结尾，左子节点包含一部分。需要查看。
	{
		chazhao(k*2);
	}
	if(h>mid)//结尾大于右子节点的开头，右子节点包含一部分。需要查看。
	{
		chazhao(k*2+1);
	}
}

　查找和建树都是这么草率。好好理解一下二分就可以写出来。接下来是（我认为）最难的区间修改，他需要用到一个神奇的东西，叫做懒标记，其意差不多是这个区间包含的值全都要加a，那我就先算出自己需要的值，加上。再定义一个变量，告诉他这个以下全部都要+a，然后就不管了……咕咕咕

当然没这么容易结束，我们以一种现在不用死活不动的态度来处理这个a。只有需要用到这个区间的子区间时，才会把标记下传。懒标记的好处就是避免无用操作，用得到再动。可以毫不夸张的说，没来懒标记的线段树，连暴力都不如。

void down(long long int k)
{
	tree[k*2].zhi+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
	tree[k*2].f+=tree[k].f;
	tree[k*2+1].zhi+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
	tree[k*2+1].f+=tree[k].f;
	tree[k].f=0;
	return ;
}

下降函数，当需要查找一个空间的子节点，但这个空间的懒标记没有清空，就会对子节点的操作产生误差。每个值都加上a的话，整个空间增加的量就是（存的长度*a）。然后这个空间需要继承父亲要增加的值。因为他的子节点一样要加。但我们仍然以现在不用死活不动的态度来处理。也就是说，不主动向下传，只有要用的时候再传。

要判断是否要用，就要在每个函数都加一些东西：

if(tree[k].f!=0){//如果懒标记不为0，说明他的子节点没有加上应该加的数，会导致误判，所以向下传承懒标记。
    down(k);
}

如果在查找的时候不包含，就判断。因为他要去下一层了，需要把这一层的懒标记向下移动。

现在就差最后一步，修改。

void xg(long long int k)
{
	if(tree[k].l>=q&&tree[k].r<=h)
    {
        tree[k].zhi+=(tree[k].r-tree[k].l+1)*a;//先改变本身的值
        tree[k].f+=a;//懒标记增加。
        return;
    }
    if(tree[k].f!=0)//要去找儿子，但懒标记还有，向下传。
    {
    	down(k);
    }
    int mid=(tree[k].l+tree[k].r)/2;
    if(q<=mid)
	{
		xg(k*2);
	}
    if(h>mid)
	{
		xg(k*2+1);
	}
    tree[k].zhi=tree[k*2].zhi+tree[k*2+1].zhi;//父节点的值等于左右子节点的和。
    return;
}

好了，现在该上完整的代码了。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cmath>
#include<cstring>
using namespace std;
long long n,shu,q,h,m,a,l,r,a1;
struct hehe
{
	long long l,r,f,w,zhi;
}tree[400005];//数组大小开到n*4比较保险
void build(long long int l,long long int r,long long int k)
{
	tree[k].l=l;//tree是线段树数组，l和r分别是左右点位置。
	tree[k].r=r;
	if(l==r)//如果是同一个点，表示到达叶子节点，该输入了。
	{
		scanf("%lld",&tree[k].zhi);
		return ;
	}
	int mid=(l+r)/2;//分成2段，二分。
	build(l,mid,k*2);//一个位置是k*2
	build(mid+1,r,k*2+1);//一个位置是k*2+1
	tree[k].zhi=tree[k*2].zhi+tree[k*2+1].zhi;//父节点的值相当于2个子节点的和。
}
void down(long long int k)
{
	tree[k*2].zhi+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
	tree[k*2].f+=tree[k].f;
	tree[k*2+1].zhi+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
	tree[k*2+1].f+=tree[k].f;
	tree[k].f=0;
	return ;
}
void chazhao(long long int k)//现在的位置
{
	if(tree[k].l>=q&&tree[k].r<=h)//被完全包含，q，h，是要查找区间的开头和结尾
	{
		shu+=tree[k].zhi;//shu是最后的加和。
		return ;
	}
	if(tree[k].f!=0){//如果懒标记不为0，说明他的子节点没有加上应该加的数，会导致误判，所以向下传承懒标记。
    	down(k);
	}
	int mid=(tree[k].l+tree[k].r)/2;//获取子节点的结尾位置。
	if(q<=mid)//开头小于左子节点的结尾，左子节点包含一部分。需要查看。
	{
		chazhao(k*2);
	}
	if(h>mid)//结尾大于右子节点的开头，右子节点包含一部分。需要查看。
	{
		chazhao(k*2+1);
	}
}
void xg(long long int k)
{
	if(tree[k].l>=q&&tree[k].r<=h)
    {
        tree[k].zhi+=(tree[k].r-tree[k].l+1)*a;
        tree[k].f+=a;
        return;
    }
    if(tree[k].f!=0)
    {
    	down(k);
    }
    int mid=(tree[k].l+tree[k].r)/2;
    if(q<=mid)
	{
		xg(k*2);
	}
    if(h>mid)
	{
		xg(k*2+1);
	}
    tree[k].zhi=tree[k*2].zhi+tree[k*2+1].zhi;
    return;
}
int main()
{
	cin>>n>>m;
	build(1,n,1);
	for(int i=0;i<m;i++)
	{
		scanf("%lld",&a1);
		if(a1==1)
		{
			scanf("%lld%lld%lld",&q,&h,&a);
			xg(1);
		}else if(a1==2)
		{
			scanf("%lld%lld",&q,&h);
			shu=0;
			chazhao(1);
			cout<<shu<<endl;
		}
	}
	return 0;
}

今天的线段树就先讲到这里，大家快去试试吧。