【POJ 1845】Sumdiv——数论质因数 + 分治 + 快速幂

（题面来自luogu）

题目描述

输入两个正整数a和b，求a^b的所有因子之和。结果太大，只要输出它对9901的余数。

输入格式

仅一行，为两个正整数a和b(0≤a,b≤50000000)。

输出格式

a^b的因子和对9901的余数。

　　题中给出的数据很大，暴力明显不可取。顺着题目的思路，我们需要表示出a^b的所有约数之和。考虑把a质因数分解，则原式可以表示为：

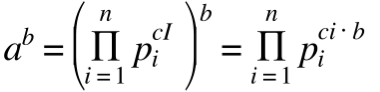
　　那么上式的所有因数就是它的质因数的组合相乘构成的集合。令它们求和，可以发现，和式可以因式分解后表示为

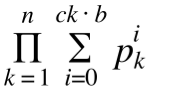
　　这个式子把所求的答案表示成了若干和式相乘的形式，可以较为方便的进行取模。而前9个质数之积已经超过了给定范围，原式的乘数不会很多，因此把每个和式的答案算出来暴力相乘即可。

　　观察发现每个和式都是等比数列求和的形式；如果直接套用公式，需要做除法，可以使用费马小定理求出每个除数的逆元来做。因为我觉得逆元很麻烦，这里依照算法进阶的思路，使用分治在log^2的复杂度内求出每个和式的结果。当ci * b为奇数时：

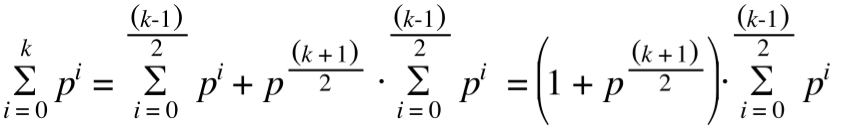
　　这个式子每进行一次分解，和式的项数就会缩小一半，很适合进行分治计算；式中提出的p的幂可以用快速幂来算出。当ci * b是偶数时，可以提出一个p来变为奇数处理。那么等比数列求和也可以在可承受的复杂度内解决了。

　　本题的总体思路：质因数分解a^b，把所求因数和因式分解为每个质因数的若干次幂等比求和相乘的形式后，分治递归求出每一个等比数列的和。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int mod(9901), msqrt(7100), maxn(50000000);
int A, B;
int prime[msqrt];
bool vis[msqrt];
void euler() { //欧拉筛
for (int i = 2; i <= msqrt; ++i) {
if (!vis[i])
prime[++prime[0]] = i;
for (int j = 1; j <= prime[0] && prime[j] * i <= msqrt; ++j) {
vis[prime[j] * i] = true;
if (i % prime[j] == 0)
break;
}
}
/* int t = 1;
for (int i = 1; i <= prime[0]; ++i) { //暴力确定质因数的最多个数
t *= prime[i];
if (t > maxn) {
cout << i << " " << t;
break;
}
}*/
}
int fc[20][2], top;
void Get_factors(int x, const int &B) { //质因数分解
for (int i = 1; i <= prime[0] && x; ++i)
if (x % prime[i] == 0) {
fc[++top][0] = prime[i];
while (x % prime[i] == 0)
++fc[top][1], x /= prime[i];
fc[top][1] *= B;
}
if (x > 1)//A is a big prime
fc[++top][0] = x, fc[top][1] = B;
}
int ans = 1;
int fpow(int a, int b) {
int ret = 1;
while (b) {
if (b & 1)
ret = ret * a % mod;
b >>= 1;
a = a * a % mod;
}
return ret;
}
int calc(int a, int b) { //计算各等比数列之和
if (b == 0) return 1;
if (b & 1)
return (1 + fpow(a, (b + 1) >> 1)) * calc(a, b >> 1) % mod;
return (1 + a * calc(a, b - 1)) % mod;
}
int main() {
cin >> A >> B;
if (A == 0) { //特判
putchar('0');
return 0;
}
euler();
Get_factors(A, B);
for (int i = 1; i <= top; ++i)
ans = (ans * calc(fc[i][0] % mod, fc[i][1])) % mod;
cout << ans;
return 0;
}