编译原理：DFA最小化，语法分析初步

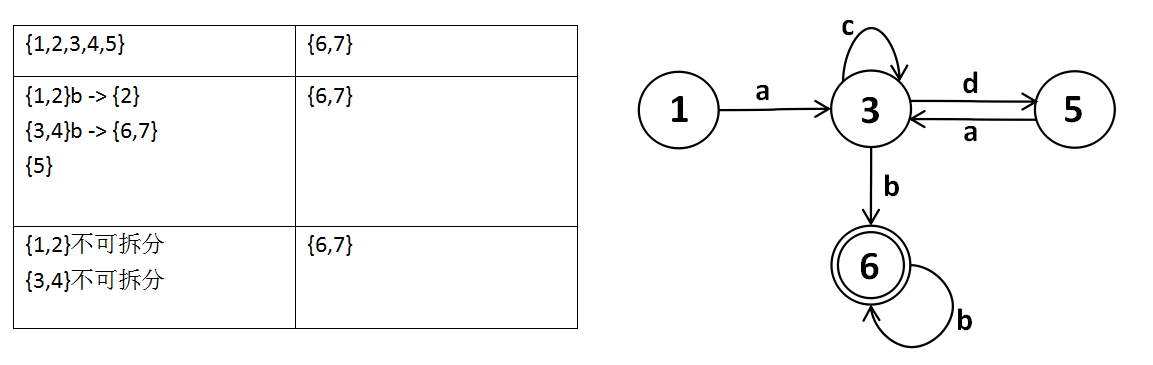
1.将DFA最小化：教材P65 第9题

　　　　 

解析：

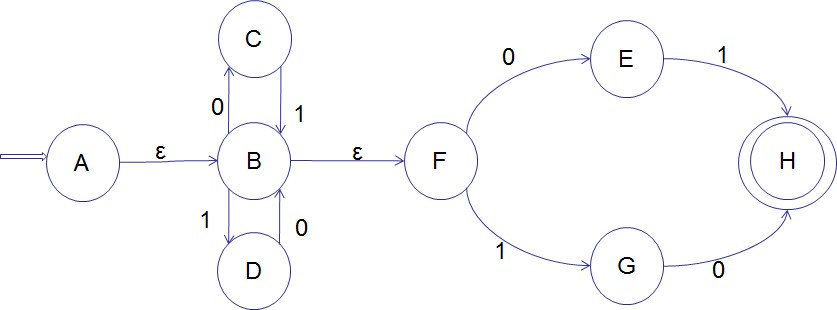
2.构造以下文法相应的最小的DFA

S→ 0A|1B

A→ 1S|1

B→0S|0

解析：

S→ 0A|1B

→S

→ 0(1S|1)|1(0S|0)

→01S | 01 | 10S | 10

→(01 | 10)S | (01 | 10)

→(01 | 10)*(01 | 10)

由正规式可得NFA如下：

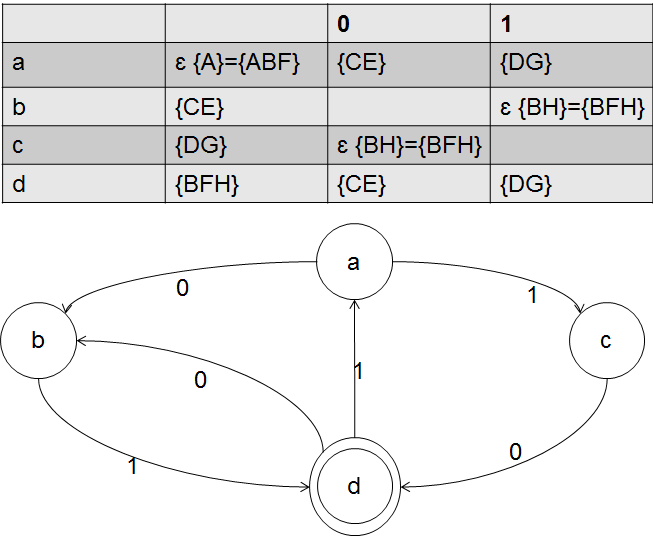
由NFA可得DFA状态转换矩阵以及图如下：

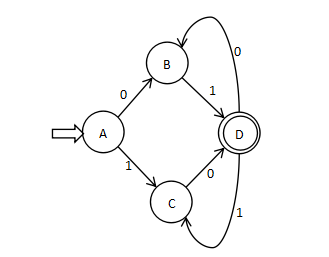
最小化DFA如下：

状态转换图如下：

3.给定如下文法 G[S]：

S →AB

A → aA | ɛ

B → b | bB

给出句子aaab 的一个自顶向下语法分析过程，并说明回溯产生的原因是什么？

解析：句子aaab 的一个自顶向下语法分析过程如下：

　　S=>AB

　　  =>aAB

　　  =>aaAB

　　  =>aaaAB

　　  =>aaaεB

　　  =>aaab

　　回溯产生的原因是文法的产生式有公共左因子。

4.P100 练习4，反复提取公共左因子，对文法进行改写。

解析：

S→C$

C→bA|aB

A→a|aC|bAA

B→b|bC|aBB

解：

提取公共左因子得

S->C$

C->bA|aB

A->aD|bAA

B->bE|aBB

D->ε|C