java 基础--8 种基本数据类型：整型、浮点型、布尔型、字符型 整型中 byte、short、int、long 的取值范围 什么是浮点型？什么是单精度和双精度？为什么不能用浮点型表示金额？

 一、8种基本数据类型(4整,2浮,1符,1布)：

整型：byte（最小的数据类型）、short（短整型）、int（整型）、long（长整型）；

浮点型：float（浮点型）、double（双精度浮点型）；

字符型：char（字符型）；

布尔型：boolean（布尔型）。

二、整型中 byte、short、int、long 取值范围

byte：一个字节有8位，去掉符号位还有7位，正数为避免进位还要减1，因此byte的取值范围为：-2^7 ～ (2^7-1)，也就是 -128～127 之间。

short：short用16位存储，去掉符号位还有15位，正数为避免进位还要减1，因此short的取值范围是：-2^15 ~ (2^15-1)。

int：整型用32位存储，去掉符号位还有31位，正数为避免进位还要减1，因此整型的取值范围是 -2^31 ~ (2^31-1)。

long：长整型用64位存储，去掉符号位还有63位，正数为避免进位还要减1，因此长整型的取值范围是 -2^63 ~ (2^63-1)。

三：浮点型数据

浮点类型是指用于表示小数的数据类型。

单精度和双精度的区别：

单精度浮点型float，用32位存储，1位为符号位, 指数8位, 尾数23位，即：float的精度是23位，能精确表达23位的数，超过就被截取。

双精度浮点型double，用64位存储，1位符号位,11位指数,52位尾数，即：double的精度是52位，能精确表达52位的数，超过就被截取。

双精度类型double比单精度类型float具有更高的精度，和更大的表示范围，常常用于科学计算等高精度场合。

浮点数与小数的区别：

1）在赋值或者存储中浮点类型的精度有限，float是23位，double是52位。

2）在计算机实际处理和运算过程中，浮点数本质上是以二进制形式存在的。

    3）二进制所能表示的两个相邻的浮点值之间存在一定的间隙，浮点值越大，这个间隙也会越大。如果此时对较大的浮点数进行操作时，浮点数的精度问题就会产生，甚至出现一些“不正常"的现象。

为什么不能用浮点数来表示金额

先给出结论：金额用BigDecimal ！！！

1）精度丢失问题

从上面我们可以知道，float的精度是23位，double精度是63位。在存储或运算过程中，当超出精度时，超出部分会被截掉，由此就会造成误差。

对于金额而言，舍去不能表示的部分，损失也就产生了。

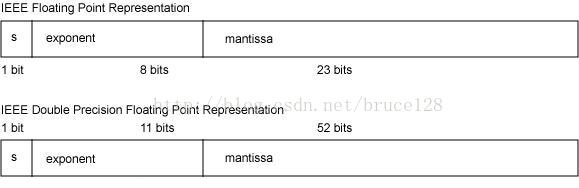
32位的浮点数由3部分组成：1比特的符号位，8比特的阶码（exponent,指数），23比特的尾数（Mantissa，尾数）。这个结构会表示成一个小数点左边为1，以底数为2的科学计数法表示的二进制小数。浮点数的能表示的数据大小范围由阶码决定，但是能够表示的精度完全取决于尾数的长度。long的最大值是2的64次方减1，需要63个二进制位表示，即便是double，52位的尾数也无法完整的表示long的最大值。不能表示的部分也就只能被舍去了。对于金额，舍去不能表示的部分，损失也就产生了。
  了解了浮点数表示机制后，丢失精度的现象也就不难理解了。但是，这只是浮点数不能表示金额的原因之一。还有一个深刻的原因与进制转换有关。十进制的0.1在二进制下将是一个无线循环小数。

eg：

public class MyTest {
    public static void main(String[] args) {
        float increment = 0.1f;
        float expected = 1;
        float sum = 0;
        for (int i = 0; i < 10; i++) {
            sum += increment;
            System.out.println(sum);
        }  

        if (expected == sum) {
            System.out.println("equal");
        } else {
            System.out.println("not equal ");
        }
    }
}  

输出结果：

0.1
0.2
0.3
0.4
0.5
0.6
0.70000005
0.8000001
0.9000001
1.0000001
not equal   

2）进制转换误差

从上面我们可以知道，在计算机实际处理和运算过程中，浮点数本质上是以二进制形式存在的。

而十进制的0.1在二进制下将是一个无限循环小数，这就会导致误差的出现。

如果一个小数不是2的负整数次幂，用浮点数表示必然产生浮点误差。

换言之：A进制下的有限小数，转换到B进制下极有可能是无限小数，误差也由此产生。

金额计算不能用doube!!!!

金额计算不能用doube!!!!

金额计算不能用doube!!!!
金额计算必须用BigDecimal

浮点数不精确的根本原因在于：尾数部分的位数是固定的，一旦需要表示的数字的精度高于浮点数的精度，那么必然产生误差！

解决这个问题的方法是BigDecimal的类，这个类可以表示任意精度的数字，其原理是：用字符串存储数字，转换为数组来模拟大数，实现两个数组的数学运算并将结果返回。

BigDecimal的使用要点：

    1、BigDecimal变量初始化——必须用传入String的构造方法

BigDecimal num1 = new BigDecimal(0.005);//用数值转换成大数，有误差
BigDecimal num12 = new BigDecimal("0.005");//用字符串转换成大数，无误差

　　    因为：不是所有的浮点数都能够被精确的表示成一个double 类型值，有些浮点数值不能够被精确的表示成 double 类型值时，它会被表示成与它最接近的 double 类型的值，此时用它来初始化一个大数，会“先造成了误差，再用产生了误差的值生成大数”，也就是“将错就错”。

    2、使用除法函数在divide的时候要设置各种参数，要精确的小数位数和舍入模式，其中有8种舍入模式：

 

1、ROUND_UP

远离零的舍入模式。

在丢弃非零部分之前始终增加数字(始终对非零舍弃部分前面的数字加1)。

注意，此舍入模式始终不会减少计算值的大小。

2、ROUND_DOWN

接近零的舍入模式。

在丢弃某部分之前始终不增加数字(从不对舍弃部分前面的数字加1，即截短)。

注意，此舍入模式始终不会增加计算值的大小。

3、ROUND_CEILING

接近正无穷大的舍入模式。

如果 BigDecimal 为正，则舍入行为与 ROUND_UP 相同;

如果为负，则舍入行为与 ROUND_DOWN 相同。

注意，此舍入模式始终不会减少计算值。

4、ROUND_FLOOR

接近负无穷大的舍入模式。

如果 BigDecimal 为正，则舍入行为与 ROUND_DOWN 相同;

如果为负，则舍入行为与 ROUND_UP 相同。

注意，此舍入模式始终不会增加计算值。

5、ROUND_HALF_UP

向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则为向上舍入的舍入模式。

如果舍弃部分 >= 0.5，则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同。

注意，这是我们大多数人在小学时就学过的舍入模式(四舍五入)。

6、ROUND_HALF_DOWN

向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则为上舍入的舍入模式。

如果舍弃部分 > 0.5，则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同(五舍六入)。

7、ROUND_HALF_EVEN

向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则向相邻的偶数舍入。

如果舍弃部分左边的数字为奇数，则舍入行为与 ROUND_HALF_UP 相同;

如果为偶数，则舍入行为与 ROUND_HALF_DOWN 相同。

注意，在重复进行一系列计算时，此舍入模式可以将累加错误减到最小。

此舍入模式也称为“银行家舍入法”，主要在美国使用。

如果前一位为奇数，则入位，否则舍去。

以下例子为保留小数点1位，那么这种舍入方式下的结果。

1.15>1.2 1.25>1.2

8、ROUND_UNNECESSARY

断言请求的操作具有精确的结果，因此不需要舍入。

如果对获得精确结果的操作指定此舍入模式，则抛出ArithmeticException。