<老古董>线性支持向量机中的硬间隔(hard margin)和软间隔(soft margin)是什么

_________________________________________________________________________________________________

The support-vector mechine is a new learning machine for two-group classification problems. The machine conceptually implements the following idea: input vectors are non-linearly mapped to a very high-dimension feature space. In this feature space a linear decision surface is constructed. Special properties of the decision surface ensures high generalization ability of the learning machine. The idea behind the support-vector network was previously implemented for the restricted case where the training data can be separated without errors. We here extend this result to non-separable training data.

High generalization ability of support-vector networks utilizing polynomial input transformations is demonstrated. We also compare the performance of the support-vector network to various classical learning algorithms that all took part in a benchmark study of Optical Character Recognition.

摘自eptember 1995, Volume 20, Issue 3, pp 273–297

_________________________________________________________________________________________________

支持向量机，上世纪流行的一种用来解决二分类问题的模型。

它可以这样理解————我们使用一组样本( ,y_i)（其中y∈{-1,1}，称为标签；为一维向量，称为特征）来构建模型(训练模型)。咋说呢，借助坐标系把这些点的特征在空间中表示出来，使用两种颜色来表示y。需要寻找一个平面把这些点划分为两类。这个平面就是我们的分类器。表示出来一看呢，有的是线性可分的，有的是线性不可分的。分别如下面二图。

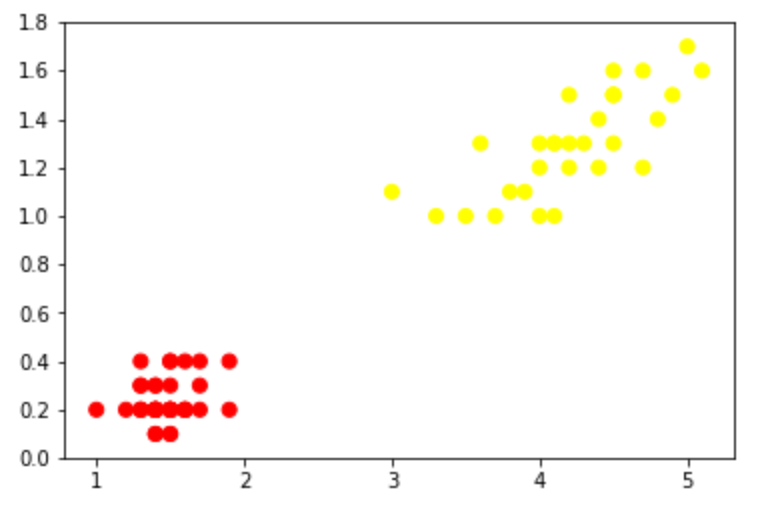
SVM刚诞生时遇到的问题大多都如前者，这样我们直接计算“最大间隔超平面”就ok，这个称为“线性支持向量机”，即最初的SVM；（作者————1963年，万普尼克）

后来，遇到了更多复杂的情况(如第二张图)，大家希望能改进SVM，使它也能够很好地处理后者，于是把核技巧拿到了SVM上，借助核函数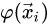将原特征向量映射到高维空间，使它可以一刀划分开来(像上面的左图)，再计算“最大间隔超平面”。经过这一改进之后，SVM的泛化能力大大加强。这个称为“非线性支持向量机”。（作者————1992年，Bernhard E. Boser、Isabelle M. Guyon和弗拉基米尔·万普尼克）

_________________________________________________________________________________________________

1962年出生的线性支持向量机中有两个概念：“硬间隔”，“软间隔”。

“硬间隔”“软间隔”是概念，而不是性质。像训练数据的“线性可分”“线性不可分”就是一种性质。

如果我们的训练数据集是线性可分的，那么可以找到一个超平面将训练数据集严格地划开，分为两类(可以想象成一个平板)。我们找两个这样的超平面，它们满足1.两者平行2.两者距离最大（即下图中的两条虚线）。两个超平面上的样本x们称为”支持向量“。“最大间隔超平面”(也就是分类器)是两超平面的平均值。我们定义这两个超平面间的区域为“间隔”。在这种情况下它就是“硬间隔”。

最大间隔超平面可以表示为：  W*X+b = 0

两个超平面可以分别表示为：  W*X+b = 1，W*X+b = -1

对于数据线性不可分的情况(上图)，我们引入铰链损失函数，

当约束条件 (1) 满足时（也就是如果  位于边距的正确一侧）此函数为零。对于间隔的错误一侧的数据，该函数的值与距间隔的距离成正比。 然后我们希望最小化(参数 用来权衡增加间隔大小与确保  位于间隔的正确一侧之间的关系)

这时的“间隔”就是“软间隔”。

总结一下，我们构建模型使用的数据集如果是严格可一刀分开的， 那么两超平面间的间隔就是“硬间隔”；如果不是严格可以一刀分开的，两超平面间的间隔就是“软间隔”。这是针对线性支持向量机而言。哈哈哈有人说了线性支持向量机都五十年前的东西了，还不如说说非线性支持向量机。进入非线性支持向量机时代后，“硬间隔”“软间隔”是对于核函数变换后的超平面而言的了。

现在对付“软间隔”我们都用“泛化”和“拟合”了，上世纪机器学习刚起步的时候可没这么多东西。可以说是冷兵器时代，如今科技发达，处理二分类问题我们可以用很多技术——逻辑回归啊，神经网络啊，各种聚类算法啊，等等。

参考：

1.  https://link.springer.com/article/10.1007%2FBF00994018

2.  https://en.wikipedia.org/wiki/Support-vector_machine