PCA(主成分分析)方法浅析

降维、数据压缩

找到数据中最重要的方向：方差最大的方向，也就是样本间差距最显著的方向

在与第一个正交的超平面上找最合适的第二个方向

PCA算法流程

上图第一步描述不正确，应该是去中心化，而不是中心化

具体来说，投影这一环节就是：将与特征值对应的k个特征向量分别作为行向量组成特征向量矩阵P

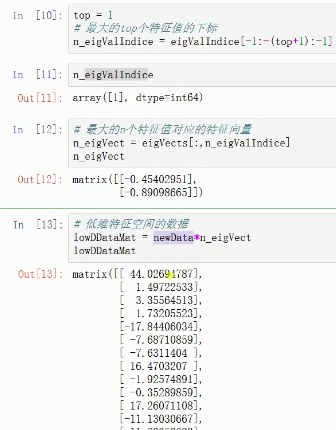
直接乘以特征变量就好。原来是二维数据，降维之后只有一维。

我们想保留几个维度的特征，就留下几个特征值和对应的特征向量。

PCA(主成分分析)方法浅析的更多相关文章

  1. PCA主成分分析方法

    PCA: Principal Components Analysis,主成分分析. 1.引入 在对任何训练集进行分类和回归处理之前,我们首先都需要提取原始数据的特征,然后将提取出的特征数据输入到相应的 ...

  2. 核主成分分析方法（KPCA）怎么理解？

    先回顾下主成分分析方法.PCA的最大方差推导的结论是,把数据投影到特征向量的方向后,方差具有极大值的.假如先把数据映射到一个新的特征空间,再做PCA会怎样?对于一些数据,方差会更好地保留下来.而核方法 ...

  3. 机器学习之PCA主成分分析

    前言            以下内容是个人学习之后的感悟,转载请注明出处~ 简介 在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性.人们自然希望变量个数较少而得到的 信息较多.在很 ...

  4. PCA主成分分析Python实现

    作者:拾毅者 出处:http://blog.csdn.net/Dream_angel_Z/article/details/50760130 Github源代码:https://github.com/c ...

  5. 数据降维-PCA主成分分析

    1.什么是PCA? PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法.PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特 ...

  6. 机器学习 - 算法 - PCA 主成分分析

    PCA 主成分分析 原理概述 用途 - 降维中最常用的手段 目标 - 提取最有价值的信息( 基于方差 ) 问题 - 降维后的数据的意义 ? 所需数学基础概念 向量的表示 基变换 协方差矩阵 协方差 优 ...

  7. PCA主成分分析（上）

    PCA主成分分析 PCA目的 最大可分性(最大投影方差) 投影 优化目标 关键点 推导 为什么要找最大特征值对应的特征向量呢? 之前看3DMM的论文的看到其用了PCA的方法,一开始以为自己对于PCA已 ...

  8. C# Winform窗口之间传值的多种方法浅析（转）

    摘要http://www.jb51.net/article/63837.htm 这篇文章主要介绍了C# Winform窗口之间传值的多种方法浅析,本文起讲解了通过构造器传值.通过属性传递.通过事件携带 ...

  9. 用PCA(主成分分析法)进行信号滤波

    用PCA(主成分分析法)进行信号滤波 此文章从我之前的C博客上导入,代码什么的可以参考matlab官方帮助文档 现在网上大多是通过PCA对数据进行降维,其实PCA还有一个用处就是可以进行信号滤波.网上 ...

随机推荐

  1. （main）贝叶斯统计 | 贝叶斯定理 | 贝叶斯推断 | 贝叶斯线性回归 | Bayes' Theorem

    2019年08月31日更新 看了一篇发在NM上的文章才又明白了贝叶斯方法的重要性和普适性,结合目前最火的DL,会有意想不到的结果. 目前一些最直觉性的理解: 概率的核心就是可能性空间一定,三体世界不会 ...

  2. 彻底搞清楚javascript中的require、import和export(js模块加载规范的前世今生)

    为什么有模块概念 理想情况下,开发者只需要实现核心的业务逻辑,其他都可以加载别人已经写好的模块. 但是,Javascript不是一种模块化编程语言,在es6以前,它是不支持”类”(class),所以也 ...

  3. cls只能调用一次实例 第二次None

    class Zarten(): _singleton = None def __new__(cls, *args, **kwargs): print('__new__') if not cls._si ...

  4. Build Telemetry for Distributed Services之Open Telemetry简介

    官网链接:https://opentelemetry.io/about/ OpenTelemetry is the next major version of the OpenTracing and  ...

  5. RAID概念记录

    之前对RAID概念有一些基本的认知,这次同事培训k8s 的持久卷,提到了RAID的一些概念和用法,记录一下. RAID ( Redundant Array of Independent Disks ) ...

  6. 使用apache commons net进行ftp传输

    apache commons net的maven地址: http://mvnrepository.com/artifact/commons-net/commons-net/3.6 <!-- ht ...

  7. 在谷歌中缓存下载视频离线观看,js代码

    var download=function(urlInfo) { when(createFile(localFileName)) .then(function (fileInfo) { var dow ...

  8. Flutter之切换导航TabBar组件

    TabController 这是Tab页的控制器,用于定义Tab标签和内容页的坐标,还可配置标签页的切换动画效果等. TabController的创建有两种形式,一种是使用系统的DefaultTabC ...

  9. 纯css实现表单输入验证

    <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...

  10. 3rd.botan

    1.HOME 1.官网:https://botan.randombit.net/ Win下 编译步骤:https://botan.randombit.net/handbook/building.htm ...