LeetCode 双周赛 102，模拟 / BFS / Dijkstra / Floyd

本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 提问。

大家好，欢迎来到小彭的 LeetCode 周赛解题报告。

昨晚是 LeetCode 双周赛第 102 场，你参加了吗？这场比赛比较简单，拼的是板子手速，继上周掉大分后算是回了一口血。

2618. 查询网格图中每一列的宽度（Easy）

简单模拟题，无需解释。

模拟：$O(nm)$

2619. 一个数组所有前缀的分数（Medium）

简单动态规划题，简单到像模拟题。

动态规划：$O(n)$

2620. 二叉树的堂兄弟节点 II（Medium）

思考过程：递归→DFS→BFS。由于堂兄弟节点都在同一层，发现 “递归地减少问题规模求解原问题” 和 DFS 都不好编码，而 BFS 更符合 “层” 的概念。往 BFS 方向思考后，容易找到解决方法。

BFS：$O(n)$

2621. 设计可以求最短路径的图类（Hard）

最近周赛的最短路问题非常多，印象中已经连续出现三次最短路问题。理解 Dijkstra 算法和 Floyd 算法的应用场景非常重要。

朴素 Dijkstra：$O(m + q_1·n^2 + q_2)$
Dijkstra + 最小堆：$O(m + q_1·nlgm+q_2)$
Floyd：$O(m + n^3 + q_1 + q_2·n^2)$

2618. 查询网格图中每一列的宽度（Easy）

题目地址

https://leetcode.cn/problems/find-the-width-of-columns-of-a-grid/description/

题目描述

给你一个下标从 0 开始的 m x n 整数矩阵 grid 。矩阵中某一列的宽度是这一列数字的最大 字符串长度 。

比方说，如果 grid = [[-10], [3], [12]] ，那么唯一一列的宽度是 3 ，因为 10 的字符串长度为 3 。

请你返回一个大小为 n 的整数数组 ans ，其中 ans[i] 是第 i 列的宽度。

一个有 len 个数位的整数 x ，如果是非负数，那么 字符串长度 为 len ，否则为 len + 1 。

题解（模拟）

class Solution {

    fun findColumnWidth(grid: Array<IntArray>): IntArray {

        val m = grid.size

        val n = grid[0].size

        val ret = IntArray(n)

        for (column in 0 until n) {

            for (row in 0 until m) {

                ret[column] = Math.max(ret[column], "${grid[row][column]}".length)

            }

        }

        return ret

    }

}

复杂度分析：

时间复杂度：$O(nm)$ 其中 $n$ 和 $m$ 为 grid 数组的行列大小，每个节点最多访问 1 次；
空间复杂度：$O(1)$ 不考虑结果数组。

2619. 一个数组所有前缀的分数（Medium）

题目地址

https://leetcode.cn/problems/find-the-score-of-all-prefixes-of-an-array/description/

题目描述

定义一个数组 arr 的 转换数组 conver 为：

conver[i] = arr[i] + max(arr[0..i])，其中 max(arr[0..i]) 是满足 0 <= j <= i 的所有 arr[j] 中的最大值。

定义一个数组 arr 的分数为 arr 转换数组中所有元素的和。

给你一个下标从 0 开始长度为 n 的整数数组 nums ，请你返回一个长度为 n 的数组 **ans ，其中 ans[i]是前缀 nums[0..i] 的分数。

题解（动态规划）

简单动态规划题，容易发现递归关系：

conver[i] = max
dp[i] = dp[i-1] + conver[i]

class Solution {

    fun findPrefixScore(nums: IntArray): LongArray {

        val n = nums.size

        val ret = LongArray(n)

        // 初始状态

        ret[0] = 2L * nums[0]

        var maxNum = nums[0]

        // DP

        for (i in 1 until n) {

            maxNum = Math.max(maxNum, nums[i])

            ret[i] = ret[i - 1] + (0L + nums[i] + maxNum)

        }

        return ret

    }

}

复杂度分析：

时间复杂度：$O(n)$ 其中 $n$ 为 $arr$ 数组的长度，每个节点最多访问 1 次；
空间复杂度：$O(1)$ 不考虑结果数组。

2620. 二叉树的堂兄弟节点 II（Medium）

题目地址

https://leetcode.cn/problems/cousins-in-binary-tree-ii/description/

题目描述

给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。

请你返回修改值之后，树的根 **root **。

注意，一个节点的深度指的是从树根节点到这个节点经过的边数。

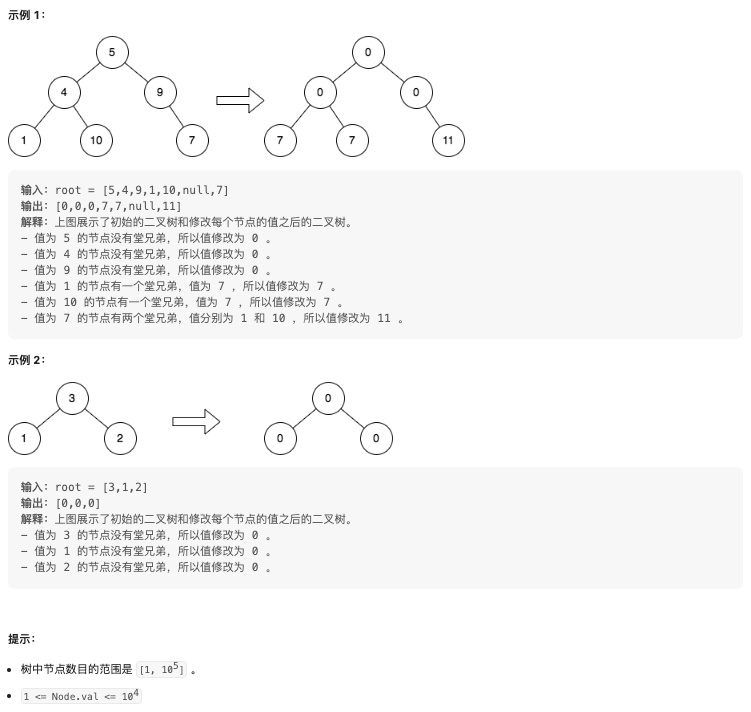
题解（BFS）

分析 1 - 递归：尝试分解左右子树求解问题，发现左右子树不独立，不再考虑此思路；

分析 2 - DFS / BFS：由于堂兄弟节点都在同一层，而 BFS 更符合 “层” 的概念，往 BFS 方向思考后，容易找到解决方法：在处理每一层的节点时，第一轮遍历先累计下一层节点的和，在第二轮遍历时更新下一层节点（取出自己和兄弟节点的值）。

/**

 * Example:

 * var ti = TreeNode(5)

 * var v = ti.`val`

 * Definition for a binary tree node.

 * class TreeNode(var `val`: Int) {

 *     var left: TreeNode? = null

 *     var right: TreeNode? = null

 * }

 */

class Solution {

    fun replaceValueInTree(root: TreeNode?): TreeNode? {

        if (null == root) return root

        // BFS

        val queue = LinkedList<TreeNode>()

        queue.offer(root)

        root.`val` = 0

        while (!queue.isEmpty()) {

            val size = queue.size

            // 计算下一层的和

            var nextLevelSum = 0

            for (i in 0 until size) {

                val node = queue[i]

                if (null != node.left) nextLevelSum += node.left.`val`

                if (null != node.right) nextLevelSum += node.right.`val`

            }

            for (count in 0 until size) {

                val node = queue.poll()

                // 减去非堂兄弟节点

                var nextLevelSumWithoutNode = nextLevelSum

                if (null != node.left) nextLevelSumWithoutNode -= node.left.`val`

                if (null != node.right) nextLevelSumWithoutNode -= node.right.`val`

                // 入队

                if (null != node.left) {

                    queue.offer(node.left)

                    node.left.`val` = nextLevelSumWithoutNode

                }

                if (null != node.right) {

                    queue.offer(node.right)

                    node.right.`val` = nextLevelSumWithoutNode

                }

            }

        }

        return root

    }

}

复杂度分析：

时间复杂度：$O(n)$ 其中 n 为二叉树的节点总数，每个节点最多访问 2 次（含入队 1 次）；
空间复杂度：$O(n)$ BFS 队列空间。

相似题目：

993. 二叉树的堂兄弟节点

2621. 设计可以求最短路径的图类（Hard）

题目地址

https://leetcode.cn/problems/design-graph-with-shortest-path-calculator/

题目描述

给你一个有 n 个节点的 有向带权 图，节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示，其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。

请你实现一个 Graph 类：

Graph(int n, int[][] edges) 初始化图有 n 个节点，并输入初始边。
addEdge(int[] edge) 向边集中添加一条边，其中 ****edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径最小代价。如果路径不存在，返回 1 。一条路径的代价是路径中所有边代价之和。

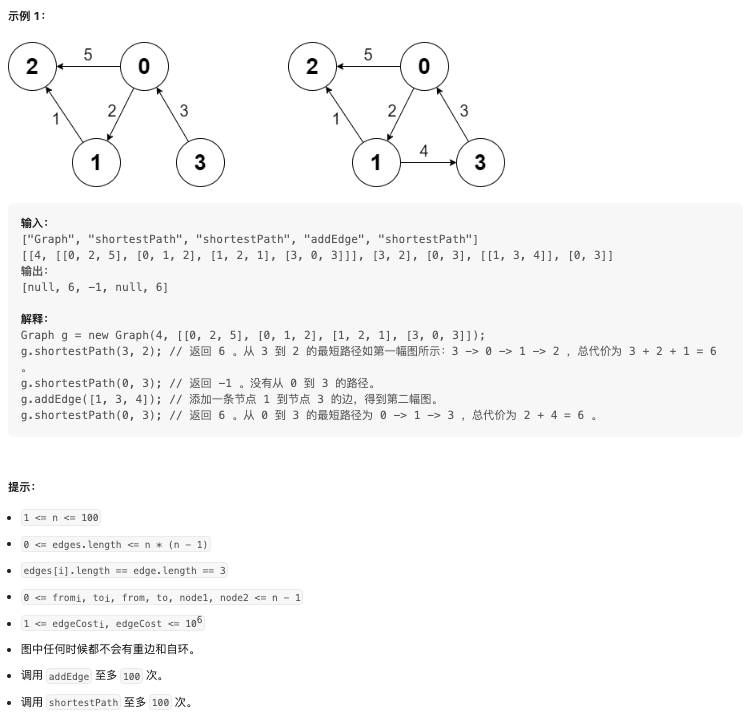
问题分析

这道题勉强能算 Floyd 算法或 Dijkstra 算法的模板题，先回顾一下最短路问题解决方案：

Dijkstra 算法（单源正权最短路）：
- 本质上是贪心 + BFS；
- 负权边会破坏贪心策略的选择，无法处理含负权问题；
- 稀疏图小顶堆的写法更优，稠密图朴素写法更优。
Floyd 算法（多源汇正权最短路）
Bellman Ford 算法（单源负权最短路）
SPFA 算法（单源负权最短路）

由于这道题需要支持多次查询操作，而 Floyd 算法能够缓存最短路结果，理论上 Floyd 算法是更优的选择。不过，我们观察到题目的数据量非常非常小，所以朴素 Dijkstra 算法也能通过。

题解一（朴素 Dijkstra）

这道题的查询操作是求从一个源点到目标点的最短路径，并且这条路径上没有负权值，符合 Dijkstra 算法的应用场景，在处理添加边时，只需要动态的修改图数据结构。

Dijkstra 算法的本质是贪心 + BFS，我们需要将所有节点分为 2 类，在每一轮迭代中，我们从 “候选集” 中选择距离起点最短路长度最小的节点，由于该点不存在更优解，所以可以用该点来 “松弛” 相邻节点。

1、确定集：已确定（从起点开始）到当前节点最短路径的节点；
2、候选集：未确定（从起点开始）到当前节点最短路径的节点。

技巧：使用较大的整数 0x3F3F3F3F 代替整数最大值 Integer.MAX_VALUE 可以减少加法越界判断。

class Graph(val n: Int, edges: Array<IntArray>) {

    private val INF = 0x3F3F3F3F

    // 带权有向图（临接矩阵）

    private val graph = Array(n) { IntArray(n) { INF } }

    init {

        // i 自旋的路径长度

        for (i in 0 until n) {

            graph[i][i] = 0

        }

        // i 直达 j 的路径长度

        for (edge in edges) {

            addEdge(edge)

        }

    }

    fun addEdge(edge: IntArray) {

        graph[edge[0]][edge[1]] = edge[2]

    }

    fun shortestPath(node1: Int, node2: Int): Int {

        // Dijkstra

        // 最短路

        val dst = IntArray(n) { INF }

        dst[node1] = 0

        // 确定标记

        val visited = BooleanArray(n)

        // 迭代 n - 1 次

        for (count in 0 until n - 1) {

            // 寻找候选集中最短路长度最短的节点

            var x = -1

            for (i in 0 until n) {

                if (!visited[i] && (-1 == x || dst[i] < dst[x])) x = i

            }

            // start 可达的节点都访问过 || 已确定 node1 -> node2 的最短路

            if (-1 == x || dst[x] == INF || x == node2) break

            visited[x] = true

            // 松弛相邻节点

            for (y in 0 until n) {

                dst[y] = Math.min(dst[y], dst[x] + graph[x][y])

            }

        }

        return if (INF == dst[node2]) -1 else dst[node2]

    }

}

复杂度分析：

时间复杂度：$O(m + q_1·n^2 + q_2)$ 其中 n 为节点数量，m 为边数量，$q_1$ 为查询次数，$q_2$ 为添加边次数。建图时间 O(m)，每个节点访问 n 次；
空间复杂度：$O(n^2 + n)$ 图空间 + 最短路数组

题解二（Dijkstra + 最小堆）

这道题是稠密图，朴素 Dijkstra 由于 Dijkstra + 最小堆。

朴素 Dijkstra 的每轮迭代中需要遍历 n 个节点寻找候选集中的最短路长度。事实上，这 n 个节点中有部分是 ”确定集“，有部分是远离起点的边缘节点，每一轮都遍历显得没有必要。我们使用小顶堆记录候选集中最近深度的节点。

class Graph(val n: Int, edges: Array<IntArray>) {

    private val INF = 0x3F3F3F3F

    // 带权有向图（临接矩阵）

    private val graph = Array(n) { IntArray(n) { INF } }

    init {

        // i 自旋的路径长度

        for (i in 0 until n) {

            graph[i][i] = 0

        }

        // i 直达 j 的路径长度

        for (edge in edges) {

            addEdge(edge)

        }

    }

    fun addEdge(edge: IntArray) {

        graph[edge[0]][edge[1]] = edge[2]

    }

    fun shortestPath(node1: Int, node2: Int): Int {

        // Dijkstra + 最小堆

        // 最短路

        val dst = IntArray(n) { INF }

        dst[node1] = 0

        val heap = PriorityQueue<Int>() { i1, i2 ->

            dst[i1] - dst[i2]

        }

        heap.offer(node1)

        while (!heap.isEmpty()) {

            // 使用 O(lgm) 时间找出最短路长度

            var x = heap.poll()

            // 松弛相邻节点

            for (y in 0 until n) {

                if (dst[x] + graph[x][y] < dst[y]) {

                    dst[y] = dst[x] + graph[x][y]

                    heap.offer(y)

                }

            }

        }

        return if (INF == dst[node2]) -1 else dst[node2]

    }

}

复杂度分析：

时间复杂度：$O(m + q_1·nlgm+q_2)$ 其中 n 为节点数量，m 为边数量，$q_1$ 为查询次数，$q_2$ 为添加边次数。建图时间 $O(m)$，每条边都会访问一次，每轮迭代取堆顶 O(lgm)。这道题边数大于点数，朴素写法更优。
空间复杂度：$O(n^2 + n)$ 图空间 + 堆空间。

题解三（Floyd）

Fload 算法的本质是贪心 + BFS，我们需要三层循环枚举中转点 i、枚举起点 j 和枚举终点 k，如果 dst[i][k] + dst[k][j] < dst[i][j]，则可以松弛 dst[i][j]。

这道题的另一个关键点在于支持调用 addEdge() 动态添加边，所以使用 Floyd 算法时要考虑如何更新存量图。

class Graph(val n: Int, edges: Array<IntArray>) {

    val INF = 0x3F3F3F3F

    // 路径长度（带权有向图）

    val graph = Array(n) { IntArray(n) { INF } }

    init {

        // i 自旋的路径长度

        for (i in 0 until n) {

            graph[i][i] = 0

        }

        // i 直达 j 的路径长度

        for (edge in edges) {

            graph[edge[0]][edge[1]] = edge[2]

        }

        // Floyd 算法

        // 枚举中转点

        for (k in 0 until n) {

            // 枚举起点

            for (i in 0 until n) {

                // 枚举终点

                for (j in 0 until n) {

                    // 比较 <i to j> 与 <i to p> + <p to j>

                    graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j])

                }

            }

        }

    }

    fun addEdge(edge: IntArray) {

        val (x, y, cost) = edge

        // 直达

        graph[x][y] = Math.min(graph[x][y], cost)

        // 枚举中转点

        for (k in intArrayOf(x, y)) {

            // 枚举起点

            for (i in 0 until n) {

                // 枚举终点

                for (j in 0 until n) {

                    // 比较 <i to j> 与 <i to k> + <k to j>

                    graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j])

                }

            }

        }

    }

    fun shortestPath(node1: Int, node2: Int): Int {

        return if (graph[node1][node2] == INF) -1 else graph[node1][node2]

    }

}

复杂度分析：

时间复杂度：$O(m + n^3 + q_1 + q_2·n^2)$ 其中 $n$ 为节点数量，$m$ 为边数量，$q_1$ 为查询次数，$q_2$ 为添加边次数。建图时间 $O(m + n^3)$，单次查询时间 $O(1)$，单次添加边时间 $O(n^2)$；
空间复杂度：$O(n^2)$ 图空间。

相关题目：

743. 网络延迟时间

近期周赛最短路问题：