【leetcode】42. 接雨水

目录

• 题目
• 题解

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

来源：力扣（LeetCode）

链接：https://leetcode.cn/problems/trapping-rain-water

题解

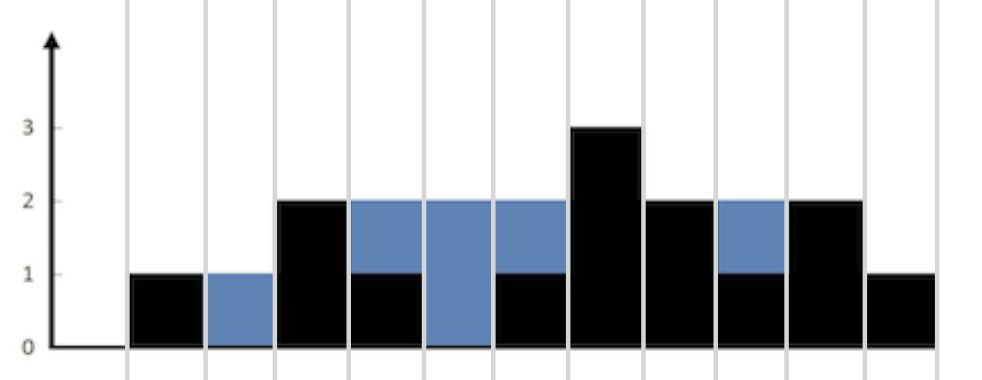
首先明确一个计算容积的方向——按照列来计算每个位置的容积，然后我们将每列的容积相加就得到整体的容积。将“示例1”中的容器按列划分，得到如上的图。

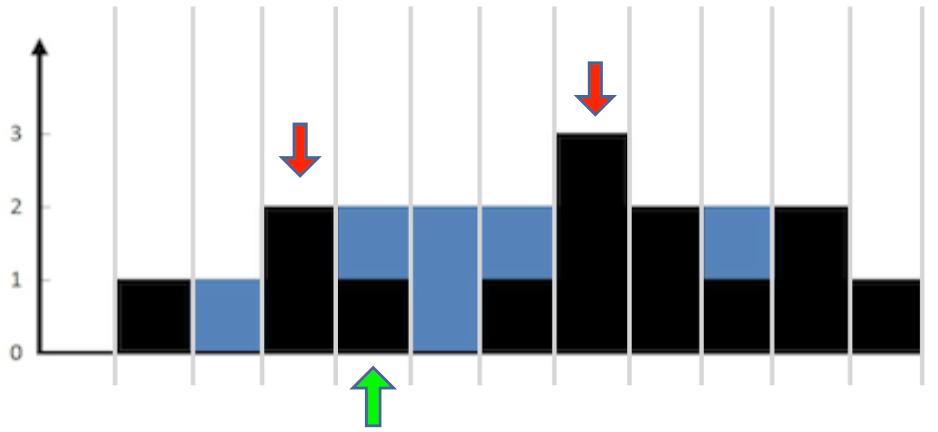
如何计算每个位置的容积呢？通过观察我们可以得出公式：位置i接水的容积 = Math.min([0,i)的最高位置, (i,length-1]的最高位置) - 位置i的高度。如下图所示：

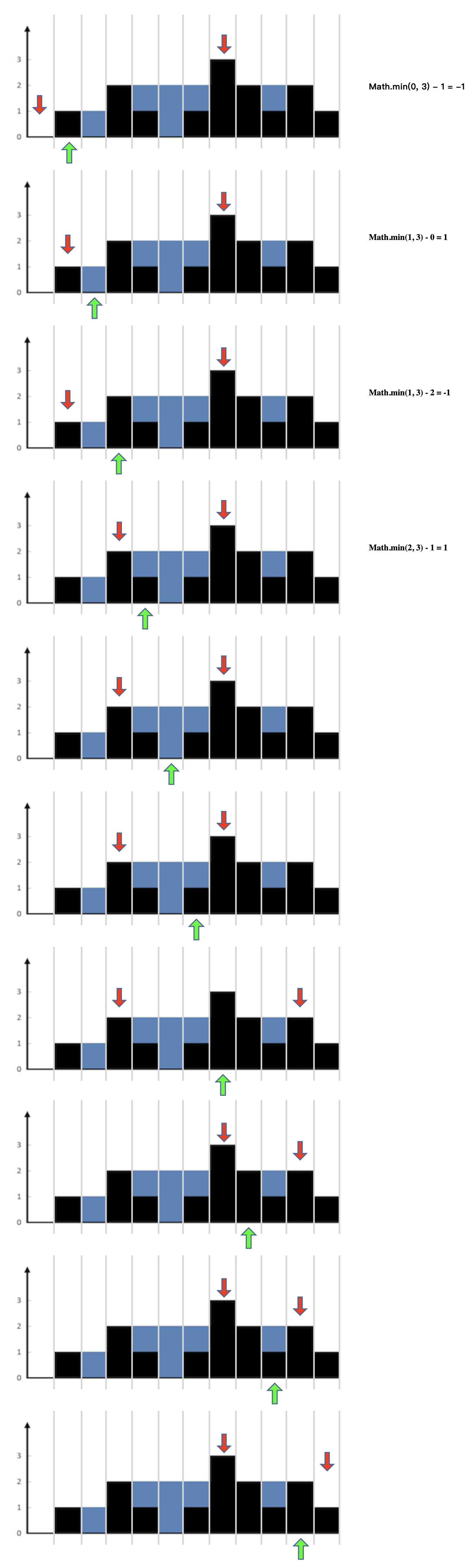
示例1的接水容积计算过程如下图所示：

所以，我们可以维护两个数组：

• 第一个数组left[i]中存储的是[0,i]的最大值
• 第二个数组right[i]中存储的是[i,length -1]的最大值

然后再遍历一遍数组，使用公式：位置i接水的容积 = Math.min(left[i-1], right[i+1]) - 位置i的高度就能得到位置i的接水容积，最后将每个位置的接水容积相加就能得到总的容积。

代码如下：

class Solution {
    public int trap(int[] height) {
        // left[i]记录的是0～i位置上的最大值
        int[] left = new int[height.length];
        // right[i]记录的是i～0位置上的最大值
        int[] right = new int[height.length];

        // 1.初始化left[]
        int leftMax = 0;
        for (int i = 0; i < height.length; i++) {
            leftMax = Math.max(leftMax, height[i]);
            left[i] = leftMax;
        }

        // 2.初始化right[]
        int rightMax = 0;
        for (int i = height.length - 1; i >= 0; i--) {
            rightMax = Math.max(rightMax, height[i]);
            right[i] = rightMax;
        }

        // 3.计算容积
        int result = 0;
        for (int i = 1; i < height.length - 1; i++) {
            int v = Math.min(left[i - 1], right[i + 1]) - height[i];

            if (v > 0) {
                result += v;
            }
        }

        return result;
    }
}