LeetCode 593. 有效的正方形（向量做法）

题目

题目链接：593. 有效的正方形

题意：给出二维平面上四个点的坐标，判断这四个点是否能构成一个正方形，四个点的输入顺序不做任何保证。

思路

通过向量运算可以很轻松地解决这道题。任取一点向其他三点连线，可以得到三个向量。我们将这三个向量按照其长度从小到大排序，分别称为 \(\boldsymbol{v}_0, \boldsymbol{v}_1, \boldsymbol{v}_2\)，若满足以下三个条件，则 \(\boldsymbol{v}_0, \boldsymbol{v}_1, \boldsymbol{v}_2\) 可以“张出”一个正方形（见下图）：

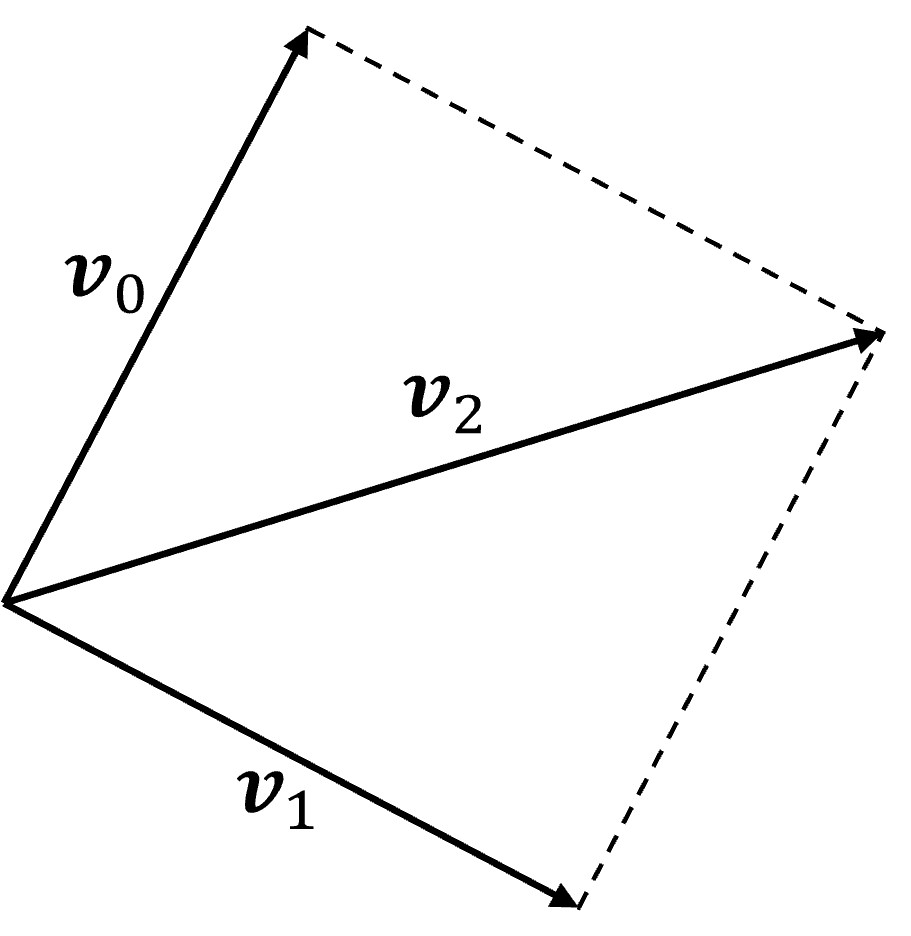
1. \(\boldsymbol{v}_0 + \boldsymbol{v}_1 = \boldsymbol{v}_2\)（四点构成平行四边形）
2. \(\Vert\boldsymbol{v}_0\Vert = \Vert\boldsymbol{v}_1\Vert\)（平行四边形 + 邻边相等，此时四点构成菱形）
3. \(\boldsymbol{v}_0 \cdot \boldsymbol{v}_1 = 0\)（菱形 + 直角，此时四点构成正方形）

我们还需要特别注意排除点重合的情况，例如四个点全部重合在一起，此时上面的三个条件仍然满足，但是不能构成正方形。

代码

以下为 Rust 语言的题解代码。

首先我们需要定义一个二维向量类型：

/// 二维向量
#[derive(Copy, Clone, Eq, PartialEq)]
struct Vector {
    x: i32,
    y: i32
}

impl Vector {
    fn new(from: (i32, i32), to: (i32, i32)) -> Self { Vector { x: to.0 - from.0, y: to.1 - from.1 } }
    /// 向量的模的平方
    fn len2(&self) -> i32 { self.x * self.x + self.y * self.y }
}

impl std::ops::Mul for Vector {
    type Output = i32;
    /// 向量点乘
    fn mul(self, rhs: Self) -> Self::Output { self.x * rhs.x + self.y * rhs.y }
}

impl std::ops::Add for Vector {
    type Output = Vector;
    /// 向量加法
    fn add(self, rhs: Self) -> Self::Output { Vector { x: self.x + rhs.x, y: self.y + rhs.y } }
}

解题函数如下：

impl Solution {
    pub fn valid_square(p1: Vec<i32>, p2: Vec<i32>, p3: Vec<i32>, p4: Vec<i32>) -> bool {
        let mut v = [
            Vector::new((p1[0], p1[1]), (p2[0], p2[1])),
            Vector::new((p1[0], p1[1]), (p3[0], p3[1])),
            Vector::new((p1[0], p1[1]), (p4[0], p4[1]))
        ];
        v.sort_by_key(Vector::len2);
        return v[0].len2() > 0            // 点不重合
            && v[0] + v[1] == v[2]        // 构成平行四边形
            && v[0].len2() == v[1].len2() // 构成菱形
            && v[0] * v[1] == 0;          // 构成正方形
    }
}

这种使用向量运算的解法有两个好处：

• 只需要对向量做一次排序即可解决顶点不按顺序的问题，不需要分类讨论，较为简洁。
• 全程都是整数运算，不需要担心浮点运算带来的舍入误差。

本题还有其他做法：

• 检查四边形的两条斜边
• 对顶点做旋转变换