最近公共祖先LCA Tarjan 离线算法

【简介】

解决LCA问题的Tarjan算法利用并查集在一次DFS（深度优先遍历）中完成所有询问。换句话说，要所有询问都读入后才开始计算，所以是一种离线的算法。

【原理】

先来看这样一个性质：当两个节点（u，v）的最近公共祖先是x时，那么我们可以确定的说，当进行后序遍历的时候，必然先访问完x的所有子树，其中包含u、v，然后才会返回到x所在的节点。这个性质就是我们使用Tarjan算法解决最近公共祖先问题的核心思想。

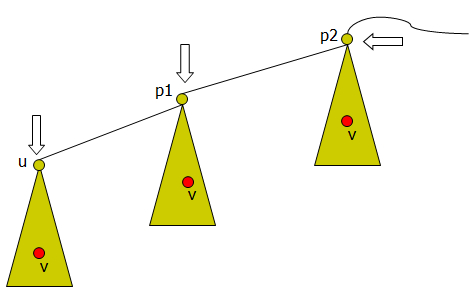
如上图所示，找出根节点到u得关键路径P ，已遍历的点位于路径P中某个点的子树中，当遍历到u时v已遍历过（u的子树已遍历完），那么v必然存在于子树p_k中，此时LCA(u,v)就等于现在v所在集合的祖先p_k。如果还没有遍历到，则继续遍历，只不过LCA(u,v)要等到遍历到v时才能知道了，原理如上。需要注意的一点是，为了保持上图的性质，如果一个节点的一个子树遍历完了，需要合并该节点的子树集合。

tarjan算法的步骤是(当dfs到节点u时):

（一） 在并查集中建立仅有u的集合,设置该集合的祖先为u
      （二） 对u的每个孩子v:
                  1. tarjan之
                  2. 合并v到父节点u的集合,确保集合的祖先是u
      （三）设置u为已遍历
      （四）处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)=  v所在的集合的祖先

【举例】

假设遍历完10的孩子,要处理关于10的请求了 取根节点到当前正在遍历的节点的路径为关键路径,即1-3-8-10 集合的祖先便是关键路径上距离集合最近的点 比如此时:     【1,2,5,6】为一个集合,祖先为1,集合中点和10的LCA为1     【3,7】为一个集合,祖先为3,集合中点和10的LCA为3     【8,9,11】为一个集合,祖先为8,集合中点和10的LCA为8     【10,12】为一个集合,祖先为10,集合中点和10的LCA为10 可以发现集合的祖先便是LCA ！

【HDU 2586】

换成Tarjan 离线算法来做。

 #pragma comment(linker, "/STACK:1024000000,1024000000")
 #include <stdio.h>
 #include <string.h>
 #include <vector>
 #include <cmath>
 using namespace std;
 int n,m;
 struct edge
 {
     int d,v,next;
     edge(){}
     edge(int _d,int _v,int _next)
     {
         d=_d;v=_v;next=_next;
     }
 }data[];
 int map[];
 int pool;
 void addedge(int s,int e,int v)
 {
     int t=map[s];
     data[pool++]=edge(e,v,t);
     map[s]=pool-;
 }
 int mset[];
 int find(int k)
 {
     if (mset[k]==-) return k;
     return mset[k]=find(mset[k]);
 }
 void uion(int a,int b)
 {
     int aa=find(a);
     int bb=find(b);
     mset[aa]=bb;
 }
 struct _que
 {
     int a,b;
     _que(int q=,int w=){a=q;b=w;}
 };
 vector<vector<_que> > ques;
 vector<int > ans;
 int ifv[];
 int dis[];
 int anc[];
 void tar(int cur)
 {
     ifv[cur]=;
     anc[cur]=cur;
     int p=map[cur];
     while (p!=-)
     {
        if (!ifv[data[p].d])
        {
            dis[data[p].d]=dis[cur]+data[p].v;
            tar(data[p].d);
            uion(cur,data[p].d);
            anc[find(cur)]=cur;
        }
         p=data[p].next;
     }
     ifv[cur]=;
     for (int i=;i<(int)ques[cur].size();++i)
     {
         if (ifv[ques[cur][i].a]==)
             ans[ques[cur][i].b]=dis[cur]+dis[ques[cur][i].a]-*dis[anc[find(ques[cur][i].a)]];
     }
 }
 int main()
 {
     int T;
     scanf("%d",&T);
     while (T--)
     {
         ques.clear();
         pool=;
         memset(map,-,sizeof map);
         memset(ifv,,sizeof ifv);
         memset(mset,-,sizeof mset);
         scanf("%d%d",&n,&m);
         ques.resize(n);
         int s,e,v;
         for (int i=;i<n-;++i)
         {
             scanf("%d%d%d",&s,&e,&v);
             addedge(s-,e-,v);
             addedge(e-,s-,v);
         }
         dis[]=;
         ans.resize(m);
         for (int i=;i<m;++i)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             --u;--v;
             ques[u].push_back(_que(v,i));
             ques[v].push_back(_que(u,i));
         }
         tar();
         for (int i=;i<(int)ans.size();++i)
         {
             printf("%d\n",ans[i]);
         }
     }
 }