（一）使用sklearn做各种回归

#申明，本文章参考于 https://blog.csdn.net/yeoman92/article/details/75051848

import numpy as np
import matplotlib.pyplot as plt

# 生成数据
def gen_data(x1, x2):
    y = np.sin(x1) * 1/2 + np.cos(x2) * 1/2 + 0.1 * x1
    return y

def load_data():
    x1_train = np.linspace(0, 50, 500)
    x2_train = np.linspace(-10, 10, 500)
    data_train = np.array([[x1, x2, gen_data(x1, x2) + np.random.random(1) - 0.5] for x1, x2 in zip(x1_train, x2_train)])
    x1_test = np.linspace(0, 50, 100) + np.random.random(100) * 0.5
    x2_test = np.linspace(-10, 10, 100) + 0.02 * np.random.random(100)
    data_test = np.array([[x1, x2, gen_data(x1, x2)] for x1, x2 in zip(x1_test, x2_test)])
    return data_train, data_test

train, test = load_data()
# train的前两列是x，后一列是y，这里的y有随机噪声
x_train, y_train = train[:, :2], train[:, 2]
x_test, y_test = test[:, :2], test[:, 2]  # 同上，但这里的y没有噪声

# 回归部分
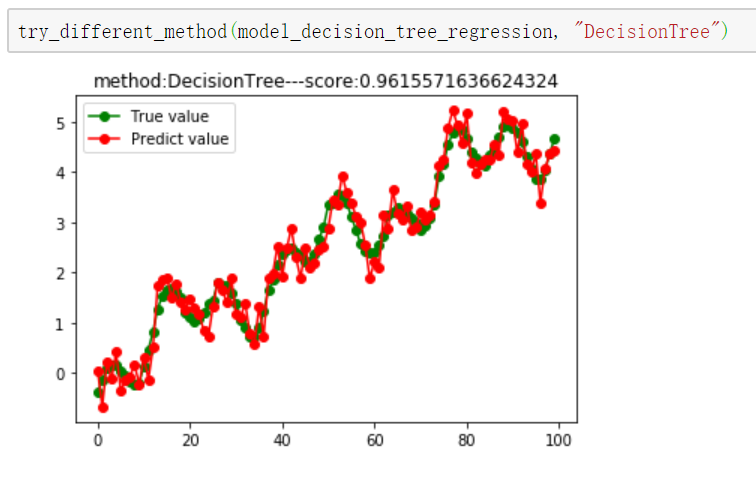
def try_different_method(model, method):
    model.fit(x_train, y_train)
    score = model.score(x_test, y_test)
    result = model.predict(x_test)
    plt.figure()
    plt.plot(np.arange(len(result)), y_test, "go-", label="True value")
    plt.plot(np.arange(len(result)), result, "ro-", label="Predict value")
    plt.title(f"method:{method}---score:{score}")
    plt.legend(loc="best")
    plt.show()

# 方法选择
# 1.决策树回归
from sklearn import tree
model_decision_tree_regression = tree.DecisionTreeRegressor()

# 2.线性回归
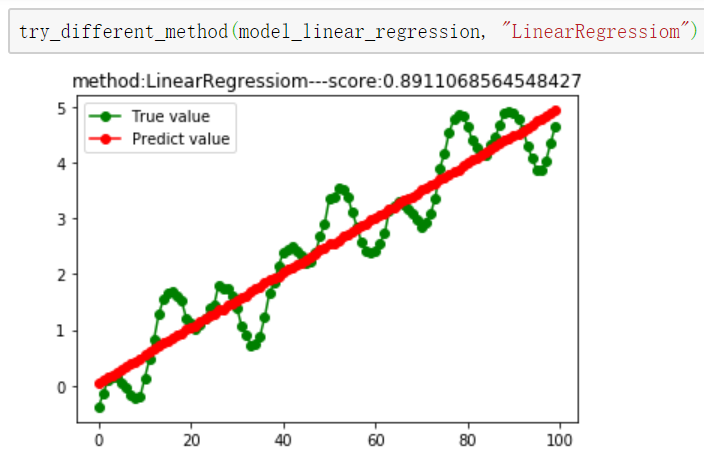
from sklearn.linear_model import LinearRegression
model_linear_regression = LinearRegression()

# 3.SVM回归
from sklearn import svm
model_svm = svm.SVR()

# 4.kNN回归
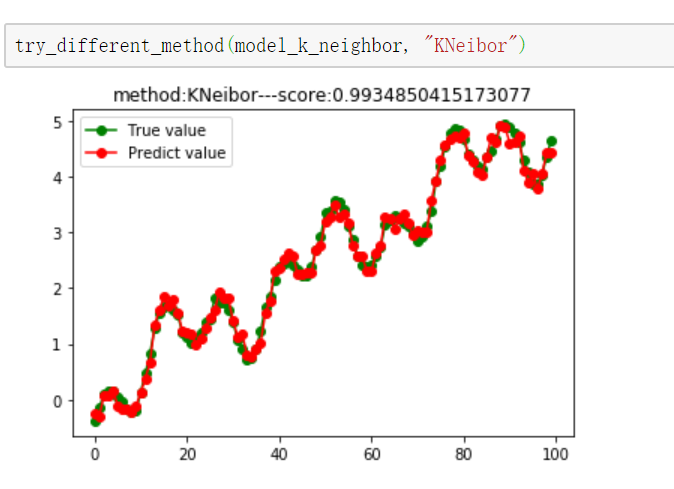
from sklearn import neighbors
model_k_neighbor = neighbors.KNeighborsRegressor()

# 5.随机森林回归
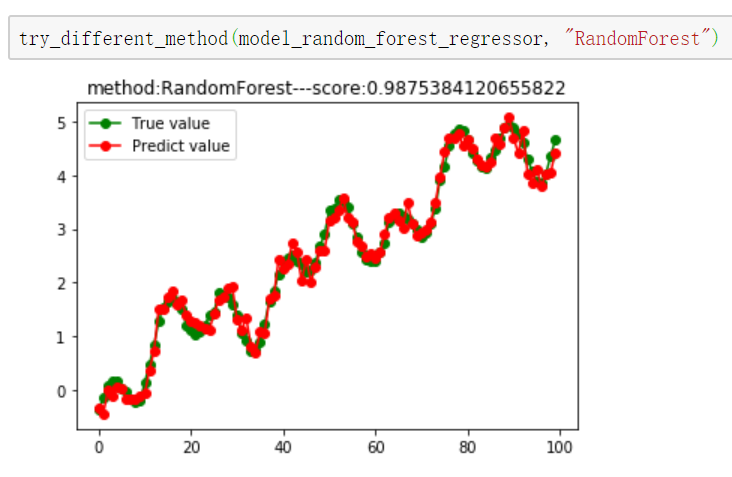
from sklearn import ensemble
model_random_forest_regressor = ensemble.RandomForestRegressor(n_estimators=20)  # 使用20个决策树

# 6.Adaboost回归
from sklearn import ensemble
model_adaboost_regressor = ensemble.AdaBoostRegressor(n_estimators=50)  # 这里使用50个决策树

# 7.GBRT回归
from sklearn import ensemble
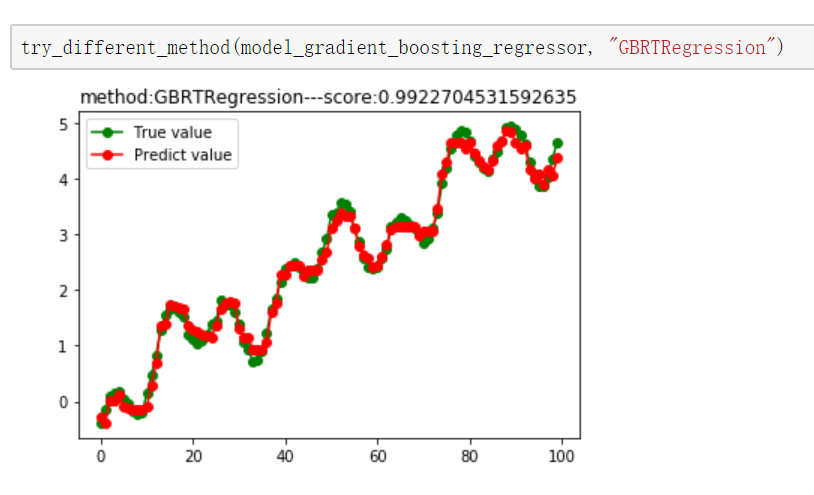
model_gradient_boosting_regressor = ensemble.GradientBoostingRegressor(n_estimators=100)  # 这里使用100个决策树

# 8.Bagging回归
from sklearn import ensemble
model_bagging_regressor = ensemble.BaggingRegressor()

# 9.ExtraTree极端随机数回归
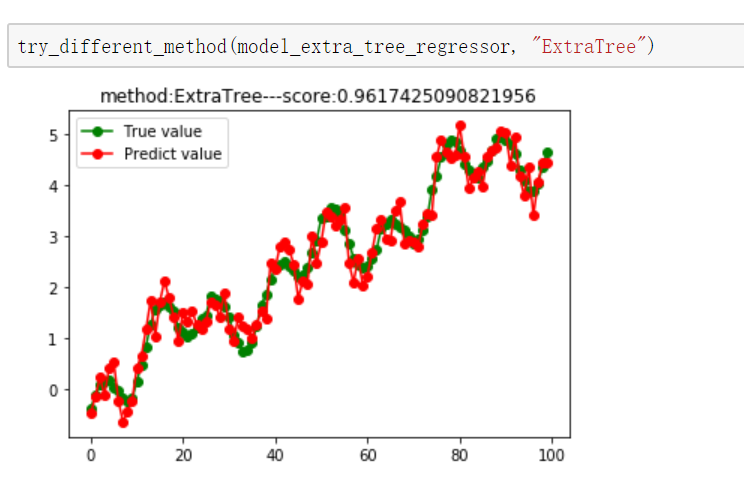
from sklearn.tree import ExtraTreeRegressor
model_extra_tree_regressor = ExtraTreeRegressor()