UVa 10213 How Many Pieces of Land ? (计算几何+大数)欧拉定理

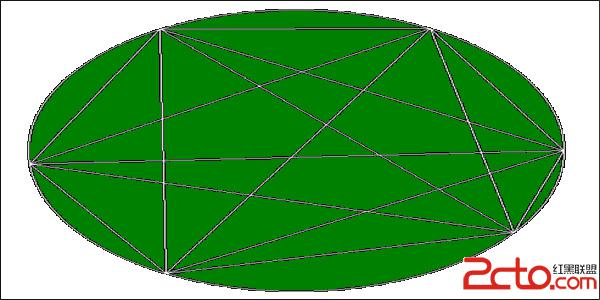
题意：一块圆形土地，在圆周上选n个点，然后两两连线，问把这块土地分成多少块？

析：这个题用的是欧拉公式，在平面图中，V-E+F=2，其中V是顶点数，E是边数，F是面数。对于这个题只要计算V和E就好。

我们从一个顶点开始枚举对角线，这条线左边有 i 个点，那么右边有 n-i-2 个点，那么两边的连线在这条对角线上形成 i * (n-i-2) 个交点，得到 i * (n-i-2) + 1条线段，然而每个交点，

重复计算了四次，每条线段被重复计算了二次，所以总数就是，，V 加 n 的意思就是加上原来的 n 个顶点，E 加 2n的意思就是，

先加原来 n 个点相邻的边数，然后再加上这个椭圆被这个圆分成的n条边，最后就是在总面数再减去那一个“无限面”。这个公式不要用循环来算，要化简公式，最后结果还是挺简单的。

ans = n * (n-1) * (n-2) * (n-3)/24 + n * (n-3)/2 + n + 1。

代码如下：

import java.math.BigInteger;
import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		Scanner cin = new Scanner(System.in);
		int T;
		T = cin.nextInt();
		for(int i = 0; i < T; ++i){
			BigInteger n = cin.nextBigInteger();
			BigInteger n1 = n.subtract(BigInteger.ONE);
			BigInteger n2 = n1.subtract(BigInteger.ONE);
			BigInteger n3 = n2.subtract(BigInteger.ONE);

			BigInteger a = n.multiply(n1).multiply(n2).multiply(n3).divide(BigInteger.valueOf(24));
			BigInteger b = n.multiply(n3).divide(BigInteger.valueOf(2));
			BigInteger ans = a.add(b).add(n).add(BigInteger.ONE);
			System.out.println(ans);
		}
	}

}

原文链接：http://www.cnblogs.com/dwtfukgv/p/5845746.html