神奇的魔方阵--(MagicSquare)(1)

本篇文章只对奇数阶以及偶数阶中阶数n = 4K的魔方阵进行讨论.下面就让我们进入正题:

1 :魔方阵的相关信息:(百度百科)

https://baike.baidu.com/item/%E9%AD%94%E6%96%B9%E9%98%B5/10973743?fr=aladdin

2 :奇数阶和偶数阶魔方阵的排列规律.(源自百度百科)  (可跳至第三部分)

    2.1 :奇数阶魔方阵的排列规律如下：

　　⑴ :将1放在第一行中间一列；

　　⑵ :从2开始直到n×n止各数依次按下列规则存放；每一个数存放的行比前一个数的行数减1，列数加1（例如上面的三阶魔方阵，5在4的上一行后一列；

　　⑶ :如果上一个数的行数为1，则下一个数的行数为n（指最下一行）；例如1在第一行，则2应放在最下一行，列数同样加1；

　　⑷ :当上一个数的列数为n时，下一个数的列数应为1，行数减去1。例如2在第3行最后一列，则3应放在第二行第一列；

　　⑸ :如果按上面规则确定的位置上已有数，或上一个数是第一行第n列时，则把下一个数放在上一个数的下面。例如按上面的规定，4应该放在第1行第2列，

　　     但该位置已经被占据，所以4就放在3的下面。

 

    2.2 :阶数为n = 4K 的魔方阵的排列规律如下：

　　(1) :先将整个方阵划分成k*k个4阶方阵，然后在每个4阶方阵的对角线上做记号；

　　(2) :由左而右、由上而下，遇到没有记号的位置才填数字，但不管是否填入数字，每移动一格数字都要加1；

　　(3) :自右下角开始，由右而左、由下而上，遇到没有数字的位置就填入数字，但每移动一格数字都要加1。

 

3 :排列规律的解读,代码实现以及实验结果( ar 二维数组 ,ROW ==行,  COL ==  列)

　3.1 :奇数阶魔方阵(n = 2*K + 1)

　奇数阶魔方阵的排列规律主要有以下三点:

 　　3.1.1) : 数字1的位置是确定的,摆放在第一行中间的位置,即:  ar[0][COL/2] == 1;

 

 　　3.1.2)(重点)  :假设当前摆放的数行列下标为 [preRow][preCol] , 则下一个数的摆放的位置的下标应为[preRow - 1] [preCol + 1] ,注意在这里(preRow - 1)

　　　　　  以及(preCol + 1)的值都有可能越界. 因此,需要对变化后的值进行操作.我们以ROW＝COL＝３为例，假设上一个值的下标为 [0][3] ,

　　　　      那么下一个值的下标应为[2][1] ,他们与(preRow - 1)以及(preCol + 1)

　　　　　  即 [0 - 1][3 + 1]的关系,为[(-1 + 3)%3] [(3+1+3)%3], 即[(preRow - 1+ ROW)%ROW][(preCol + 1+ COL)%COL].

　　　　　  图示:

 

　　　    　　,

　　　　　　2的摆放位置的下标应为[(0 -1 + 3)%3][(1+1)%3] == [2][2] ,

　　　　　　即:  

 

　　 3.1.3) : 若将要摆放的位置已有值存在,则将该值排放在上一个值的下一行.

　　　　　　例如:以三阶魔方阵为例: 按照相应的规则摆放1,2,3

                       ,

　　　　　　要摆放4的位置的下标通过计算可以得出是[0][1],但是该位置已有数值1,因此4要摆放在3的下一行,即[preRow - 1][preCol],

　　　　　　同时用3.1.2的方法对[preRow-1]进行 防越界处理:   [(preRow - 1 + ROW)%ROW][preCol]. 

　　　　代码如下:

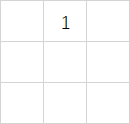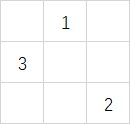#include<assert.h>
#include<stdio.h>
void Magic_Square_1()
{
#define ROW 3
#define COL ROW   //   等价于 #define COL 3
    assert(ROW % 2 != 0);
    if (ROW % 2 == 0)//ROW & ! == 1 判断是否为奇数  &(只有全为1,才为1)
    {
        return;
    }
    int preRow = 0;  //记录上一个数的行坐标
    int preCol = 0;  //记录上一个数的列坐标
    int ar[ROW][COL] = {};
    ar[0][COL / 2] = 1;  //先放1
    preRow = 0;
    preCol = COL / 2;
    for (int i = 2; i <= ROW * COL; i++)//1已经放入所以从2开始进行
    {
        if (ar[(preRow - 1 + ROW) % ROW][(preCol + 1) % COL] == 0)
            //判断上一个数的上一行下一列是否有值若没有则放入当前的i
        {
            preRow = (preRow - 1 + ROW) % ROW;
            preCol = (preCol + 1) % COL;
        }
        else
        { // 若有则i放在上一个数的下一行.
            preRow = (preRow + 1) % ROW;
        }
        ar[preRow][preCol] = i;
    }
    for (int i = 0; i < ROW; i++)//打印
    {
        for (int j = 0; j < COL; j++)
        {
            printf("%3d", ar[i][j]);
        }
        printf("\n");
    }
#undef ROW     //取消定义
#undef COL
}
int main()
{
　　Maagic_Square_1();
　　return 0;
}

　　运行结果:

　　

 

3.2 :偶数阶魔方阵( n = 4*K )

　偶数阶魔方阵的排列规律主要有以下两点:(以8阶为例)

　　 3.2.1) : 先将 1 - ROW*COL 的值按从上到下,从左到右的顺序依次填入.接着将魔方阵分成k*k (在该例 k = 2)个4阶魔方阵,并将4阶魔方阵的对角线的数值取出(如下图带颜色部分的数值).

　　 3.2.2) : 将取出来的值按照从大到小的顺序(或从小到大的顺序)排好,从二维数组的[0][0]下标开始(从二维数组[ROW - 1][COL - 1]的位置开始) 依次填入到数组中空白的位置.

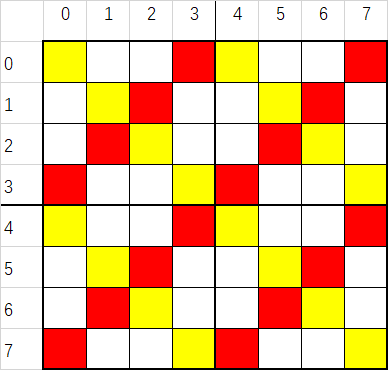
　    (重点)排列n= 4*k 阶的魔方阵的关键是取出各个四阶魔方阵的对角线的元素.我们可以发现:所有在对角线的元素的行列下标只差都满足一定的规律:

　　  即 |row - col|(绝对值) % 4 == 0 (对应图中黄色部分)或者(row + col)%4 == 3(对应图中红色部分) .同时我们可以定义一个数组br[ROW*ROW/2],

　　  在第一步填入数据时对其行列下标进行判断,若满足对角线元素下标的特点,直接将数值存放到br中,同时对二维数组相应的位置赋零值.

　　  这样br 中的数就是从小到大排列的,只需要在第二步时从二维数组ar 的ar[ROW - 1][COL - 1]的位置开始,

依次将数组br中的值填入到数组中空白的位置.

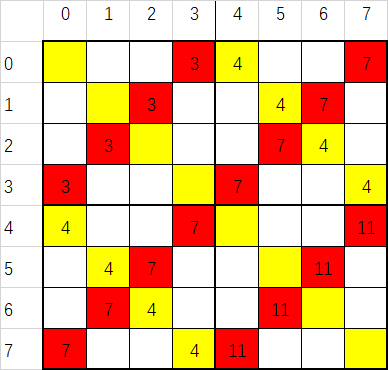
　　    代码如下:

#include<stdio.h>
#include<assert.h>
void Magic_Square_4K()
{
#define ROW 8
#define COL ROW
    int ar[ROW][COL] = {};
    int br[ROW*ROW/2] = {};//用来存储4阶方阵对角线元素.
    int num = 1;//从1开始填入
    int k = 0;//数组br下标.
    for (int i = 0; i < ROW; i++)
    {
        for (int j = 0; j < COL; j++)
        {
        if((i-j)%4==3||(i-j)%4==0|| (j - i) % 4 == 3 || (j - i) % 4 == 0)
        {//先控制对角线元素为零,并将应该填在对角线的这些数记录到br中.
            br[k] = num;
            k += 1;
            ar[i][j] = 0;
        }
        else
        {
            ar[i][j] = num;
        }
        num++;
        }
    }
    int tag = 0;
    for (int i = ROW - 1; i >= 0; i--)//将br中的数按照顺序,从ar[ROW-1][COl-1]开始对ar中为零的元素赋值.
    {
        for (int j = COL - 1; j >= 0; j--)
        {
            if (ar[i][j] == 0)
            {
                ar[i][j] = br[tag];
                tag += 1;
            }
        }
    }

    for (int i = 0; i < ROW; i++)//打印
    {
        for (int j = 0; j < COL; j++)
        {
            printf("%4d", ar[i][j]);
        }
        printf("\n");
    }
#undef ROW
#undef COL
}
int main()
{
    Magic_Square_4K();
    return 0;
}

　  　运行结果:

　　

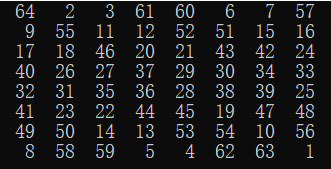
未完待续...