【Notes_2】现代图形学入门——向量与线性代数

向量与线性代数

点乘和叉乘

Dot Multiplication

点乘在图形学的应用

(1) 求两个向量之间的夹角:

$$\cos(\theta) = \frac{(\vec{a} \cdot \vec{b})}{\lVert a \lVert \lVert b \lVert}$$

可以判断两个向量的距离、分向量与判断向量前后



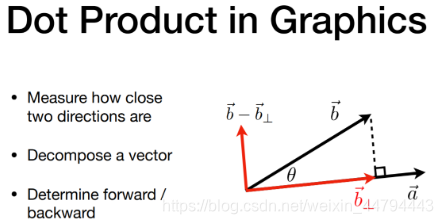
(2) 投影

一个向量在另一个向量上的投影

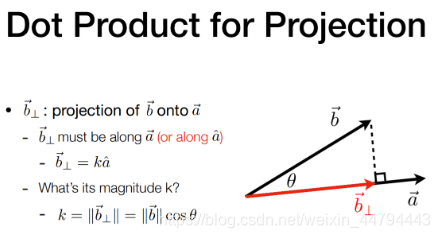
Cross Product

[1] 右手坐标系



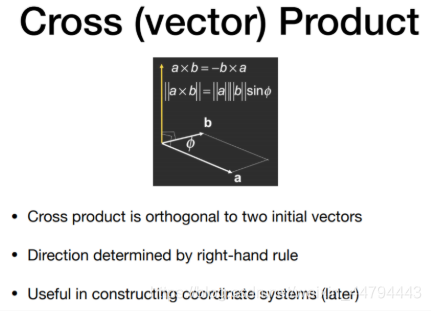
右手坐标系

叉乘在图形学中的应用

(1) 判断一个向量在另一个向量的左右，叉乘为正(与右手方向一致)，则为目标在自己右方，反之亦然；

(2) 在性质(1)的基础上，如果一个点在包围他的所有线的同一侧，那么可以说明该点在这个图形内，反之亦然。

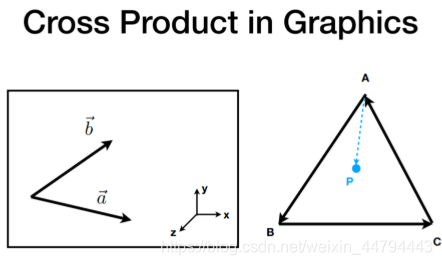
矩阵

矩阵转置与逆

(1) 矩阵A、B乘积的转置等于B的转置矩阵乘A的转置矩阵

\[(AB)^T=B^TA^T
\]

(2) 矩阵AB的逆等于B的逆乘A的逆

\[(AB)^{-1} = B^{-1}A^{-1}
\]