Redis5设计与源码分析读后感（三）跳跃表

一、引言

　　有序集合在日常开发中相当常见，比如做排名等相关的功能，肯定要用到排序的功能，那么常见底层实现有很多种：

数组：不便于元素的插入和删除
链表：查询效率低，需要遍历所有元素
平衡树OR红黑树：性能高但是实现复杂

　　所以这里就引出了本文的主角：

跳跃表 ：性能堪比红黑树，但实现相对简单得多

二、跳跃表简介

　　首先，学习跳跃链表我们先要明白一个概念：

　　有序链表：所有元素以递增或者递减方式有序排列的数据结构，每个节点都有指向下个节点的next指针，最后一个节点的next指针指向NULL。

　　PS：有序链表的修改操作基本不耗时间，耗时主要在查找元素上面。

　　跳跃表：由于链表结构的耗时操作主要在于查找元素上，跳跃表则使用空间换时间的思想，将有序链表中的部分节点分层，每一层都是一个有序链表。

　　查找过程：先从最高层开始向后查找，当达到某个节点时，如果next节点值大于要查找的值或next指针指向NULL，则从当前节点下降一层继续向后查找。

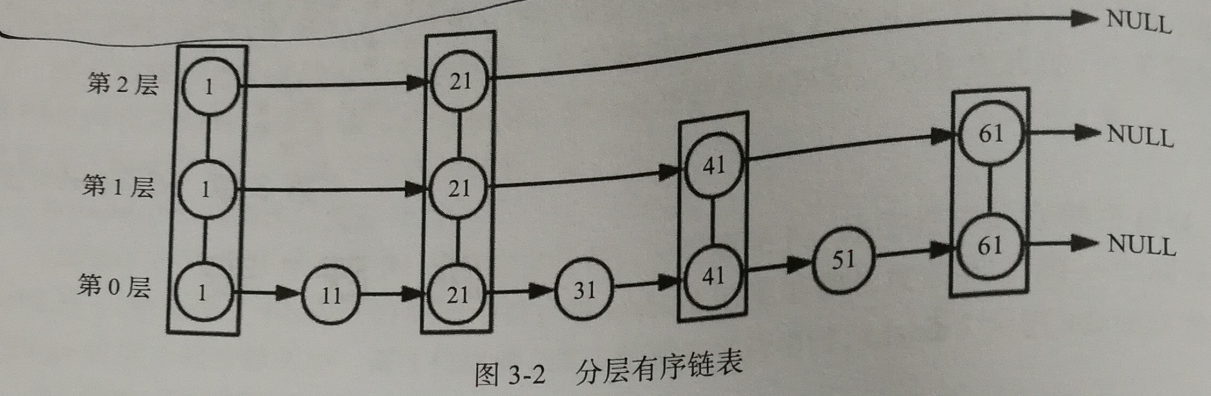
　　特性：

跳跃表由很多层组成
头节点（header）中有个64层的结构，每层包含指向本层下个节点的指针（forward）和之间跨越的节点个数跨度（span）
除去头节点外，层数最高的节点层高为跳跃表的高度
每一层都是有序链表，数据递增
除头节点外，一个元素在上层出现时，则一定会在下层有序链表中出现
跳跃表每层的最后一个节点指向NULL，表示本层结束
跳跃表有一个tail指针，指向跳跃表的最后一个节点
最底层的有序链表包含所有节点，最底层的节点个数为跳跃表的长度（不包括头节点）
每个节点包含一个后退指针，头节点和第一个节点指向NULL，其他节点指向最底层的前一个节点

排序规则：

按分值【score】从小到大排序
分值相同时根据成员内容【member即ele储存的字符串值】的字典序进行排序。

三、跳跃表结构

　　我们结合一张图来分析：

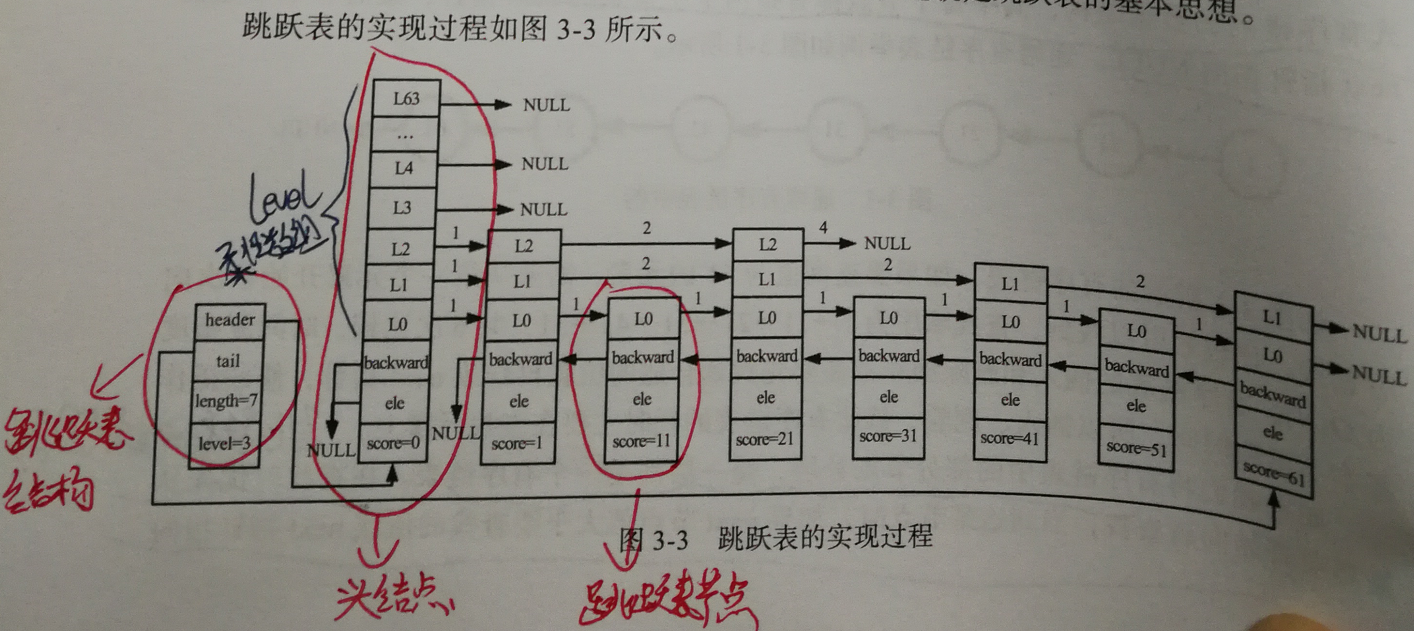
跳跃表节点【zskiplistNode】

ele ：用于储存字符串类型的数据
score ：用于储存排序的分值
backward ：后退指针，指向当前节点最底层的前一个结点，头节点和第一个节点指向NULL
level ：柔性数组，每个节点的数组长度不一样，根据生成时节点的层高来决定【比如当前节点层高为3，则level数组的长度也为3，即有3层存在此节点】，每项包含以下两个元素：
- forward ：指向本层的下一个节点，尾节点指向NULL
- span ：跨度，即本结点与forward指向的节点，之间的元素个数

跳跃表结构【zskiplist】

header ：指向跳跃表头结点，头结点的level数组元素个数为64，且不储存任何member和score值，ele为NULL，score为0，也不计入跳跃表总长度。
tail ：指向跳跃表尾节点。
length ：跳跃表的长度，表示除头结点之外的节点总数。
level ：跳跃表的高度。

四、创建跳跃表

计算节点层高

层高的最小值为1，最大值为64。
通过zslRamdomLevel函数随机生成1~64的值，作为新建节点的高度，值越大出现概率越低。

创建跳跃表节点

所有待创建节点的层高、分值和内容都已确定。
申请内存，内存大小为zskiplistNode的内存大小和level个zskiplistLevel的内存大小之和。

创建头节点

头节点是跳跃表中第一个插入的节点。
不储存集合的member信息，即不储存具体字符串内容。
level数组的每项forward都为NULL，span都为0。

创建步骤

创建跳跃表结构体对象zsl。
将zsl的头节点指针指向新创建的头节点。
跳跃表层高初始化为1，长度初始化为0，尾节点指向NULL。

五、插入节点

查找要插入的位置

　　为了找到需要更新的节点，我们需要以下两个长度为64的数组来辅助操作：

update[ ] ：记录每层需要更新的节点。
rank[ ] ：记录当前层从header节点到update[ i ]节点所经历的步长，更新update[ i ]的span和设置插入节点的span时用到。

调整跳跃表高度

　　由于插入节点的高度是随机的，上面的例子中我们要插入一个level为3的节点，而插入前跳跃表的高度为2，则我们需要调整跳跃表的高度【只发生在插入节点高于当前跳跃表高度时】：

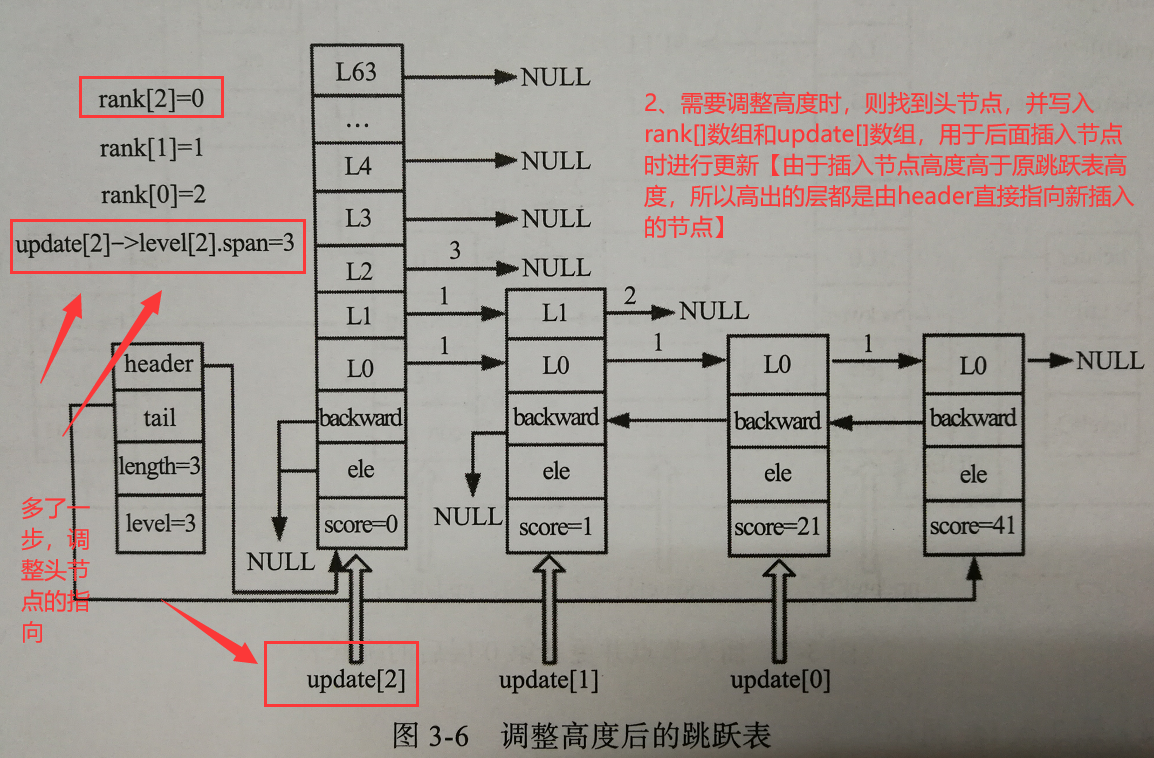
插入节点

　　经过前面两步，设置好update[ ]和rank[ ]后，我们就可以进行插入节点的操作了：

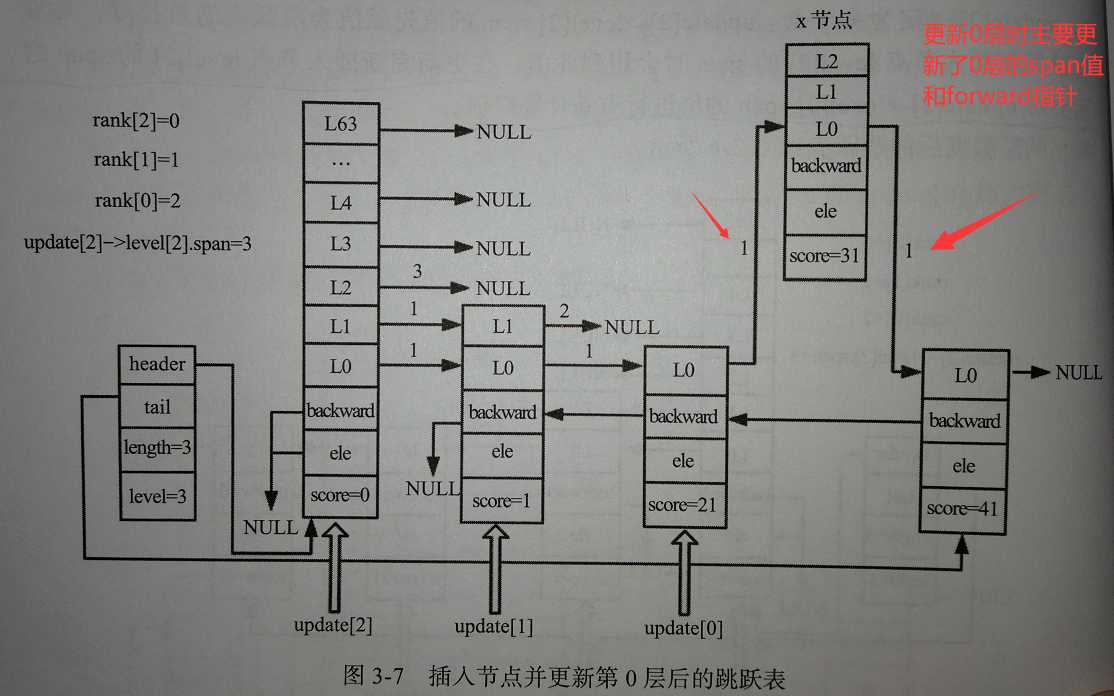
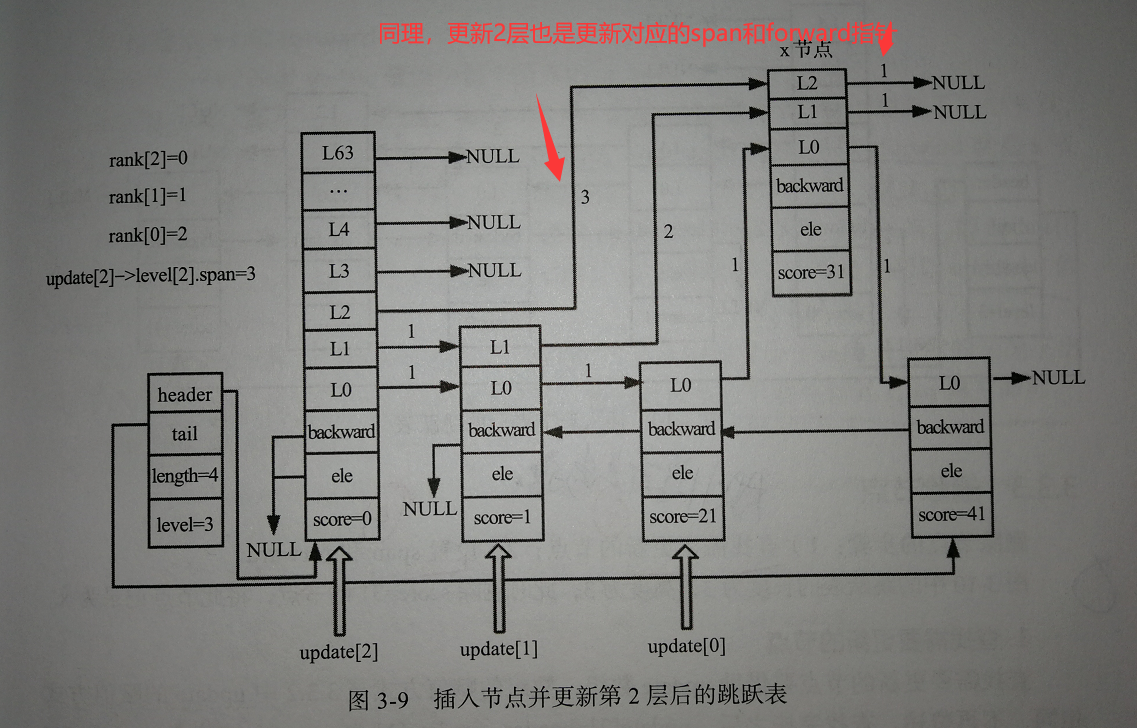
　　我们可以看出，在插入节点操作时，主要还是在更新被插入节点的level柔性数组，然后再处理好每个节点对应层高与新插入节点之间的关系。

调整backward

　　根据update[ ]的赋值过程，新插入节点的前一个节点一定是update[0]，由于每个节点的后退指针【backward】只有一个，与此节点的层数无关，则：

被插入节点的backward指向update[0]
如果新插入的节点是最后一个节点，需要指定跳跃表结构的tail【尾节点】指向新插入的节点
更新跳跃表的长度+1

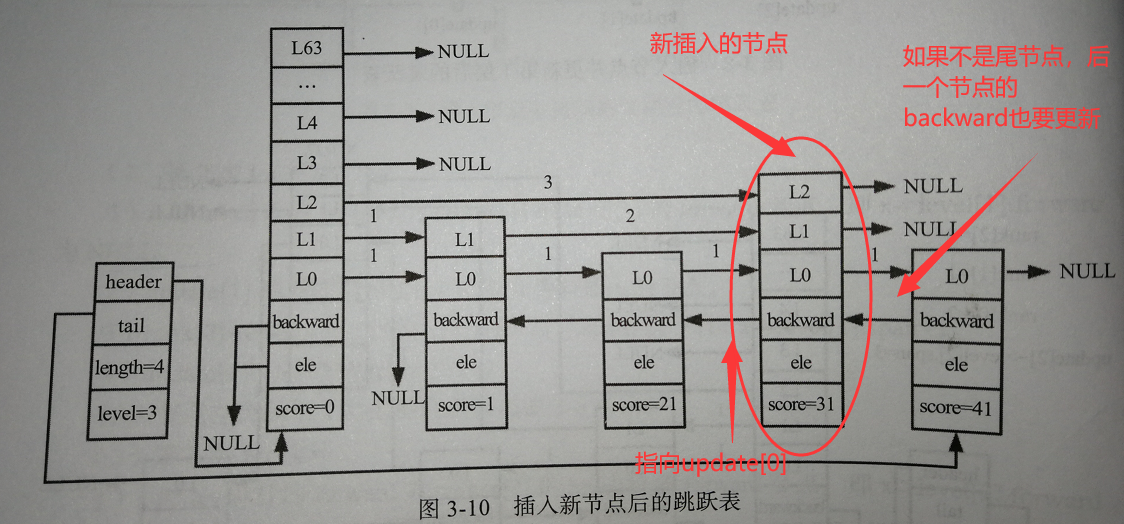
六、删除节点

查找需要更新的节点

　　查找方法与上面类似，也是需要借助update[ ]数组进行记录需要更新的节点：

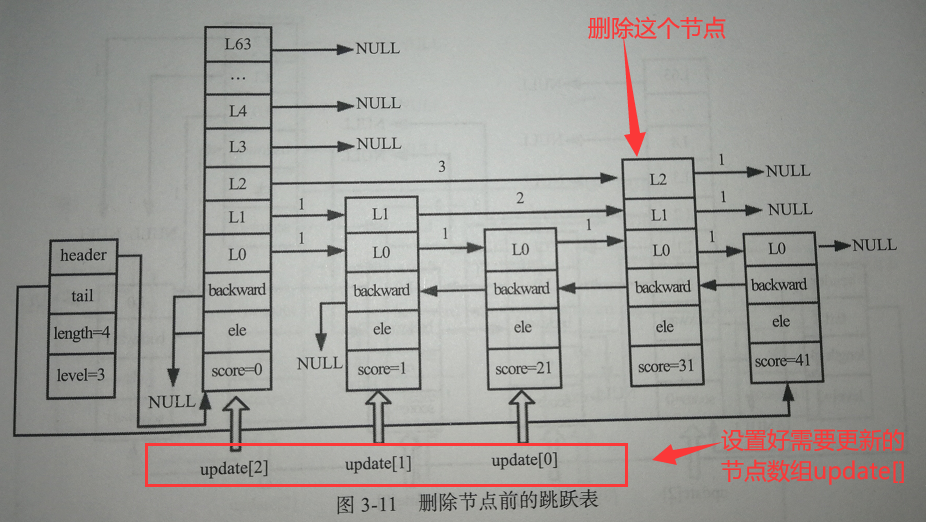
设置span和forward

　　删除节点前需要设置update[ ]数组中每一个节点的span和forward，有以下几种情况【下面以x来代表需要删除的节点】：

① x的第i层的span值为a，update[i]的第i层的span值为b，且update[i]第i层的forward为x时 ：
- update[i]的第i层的span ：a+b-1
- update[i]的第i层的forward ：x节点第i层的forward
② update[i]第i层的forward不为x时 ：
- update[i]的第i层span ：原span-1

更新backward、跳跃表长度、跳跃表高度

更新backward

x不为最后一个节点 ：把0层后一个节点的backward设置成x节点的backward
x为最后一个节点 ：把跳跃表结构的tail指向x的backward

更新跳跃表长度

　　删除1个节点，跳跃表长度-1

更新跳跃表高度

　　如果x节点是最高节点，且没有其他节点与之同高，则跳跃表高度-1

七、删除跳跃表

从头结点的第0层开始，通过forward指针逐步向后遍历
每遇到一个节点便将其内存释放
当所有节点的内存都被释放以后，释放跳跃表对象，此时删除跳跃表完成

八、跳跃表的应用

　　跳跃表主要应用于有序集合的底层实现(有序集合的另一种实现方式为压缩列表)。

Redis的配置文件中关于有序集合底层实现的两个配置

zset-max-zip-list-entries 128 ：zset采用压缩列表时，元素个数最大值，默认值为128。
zset-max-zip-list-value 64 ：zset采用压缩列表时，每个元素的字符串长度最大值，默认值为64。

插入第一个元素

　　插入第一个元素时，会判断以下两个条件：

zset-max-zip-list-entries的值是否等于0。
zset-max-zip-list-value小于要插入元素的字符串长度。

　　满足任一条件Redis就会采用跳跃表作为有序集合的底层实现，否则采用压缩列表作为底层实现。

　　PS：一般情况下，默认还是使用压缩列表作为底层实现的。

再次插入元素

　　再次插入元素，会判断以下两个条件：

zset中元素的个数大于zset-max-zip-list-entries。
插入元素的字符串长度大于zset-max-zip-list-value。

　　满足任一条件Redis便会将zset的底层实现由压缩列表转为跳跃表。

　　PS：zset在转为跳跃表之后，即使元素被删除，也不会重新转换为压缩列表。

　　PS：插入、查找、删除操作的平均时间复杂度均为O(logN)，主要时间消耗在定位元素上。