预设型 DP

预设型 DP

《美好的一天》--青春学概论

한 잔 술에 취해 잠긴 목엔
沉醉于一杯酒
갈라지는 목소린 다시
带着沙哑的嗓音
두 잔 자기 전엔 기분 좋음
入睡前饮下第二杯让心情愉悦
알 수 없는 세상에 빠져
陷入不可预知的世界
세 잔 또 네 잔 술에 빠진
又沉醉于第三杯第四杯
세상과 취해가는 사람들
这个世界还有酒醉的人们
다시 또다시 기분 좋음
再一次变得心情愉悦
다 노래를 부른다
大家放声高歌
라라랄라랄라라
啦~
라라랄라랄라라
啦~
라라랄라랄라라
啦~
목소리는 다시
再次高歌
라라랄라랄라라
啦~
라라랄라랄라라
啦~
라라랄라랄라라
啦~
솔직히 우리는
说实话
친구 그 이상도
我们的关系
이하도 아닌데
似友情却非友情
가끔 네가
偶尔会觉得
너무 예뻐 보여
你很美丽
이게 말이 돼
这像话吗
특히 오늘 같은
特别是在今天
날이면 더더욱
这样的日子
지금 네가 쳐다보고
你现在正在
있는 손거울
看的镜子
그게 내 얼굴이었으면 하는
如果是我的脸就好了
말도 안 되는 생각
有着这样不像话的想法
널 자기라고 부를 날이 올까
会有一天我能叫你亲爱的吗
언젠가 미안 취한 것 같아 나
会是什么时候呢 对不起我好像喝醉了
그래도 좋은 날이니까
即使这样也是好日子
뭐 이 정도는 괜찮잖아
应该没有关系吧
한 잔 술이 들어가니까
饮下一杯酒
두 잔 새벽 세 시잖아
第二杯已经到了凌晨三点
괜찮아 첫차 뜰 때까지
没关系 直到清晨来临
같이 있어 줄게
我会一直
네 곁에
在你左右
하루 밤 새워 마신 술이
熬夜饮下的酒
이틀 휘청거리게 해도
即使会让第二天眩晕
괜찮아 기대 내 어깨에
没关系 靠在我的肩膀上
난 그림자처럼
我会像影子般
말없이 항상 네 옆에
默默无语 一直陪伴你身边
세 잔 또 네 잔 술에 빠진
又沉醉于第三杯第四杯
세상과 취해가는 사람들
这个世界还有酒醉的人
다시 또다시 기분 좋음
再一次变得心情愉悦
다 노래를 부른다
大家放声高歌
라라랄라랄라라
啦~
라라랄라랄라라
啦~
라라랄라랄라라
啦~
목소리는 다시
再次高歌
라라랄라랄라라
啦~
라라랄라랄라라
啦~
라라랄라랄라라
啦~
오늘의 주인공은 너
你是今天的主角
생일 축하해
生日快乐
동시에 코 앞까지 온
也祝贺你
입대를 축하해
近在眼前的入伍日子
놀리는 건 아냐
不是开玩笑
나도 곧 갈텐데 뭐
我也马上就要去了
신경 쓰지 말고 임마
不要想太多 小子
빈 잔이나 채워
将空杯斟满酒
넌 항상 되고 싶어 했잖아
你不是一直想要成为
진짜 사나이
真正的男人吗
이젠 그 시간이 온 거지
现在这一天来了
나의 둘도 없는 친구 놈인
我独一无二的朋友
너에게도 말이야
你也是一样
오늘은 우리들끼리
今天我们要
끝까지 가는 날이야
一直喝到最后
한 잔 술이 들어가니까
饮下一杯酒
두 잔 새벽 세 시잖아
第二杯已经到了凌晨三点
우리는 아직 젊고
我们正年轻
이 새벽은 길어
这个深夜太长
하나 걱정이 있다면
仅有的担心是
네가 조금 취했다는 정도
你已经微微醉了
하루 밤 새워 마신 술이
熬夜饮下的酒
이틀 휘청거리게 해도
即使会让第二天眩晕
우리는 아직 젊고
我们正年轻
그건 축복이지
那就是祝福
이 노래는 우리를
这是为我们
위한 곡이지
唱的歌
세상은 취해 돌고
在我的世界沉醉旋转
내 두 눈은 감기고
闭上我的双眼
술에 취해 조금 어지럽지만
虽然醉酒让我有些眩晕
이 기분이 난 좋아
但我喜欢这样的心情
네가 생각나는 밤
想起你的夜里
나는 다시 노래를 부른다
我再一次歌唱
라라랄라랄라라
啦~
라라랄라랄라라
啦~
라라랄라랄라라
啦~
목소리는 다시
再次高歌
라라랄라랄라라
啦~
라라랄라랄라라
啦~
라라랄라랄라라
啦~
목소리는 다시 꼬이긴 해도
再次高歌 就算跑调
하나도 안 이상해 괜찮아
没关系 一点也不奇怪
오늘만큼은
今天这样的日子
네가 저녁때 뭘 먹었는지
即使让我看到你晚上吃的什么
보여줘도 괜찮아
也没关系
오늘만큼은
今夜
집에 가는 길에
回家的路
자꾸만 춤을 춰도 괜찮아
就算跳舞也没关系
오늘만큼은
像今天
함께 있으면
在一起的日子
좋은 사람들과의 기분 좋은 날
和美好的人一起度过的让人心情愉悦的日子
오늘만큼은
今天这样
한 잔 술에 취해 잠긴 목엔
沉醉于一杯酒
갈라지는 목소린 다시
带着沙哑的嗓音
두 잔 자기 전엔 기분 좋음
入睡前饮下第二杯让心情愉悦
다 노래를 부른다
大家放声高歌

前言

一种非常神奇的 \(DP\) 方式，可以处理排列计数问题。

例题

DP 搬运工1

题意：给你 \(n,K\) ，求有多少个 \(1\) 到 \(n\) 的排列，满足相邻两个数的 \(\max\) 的和不超过 \(K\) 。答案对 \(998244353\) 取模。

\(n \le 50 , K \le n^2\)

设 \(dp_{i , j , k}\) 表示 前 \(i\) 个数，分成 \(j\) 个连续段，和为 \(k\) 的个数。

我们从大往小里加，保证了每次增加的答案为 \(i\) .

无非分成三种情况：

1. \(i\) 自成一个连续段 : 现在有 \(j - 1\) 个连续段，新加的有 \(j\) 种可能性，因此:

\[dp_{i , j , k} += dp_{i - 1 , j - 1 , k - i} \times j
\]

1. \(i\) 并在一个连续段里，即变为一个连续段的两端。 \(j\) 个连续段，显然有 \(2j\) 种选法，因此:

\[dp_{i , j , k} += dp_{i - 1 , j , k - i} \times 2j
\]

1. \(i\) 连起来两个连续段，最后 \(j\) 段，之前就是 \(j + 1\) 段，那么就是 \(j\) 个空，因此:

\[dp_{i , j , k} += dp_{i - 1 , j + 1 ， k - 2i} \times j
\]

于是我们就得到了 \(dp_{i , j , k}\) .

TexCode

CODE

#include <bits/stdc++.h>
#ifdef Using_Fread
char buf[1 << 20] , *p1 , *p2 ;
#define getchar() ((p1 == p2 && (p2 = (p1 = buf) + fread(buf , 1 , 1 << 20 , stdin) , p1 == p2)) ? EOF : *p1 ++)
#endif
#ifdef linux
#define getchar getchar_unlocked
#define putchar putchar_unlocked
#endif
using namespace std ;
typedef long long ll ;
const int N = 52 ;
const int mod = 998244353 ;
namespace Fast_IO {
	inline ll read() {
		ll x = 0 , f = 1 ;
		char c = getchar() ; 

		while (c < '0' || c > '9') {
			c = getchar() ;
		}

		while (c >= '0' && c <= '9') {
			x = x * 10 + c - '0' ;
			c = getchar() ;
		}

		return x * f ;
	}
	void write(ll x) {
		if (x / 10) write(x / 10) ;
		putchar(x % 10 + '0') ;
	}
} using namespace Fast_IO ; 

int n , K ;
int dp[N][N][N * N] ; 

signed main() {
	#ifdef LOCAL
	freopen("1.in" , "r" , stdin) ;
	freopen("1.out" , "w" , stdout) ;
	#endif
	n = read() , K = read() ;
	if (n == 1) {
		cout << 1 ;
		return 0 ;
	}
	dp[1][1][0] = 1 ; ll val = 1 ; 

	for (int i = 2 ; i <= n ; ++ i) {
		dp[i][i][0] = (val * i) % mod ; val = (val * i) % mod ; 

		for (int j = 1 ; j < i ; ++ j) {
			for (int k = 1 ; k <= i * i ; ++ k) {
				dp[i][j][k] = ((ll)dp[i - 1][j - 1][k] * (ll)j) % mod ;
				dp[i][j][k] = (dp[i][j][k] + (dp[i - 1][j][k - i] * ((2ll * (ll)j) % mod)) % mod) % mod ; 

				if (k >= 2 * i) dp[i][j][k] = (dp[i][j][k] + (ll)((ll)dp[i - 1][j + 1][k - 2 * i] * (ll)j) % mod) % mod ;
			}
		}
	}

	ll ans = 0 ;
	for (int i = 1 ; i <= K ; ++ i) {
		ans = (dp[n][1][i] + ans) % mod ;
	}

	cout << ans << '\n' ;
}

[JOI Open 2016] 摩天大楼

译自 JOI Open 2016 T3 「高層ビル街 / Skyscraper」

题目描述

将互不相同的 \(N\) 个整数 \(A_1, A_2, \cdots, A_N\) 按照一定顺序排列。

假设排列为 \(f_1, f_2, \cdots, f_N\)，要求：\(| f_1 - f_2| + | f_2 - f_3| + \cdots + | f_{N-1} - f_N| \leq L\)。

求满足题意的排列的方案数对 \(10^9+7\) 取模后的结果。

\(N \le 100 , L \le 1000 , A_i \le 1000 (i \in [1 , n])\)

这是好题

先考虑一下 \(O(n^2\sum\limits a_i)\) 的做法:

我们为了处理掉绝对值号，直接将 \(A_i\) 从大到小排序。

如果我们不进行连续段合并，就是说只考虑往两端加的情况，显然是一个钩子状的。

图:

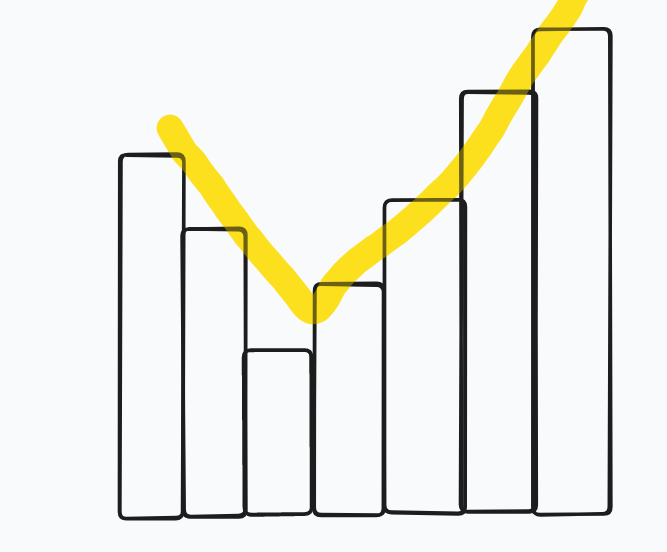
(反正类似吧)

然后我们对于这样的段来说，其答案显然为 \(left + right - 2mid\)

( \(left\) 指最左端值， \(right\) 指最右段值， \(mid\) 指中间段最小的那个数 )

然后如果两个钩子合并的话，图:

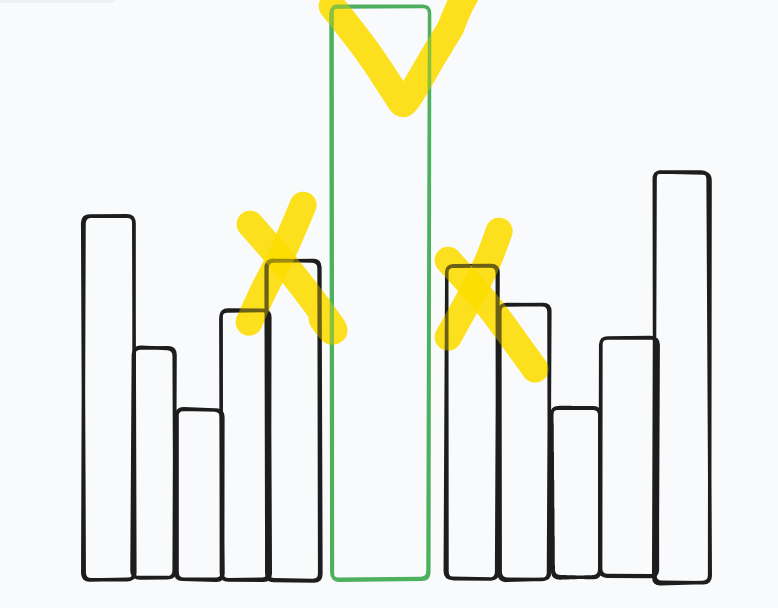
我们就发现中间那个最高的变成左右两个的左端或右端。

那总答案 \(\Delta\) 为 \(2new - left_{right} - right_{left}\)

我们发现只要不是最左端或最右端，那么都会经历一个这样的过程，因此在我们 \(DP\) 的时候，只将区间最左和区间最右的特殊考虑。

具体的，设 \(dp_{i , j , k , d}\) 表示前 \(i\) 个， \(j\) 段 , 答案为 \(k\) , 拥有 \(d\) 个端点( \(1\) 或 \(n\) )。

那如果是合并段：

\[dp_{i , j , k , d} = dp_{i - 1 , j + 1 , k - 2a_i , d} \times j
\]

至于为什么从 \(k-2a_i\) 转移来，就是为了上图中可能的减法(我们不知道那俩数是啥)准备的，非极端点不加入转移。

若是新加段且不为端点：

\[dp_{i , j , k , d} = dp_{i - 1 , j - 1 , k + 2a_i , d} \times j
\]

\(a_i\) 将是 \(a_i\) 所在钩子的最小值， (上面不是算出 \(-2mid\) 吗)。

若是新加段并是端点：

\[dp_{i , j , k , d} = dp_{i - 1 , j - 1 , k + a_i , d - 1} \times(2 - d + 1)
\]

端点只有左右两种情况了吧。为什么从 \(k + a_i\) 转移来是因为其与某个 \(left\) 或 \(right\) 重合，需特殊处理。

若是并在某段两边，且不为端点：

\[dp_{i , j , k , d} = dp_{i - 1 , j , k , d} \times (2j - d)
\]

若是并在某段两边，且为端点：

\[dp_{i , j , k , d} = dp_{i - 1 , j , k + a_i , d - 1} \times (2 - d + 1)
\]

然后我们发现这个 \(DP\) 第三维是要处理到 \(\sum a_i\) 的，因为既有加又有减。

所以时间复杂度是 \(O(n^2 \sum a_i)\) 的，寄了。

然后考虑一下优化哈。有这么个东西叫提前处理答案。

对于一个差分 \(a_{i + 1} - a_i\) 他的贡献。

我们发现对于 \(a_i - a_j (i > j)\) 来说，我们知道这个：

\[a_i - a_j = \sum_{k = j + 1}^{i}a_k - a_{k - 1}
\]

那么只有左右 \(i < k \le j\) 时 \(a_k - a_{k - 1}\) 才被计算。

那么就是说在当 \(a_{i + 1}\) 加入时：

现在共有 \(j\) 个段吧，那么这 \(j\) 个段里每个数都是小于 \(a_{i + 1}\) 的。

那么加入 \(a_{i + 1}\) 以后，很多数并在了 \(j\) 个段的左右两端。

假设段 \(k\) 在左端未处理 \(a_{i + 1}\) 前数为 \(x\) , 第一个在处理完 \(a_{i + 1}\) 后数为 \(y\) 。

显然 \(y > a_{i + 1} > x\) 。

那么 \(y - x\) 的值就有 \(a_{i + 1} - a_i\) 的一份贡献。

再往后，新并在 \(y\) 左的值就不满足条件了。同理， \(k\) 右端第一个新并上的值一样，所有端包括 \(a_{i + 1}\) 所处的端也一样。

那么我们就发现共有 \(2j\) 个位置是符合条件的，是能被贡献上的。当然还要考虑左右极端点，设已有个数为 \(d\) , 所以本差分贡献为 \((2j - d) \times (a_{i + 1} - a_i)\) ( \(j\) 是处理前的段的数量 ) 。

然后就可以得到式子了。 \(DP\) 设计不变，只要将所有的 \(k\) 加减什么数全部改成 \(k_2 =(2j - d) \times (a_{i + 1} - a_i)\) 就可以了。

如果目前的 \(k_2\) 超过 \(L\) 直接不算弃了就行，时间复杂度 \(O(n^2L)\) 。

#include <bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int N = 101 ;
const int M = 1010 ;
const int mod = 1e9 + 7 ; 

int n , m , a[N] ;
int dp[N][N][M][3] ; 

signed main() {
	ios :: sync_with_stdio(0) , cin.tie(0) , cout.tie(0) ;
	cin >> n >> m ; 

	if (n == 1) { // 特判 n = 1
		cout << 1 ; return 0 ;
	}

	for (int i = 1 ; i <= n ; ++ i) cin >> a[i] ; 

	stable_sort(a + 1 , a + n + 1) ;
	dp[0][0][0][0] = 1 ; 

	for (int i = 0 ; i < n ; ++ i) {
		for (int j = 0 ; j <= i ; ++ j) {
			for (int k = 0 ; k <= m ; ++ k) {
				for (int d = 0 ; d <= 2 ; ++ d) {
					ll k2 = 1ll * (2 * j - d) * (a[i + 1] - a[i]) + 1ll * k ;
					if (k2 > m || k2 < 0) continue ;
					if (!dp[i][j][k][d]) continue ; 

					if (j >= 2) dp[i + 1][j - 1][k2][d] = (1ll * dp[i + 1][j - 1][k2][d] + 1ll * dp[i][j][k][d] * (j - 1)) % mod ; // 合并两个区间
					if (j >= 1) dp[i + 1][j][k2][d] = (1ll * dp[i + 1][j][k2][d] + 1ll * dp[i][j][k][d] * (2 * j - d)) % mod ; // 并在一个区间左右且不为端点
					dp[i + 1][j + 1][k2][d] = (1ll * dp[i + 1][j + 1][k2][d] + 1ll * dp[i][j][k][d] * (j + 1 - d)) % mod ; // 重开一个且不为端点

					if (d < 2 && j >= 1) dp[i + 1][j][k2][d + 1] = (1ll * dp[i + 1][j][k2][d + 1] + 1ll * dp[i][j][k][d] * (2 - d)) % mod ; //  并在一个区间左右且为端点
					if (d < 2) dp[i + 1][j + 1][k2][d + 1] = (1ll * dp[i + 1][j + 1][k2][d + 1] + 1ll * dp[i][j][k][d] * (2 - d)) % mod ; // 重开一个且为端点
				}
			}
		}
	}

	ll ans = 0 ; 

	for (int i = 0 ; i <= m ; ++ i) {
		ans = (ans + 1ll * dp[n][1][i][2]) % mod ;
	}

	cout << ans ;
}