机器学习中的两个重要函数--sigmoid和softmax

机器学习中，常常见到两个函数名称：sigmoid和softmax。
前者在神经网络中反复出现，也被称为神经元的激活函数；
后者则出现在很多分类算法中，尤其是多分类的场景，用来判断哪种分类结果的概率更大。

本文主要介绍这两个函数的定义，形态，在算法中的作用，以及两个函数之间的联系。

1. sigmoid函数

1.1. 函数定义

sigmoid函数一类函数的统称，常见的sigmoid函数有：\(y=\frac{1}{1+e^{-x}}\)
它有时也被称为S函数，是因为它的图像显示出来是S形的。

x = np.linspace(-10, 10, 100)
y = 1 / (1 + np.exp(-x))

plt.figure(figsize=(6, 4))
plt.plot(x, y)
plt.title("S-函数")
plt.grid(True)

plt.show()

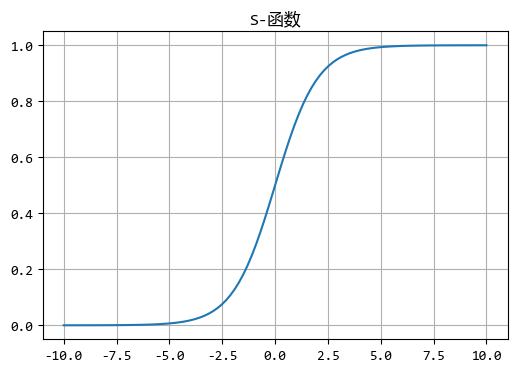
从图形可以看出，S函数的输出会控制在一个有限的范围内（上面的函数是0~1之间），
真是这个特性使得它非常适合表示概率或者用于二分类问题的输出层。

注意，sigmoid函数的输出并不是一定要在区间(0,1)中，
比如还有个常用的S函数：\(tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)，它的的输出区间是(-1,1)。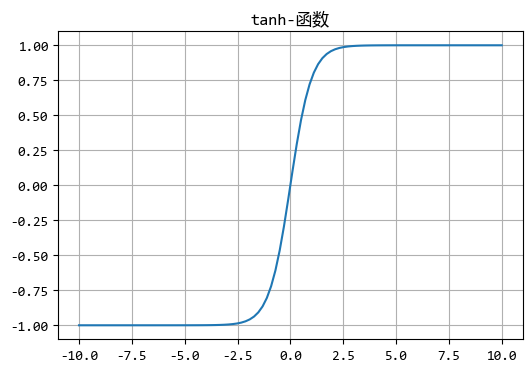

1.2. 应用场景

sigmoid函数的主要使用场景有：

1. 逻辑回归算法：sigmoid函数可用于将线性回归模型的输出转换为概率值，从而用于二分类问题。模型输出的概率值表示了样本属于某一类的可能性。
2. 神经网络的激活函数：它帮助神经网络学习复杂的决策边界，通过非线性转换增加模型的表达能力。
3. 门控机制：在LSTM（长短期记忆网络）等循环神经网络中，sigmoid函数（或其变体）被用作门控机制的一部分，以控制信息的流动。

sigmoid函数在机器学习和早期的深度学习中扮演着重要的角色，尤其是在处理二分类问题和作为神经网络中的激活函数时。
不过，随着深度学习的发展，其他激活函数因其更优越的性能而逐渐取代了sigmoid函数在某些场景下的地位。

2. softmax函数

2.1. 函数定义

接下来介绍softmax函数，softmax函数是一种在机器学习和深度学习中广泛使用的函数，特别是在处理多分类问题的场景中。
而上面介绍的sigmoid函数更多应用在二分类场景。

softmax函数的主要作用是将一个K维向量（通常表示每个类别的原始预测分数）转换成一个元素范围都在(0, 1)之间K维向量，并且所有元素的和为1。
这段话有点抽象，举个例子来说，比如有一个3维向量：\((x_1,x_2,x_3) = (3,1,-2)\)
其中每个元素的值都不在区间(0, 1)中，所有元素的和也不是1。

那么，softmax函数是如何转换的呢？
首先，求出各个元素的exp的和：\(m=e^{x_1}+e^{x_2}+e^{x_3}\)。
然后，将向量\(x\)转换为向量\(y\):\((y_1,y_2,y_3)= (\frac{e^{x_1}}{m},\frac{e^{x_2}}{m},\frac{e^{x_3}}{m})\approx(0.876,0.118,0.006)\)
转换之后的\(y\)向量每个元素的值都在区间(0, 1)中，并且所有元素的和为1。

softmax函数也可以绘制图形。

from mpl_toolkits.mplot3d import Axes3D

def softmax(x0, x1, x2):
    m = np.exp(x0) + np.exp(x1) + np.exp(x2)
    return np.exp(x0) / m, np.exp(x1) / m, np.exp(x2) / m

count = 30
x0 = np.linspace(-10, 10, count)
x1 = np.linspace(-5, 5, count)

y = np.zeros((count, count, 3))
for i0 in range(count):
    for i1 in range(count):
        y[i1, i0, :] = softmax(x0[i0], x1[i1], 1)

xx0, xx1 = np.meshgrid(x0, x1)
plt.figure(figsize=(10, 4))

ax1 = plt.subplot(1, 2, 1, projection="3d")
ax1.plot_surface(xx0, xx1, y[:, :, 0], color="g")
ax1.set_xlabel("$x_0$", color="g")
ax1.set_ylabel("$x_1$", color="g")
ax1.set_zlabel("$y_0$", color="g")

ax2 = plt.subplot(1, 2, 2, projection="3d")
ax2.plot_surface(xx0, xx1, y[:, :, 1], color="r", cstride=1)
ax2.set_xlabel("$x_0$", color="r")
ax2.set_ylabel("$x_1$", color="r")
ax2.set_zlabel("$y_1$", color="r")
ax2.zaxis.labelpad=-1

plt.tight_layout()
plt.show()

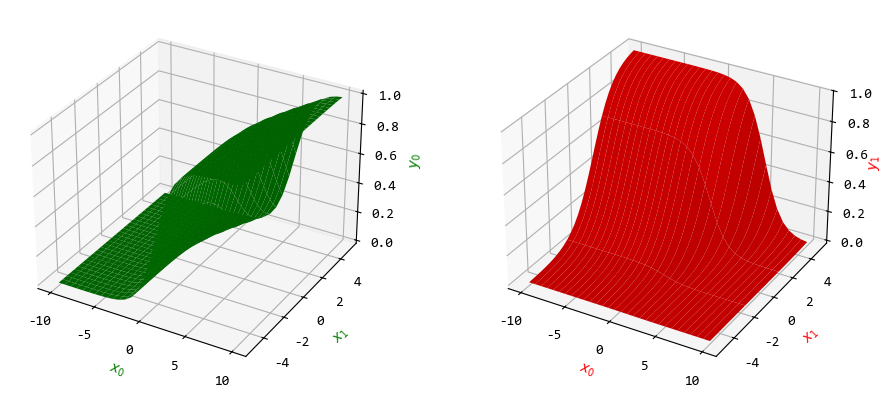
从图中可以看出，\(y_0,y_1\)被映射到区间(0, 1)中。

2.2. 应用场景

softmax函数可以应用在：

1. 多分类问题：它是处理多分类问题时的标准输出层激活函数。能够将模型的原始输出（通常是线性层的输出）转换为概率分布，便于后续使用交叉熵损失函数进行训练。
2. 神经网络的输出层：在构建用于分类任务的神经网络时，常被用作输出层的激活函数。特别是在卷积神经网络（CNN）、循环神经网络（RNN）及其变体中用于生成最终的类别预测。
3. 强化学习：在某些强化学习场景中，可用于将Q值（即动作的价值估计）转换为选择每个动作的概率，从而实现基于概率的动作选择策略。
4. 自然语言处理：用来计算注意力权重，这些权重决定了模型在处理输入时应该给予哪些部分更多的关注。

softmax函数是机器学习和深度学习中处理多分类问题、生成概率分布和进行概率决策的重要工具。

3. 两者的联系

最后，再分析下这两个函数的关系。
根据前面的介绍，sigmoid函数适合二分类问题，softmax函数适合多分类问题。
那么，sigmoid函数会不会是softmax函数的一个简化版本呢？

假设一个只有两个变量的softmax函数，那么其中\(y_0=\frac{e^{x_0}}{e^{x_0}+e^{x_1}}\)，
分子分母同时乘以\(e^{-x_0}\)可得：\(y_0=\frac{e^{x_0}e^{-x_0}}{e^{x_0}e^{-x_0}+e^{x_1}e^{-x_0}}=\frac{e^{x_0-x_0}}{e^{x_0-x_0}+e^{x_1-x_0}}=
\frac{1}{1+e^{-(x_0-x_1)}}\)
假设\(y=y_0, x = x_0-x_1\),可得：\(y=\frac{1}{1+e^{-x}}\)，
这就是一个典型的 sigmoid函数。

因此，我们可以认为softmax函数是将sigmoid函数扩展到多变量之后而得到的。