2023-10-11：用go语言，一个数字n，一定要分成k份， 得到的乘积尽量大是多少？ 数字n和k，可能非常大，到达10^12规模。 结果可能更大，所以返回结果对1000000007取模。 来自华为

2023-10-11：用go语言，一个数字n，一定要分成k份，

得到的乘积尽量大是多少？

数字n和k，可能非常大，到达10^12规模。

结果可能更大，所以返回结果对1000000007取模。

来自华为。

来自左程云。

答案2023-10-11：

大体过程如下：

算法1：暴力递归

1.首先判断k是否为0或者n是否小于k，若是则返回-1。

2.调用递归函数process1，传入参数n和k。

3.在递归函数中，若k为1，则返回n。

4.使用循环从1到rest（即剩余数字n）遍历cur，cur为当前需要划分的数字。

5.将cur与process1(rest-cur, j-1)相乘，得到当前划分下的乘积curAns。

6.若curAns大于ans，则更新ans为curAns。

7.返回ans作为结果。

算法2：贪心的解

1.首先判断k是否为0或者n是否小于k，若是则返回-1。

2.计算每份应得数字a，为n除以k的商。

3.计算有多少份应该升级成a+1，并将结果保存到变量b中。

4.初始化ans为1。

5.使用循环从0到b遍历i，将a+1乘以ans，更新ans的值。

6.使用循环从0到k-b遍历i，将a乘以ans，更新ans的值。

7.返回ans作为结果。

算法3：贪心的解（最优解）

1.首先判断k是否为0或者n是否小于k，若是则返回-1。

2.初始化变量mod为1000000007。

3.计算每份应得数字a，为n除以k的商。

4.计算有多少份应该升级成a+1，并将结果保存到变量b中。

5.调用函数power(a+1, b, mod)计算part1，表示a+1的b次方的结果对mod取模。

6.调用函数power(a, k-b, mod)计算part2，表示a的k-b次方的结果对mod取模。

7.返回(part1 * part2) % mod作为结果。

总的时间复杂度：

算法1：暴力递归的时间复杂度可以用递归树来表示，假设n和k的差值为m（即n-k=m），则递归树的高度为m，每个节点需要进行O(m)的计算，所以总的时间复杂度为O(m^m)。

算法2和算法3的时间复杂度为O(1)，因为只有常数次的运算。

总的空间复杂度：

算法1：暴力递归的空间复杂度为O(m)，递归树的高度为m，所以递归所需的栈空间为O(m)。

算法2和算法3的空间复杂度为O(1)，只需要常数个变量进行计算。

go完整代码如下：

package main

import "fmt"

// 暴力递归
// 一定能得到最优解
func maxValue1(n int, k int) int {
	if k == 0 || n < k {
		return -1
	}
	return process1(n, k)
}

// 剩余的数字rest，一定要拆成j份，返回最大乘积
func process1(rest int, j int) int {
	if j == 1 {
		return rest
	}
	// 10 , 3份
	// 1 * f(9,2)
	// 2 * f(8,2)
	// 3 * f(7,2)
	// ...
	ans := -1 << 31
	for cur := 1; cur <= rest && (rest-cur) >= (j-1); cur++ {
		curAns := cur * process1(rest-cur, j-1)
		if curAns > ans {
			ans = curAns
		}
	}
	return ans
}

// 贪心的解
// 这不是最优解，只是展示贪心思路
func maxValue2(n int, k int) int {
	if k == 0 || n < k {
		return -1
	}
	// 数字n，一定要分k份
	// 每份先得多少，n/k
	a := n / k
	// 有多少份可以升级成a+1
	b := n % k
	ans := 1
	for i := 0; i < b; i++ {
		ans *= a + 1
	}
	for i := 0; i < k-b; i++ {
		ans *= a
	}
	return ans
}

// 贪心的解
// 这是最优解
// 但是如果结果很大，让求余数...
func maxValue3(n int64, k int64) int {
	if k == 0 || n < k {
		return -1
	}
	mod := 1000000007
	a := n / k
	b := n % k
	part1 := power(a+1, b, mod)
	part2 := power(a, k-b, mod)
	return int((part1 * part2) % int64(mod))
}

// 返回a的n次方，%mod的结果
func power(a int64, n int64, mod int) int64 {
	ans := int64(1)
	tmp := a
	for n != 0 {
		if (n & 1) != 0 {
			ans = (ans * tmp) % int64(mod)
		}
		n >>= 1
		tmp = (tmp * tmp) % int64(mod)
	}
	return ans
}

func main() {
	// 可以自己来用参数实验
	n := 20
	k := 4
	fmt.Println(maxValue1(n, k))
	fmt.Println(maxValue2(n, k))
	// fmt.Println(maxValue3(n, k))
}

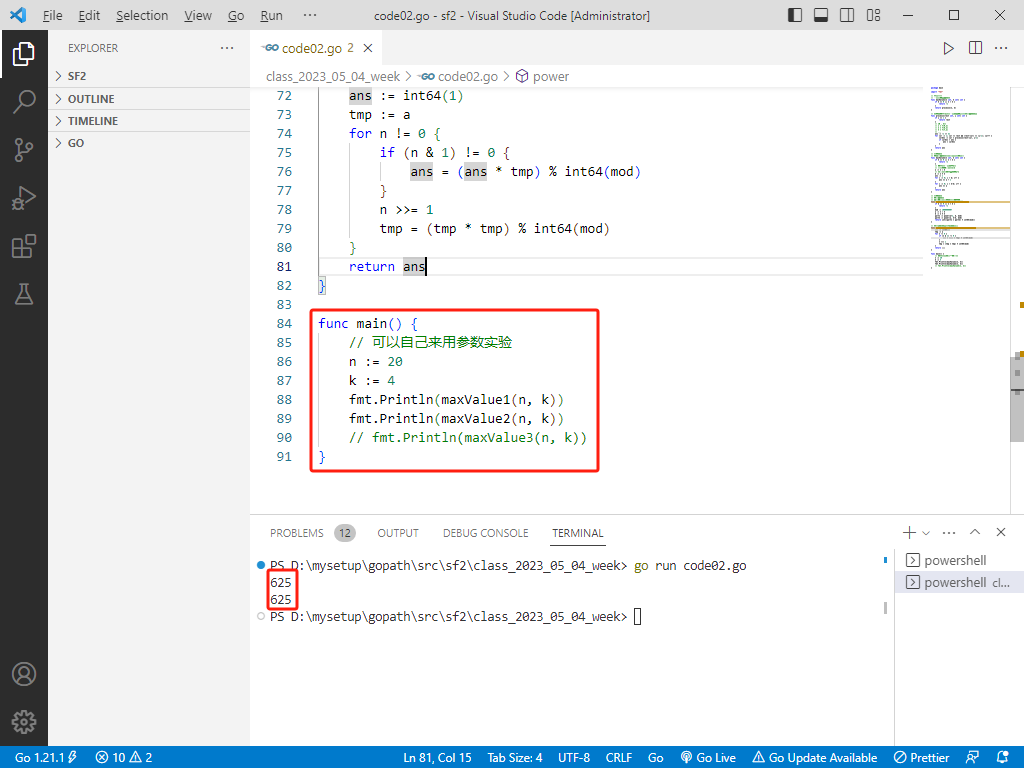
rust完整代码如下：

fn max_value1(n: i32, k: i32) -> i32 {
    if k == 0 || n < k {
        return -1;
    }
    process1(n, k)
}

fn process1(rest: i32, j: i32) -> i32 {
    if j == 1 {
        return rest;
    }
    let mut ans = i32::MIN;
    for cur in 1..=rest {
        if (rest - cur) >= (j - 1) {
            let cur_ans = cur * process1(rest - cur, j - 1);
            ans = ans.max(cur_ans);
        }
    }
    ans
}

fn max_value2(n: i32, k: i32) -> i32 {
    if k == 0 || n < k {
        return -1;
    }
    let a = n / k;
    let b = n % k;
    let mut ans = 1;
    for _ in 0..b {
        ans *= a + 1;
    }
    for _ in 0..(k - b) {
        ans *= a;
    }
    ans
}

fn max_value3(n: i64, k: i64) -> i32 {
    if k == 0 || n < k {
        return -1;
    }
    let mod_val = 1000000007;
    let a = n / k;
    let b = n % k;
    let part1 = power(a + 1, b, mod_val);
    let part2 = power(a, k - b, mod_val);
    (part1 * part2 % mod_val) as i32
}

fn power(a: i64, n: i64, mod_val: i64) -> i64 {
    let mut ans = 1;
    let mut tmp = a;
    let mut n = n;
    while n != 0 {
        if n & 1 != 0 {
            ans = ans * tmp % mod_val;
        }
        n >>= 1;
        tmp = tmp * tmp % mod_val;
    }
    ans
}

fn main() {
    let n = 20;
    let k = 4;
    println!("{}", max_value1(n, k));
    println!("{}", max_value2(n, k));
    println!("{}", max_value3(n as i64, k as i64));
}

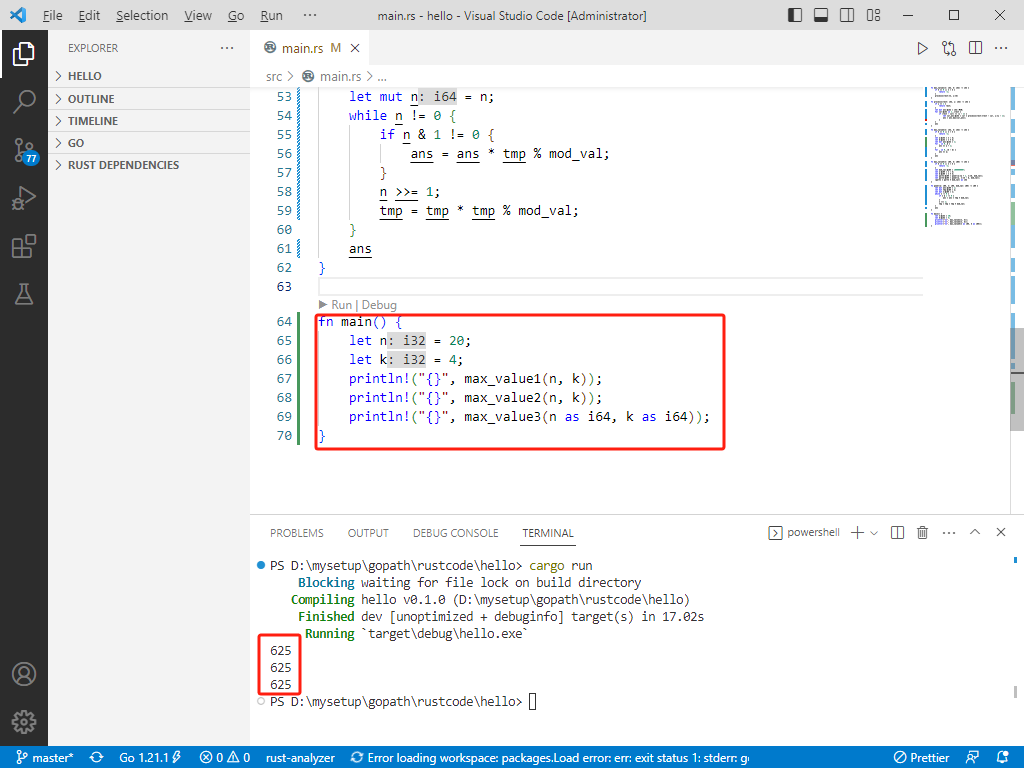
c++完整代码如下：

#include <iostream>
using namespace std;

int process1(int rest, int j)
{
    if (j == 1)
    {
        return rest;
    }
    int ans = INT_MIN;
    for (int cur = 1; cur <= rest && (rest - cur) >= (j - 1); cur++)
    {
        int curAns = cur * process1(rest - cur, j - 1);
        ans = max(ans, curAns);
    }
    return ans;
}

int maxValue1(int n, int k)
{
    if (k == 0 || n < k)
    {
        return -1;
    }
    return process1(n, k);
}

int maxValue2(int n, int k)
{
    if (k == 0 || n < k)
    {
        return -1;
    }
    int a = n / k;
    int b = n % k;
    int ans = 1;
    for (int i = 0; i < b; i++)
    {
        ans *= a + 1;
    }
    for (int i = 0; i < k - b; i++)
    {
        ans *= a;
    }
    return ans;
}

int power(long long a, long long n, int mod)
{
    long long ans = 1;
    long long tmp = a;
    while (n != 0) {
        if ((n & 1) != 0)
        {
            ans = (ans * tmp) % mod;
        }
        n >>= 1;
        tmp = (tmp * tmp) % mod;
    }
    return ans;
}

int maxValue3(long long n, long long k)
{
    if (k == 0 || n < k)
    {
        return -1;
    }
    int mod = 1000000007;
    long long a = n / k;
    long long b = n % k;
    long long part1 = power(a + 1, b, mod);
    long long part2 = power(a, k - b, mod);
    return (part1 * part2) % mod;
}

int main() {
    int n = 20;
    int k = 4;
    cout << maxValue1(n, k) << endl;
    cout << maxValue2(n, k) << endl;
    cout << maxValue3(n, k) << endl;
    return 0;
}

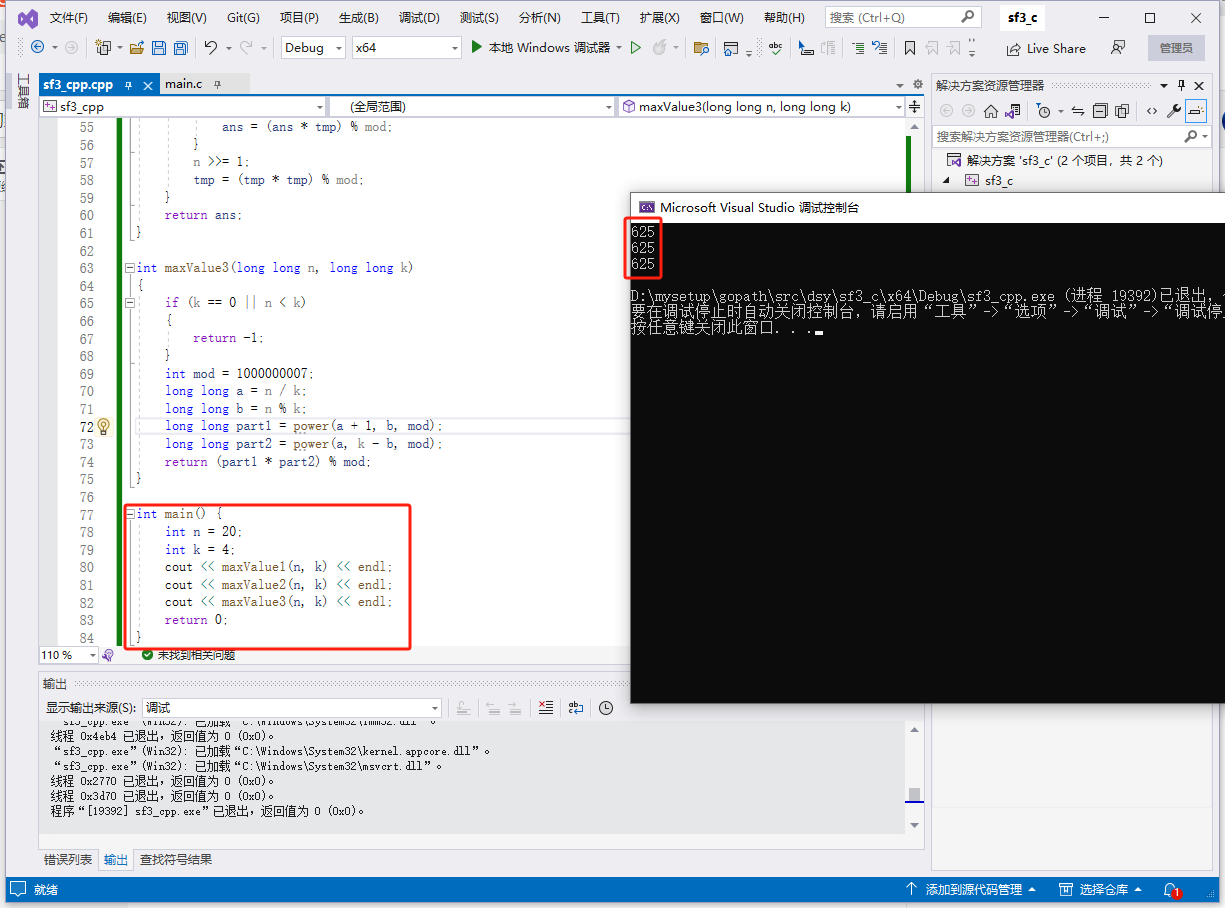
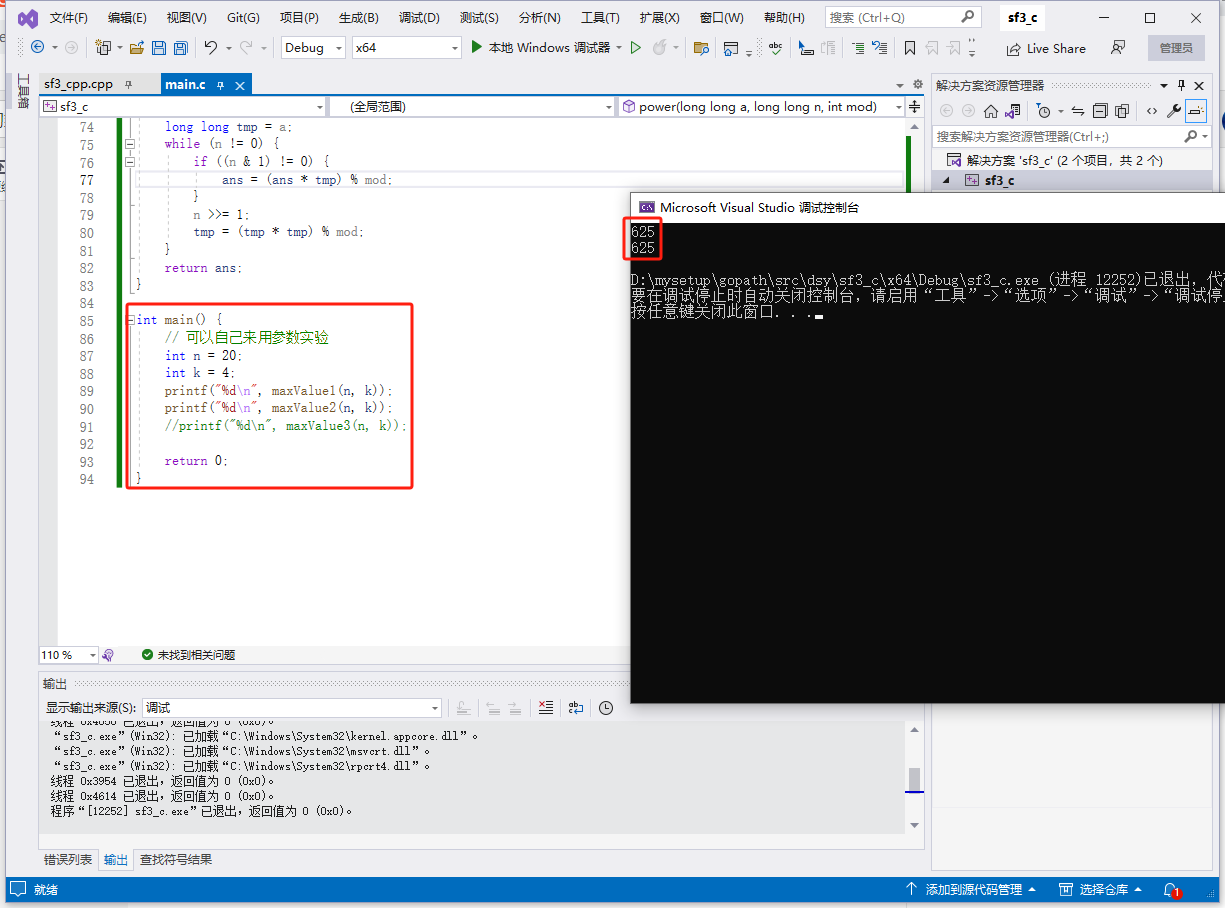
c完整代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 暴力递归
// 一定能得到最优解
int maxValue1(int n, int k) {
    if (k == 0 || n < k) {
        return -1;
    }
    return process1(n, k);
}

// 剩余的数字rest，一定要拆成j份，返回最大乘积
int process1(int rest, int j) {
    if (j == 1) {
        return rest;
    }
    // 10 , 3份
    // 1 * f(9,2)
    // 2 * f(8,2)
    // 3 * f(7,2)
    // ...
    int ans = -INT_MAX;
    for (int cur = 1; cur <= rest && (rest - cur) >= (j - 1); cur++) {
        int curAns = cur * process1(rest - cur, j - 1);
        if (curAns > ans) {
            ans = curAns;
        }
    }
    return ans;
}

// 贪心的解
// 这不是最优解，只是展示贪心思路
int maxValue2(int n, int k) {
    if (k == 0 || n < k) {
        return -1;
    }
    // 数字n，一定要分k份
    // 每份先得多少，n/k
    int a = n / k;
    // 有多少份可以升级成a+1
    int b = n % k;
    int ans = 1;
    for (int i = 0; i < b; i++) {
        ans *= a + 1;
    }
    for (int i = 0; i < k - b; i++) {
        ans *= a;
    }
    return ans;
}

long long power(long long a, long long n, int mod);

// 贪心的解
// 这是最优解
// 但是如果结果很大，让求余数...
int maxValue3(long long n, long long k) {
    if (k == 0 || n < k) {
        return -1;
    }
    int mod = 1000000007;
    long long a = n / k;
    long long b = n % k;
    long long part1 = power(a + 1, b, mod);
    long long part2 = power(a, k - b, mod);
    return (int)((part1 * part2) % mod);
}

// 返回a的n次方，%mod的结果
long long power(long long a, long long n, int mod) {
    long long ans = 1;
    long long tmp = a;
    while (n != 0) {
        if ((n & 1) != 0) {
            ans = (ans * tmp) % mod;
        }
        n >>= 1;
        tmp = (tmp * tmp) % mod;
    }
    return ans;
}

int main() {
    // 可以自己来用参数实验
    int n = 20;
    int k = 4;
    printf("%d\n", maxValue1(n, k));
    printf("%d\n", maxValue2(n, k));
    //printf("%d\n", maxValue3(n, k));

    return 0;
}