神经网络优化篇：详解Mini-batch 梯度下降（Mini-batch gradient descent）

Mini-batch 梯度下降

机器学习的应用是一个高度依赖经验的过程，伴随着大量迭代的过程，需要训练诸多模型，才能找到合适的那一个，所以，优化算法能够帮助快速训练模型。

其中一个难点在于，深度学习没有在大数据领域发挥最大的效果，可以利用一个巨大的数据集来训练神经网络，而在巨大的数据集基础上进行训练速度很慢。因此，会发现，使用快速的优化算法，使用好用的优化算法能够大大提高和团队的效率，那么，首先来谈谈mini-batch梯度下降法。

之前学过，向量化能够让有效地对所有\(m\)个样本进行计算，允许处理整个训练集，而无需某个明确的公式。所以要把训练样本放大巨大的矩阵\(X\)当中去，\(X= \lbrack x^{(1)}\ x^{(2)}\ x^{(3)}\ldots\ldots x^{(m)}\rbrack\)，\(Y\)也是如此，\(Y= \lbrack y^{(1)}\ y^{(2)}\ y^{(3)}\ldots \ldots y^{(m)}\rbrack\)，所以\(X\)的维数是\((n_{x},m)\)，\(Y\)的维数是\((1,m)\)，向量化能够让相对较快地处理所有\(m\)个样本。如果\(m\)很大的话，处理速度仍然缓慢。比如说，如果\(m\)是500万或5000万或者更大的一个数，在对整个训练集执行梯度下降法时，要做的是，必须处理整个训练集，然后才能进行一步梯度下降法，然后需要再重新处理500万个训练样本，才能进行下一步梯度下降法。所以如果在处理完整个500万个样本的训练集之前，先让梯度下降法处理一部分，算法速度会更快，准确地说，这是可以做的一些事情。

可以把训练集分割为小一点的子集训练，这些子集被取名为mini-batch，假设每一个子集中只有1000个样本，那么把其中的\(x^{(1)}\)到\(x^{(1000)}\)取出来，将其称为第一个子训练集，也叫做mini-batch，然后再取出接下来的1000个样本，从\(x^{(1001)}\)到\(x^{(2000)}\)，然后再取1000个样本，以此类推。

接下来要说一个新的符号，把\(x^{(1)}\)到\(x^{(1000)}\)称为\(X^{\{1\}}\)，\(x^{(1001)}\)到\(x^{(2000)}\)称为\(X^{\{2\}}\)，如果的训练样本一共有500万个，每个mini-batch都有1000个样本，也就是说，有5000个mini-batch，因为5000乘以1000就是5000万。

共有5000个mini-batch，所以最后得到是\(X^{\left\{ 5000 \right\}}\)

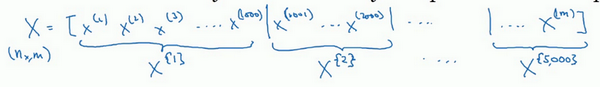
对\(Y\)也要进行相同处理，也要相应地拆分\(Y\)的训练集，所以这是\(Y^{\{1\}}\)，然后从\(y^{(1001)}\)到\(y^{(2000)}\)，这个叫\(Y^{\{2\}}\)，一直到\(Y^{\{ 5000\}}\)。

mini-batch的数量\(t\)组成了\(X^{\{ t\}}\)和\(Y^{\{t\}}\)，这就是1000个训练样本，包含相应的输入输出对。

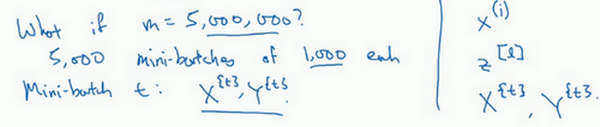
先确定一下的符号，之前使用了上角小括号\((i)\)表示训练集里的值，所以\(x^{(i)}\)是第\(i\)个训练样本。用了上角中括号\([l]\)来表示神经网络的层数，\(z^{\lbrack l\rbrack}\)表示神经网络中第\(l\)层的\(z\)值，现在引入了大括号\({t}\)来代表不同的mini-batch，所以有\(X^{\{ t\}}\)和\(Y^{\{ t\}}\)，检查一下自己是否理解无误。

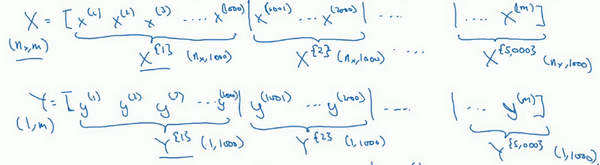
\(X^{\{ t\}}\)和\(Y^{\{ t\}}\)的维数：如果\(X^{\{1\}}\)是一个有1000个样本的训练集，或者说是1000个样本的\(x\)值，所以维数应该是\((n_{x},1000)\)，\(X^{\{2\}}\)的维数应该是\((n_{x},1000)\)，以此类推。因此所有的子集维数都是\((n_{x},1000)\)，而这些（\(Y^{\{ t\}}\)）的维数都是\((1,1000)\)。

解释一下这个算法的名称，batch梯度下降法指的是之前提过的梯度下降法算法，就是同时处理整个训练集，这个名字就是来源于能够同时看到整个batch训练集的样本被处理，这个名字不怎么样，但就是这样叫它。

相比之下，mini-batch梯度下降法，指的是在下面中会说到的算法，每次同时处理的单个的mini-batch \(X^{\{t\}}\)和\(Y^{\{ t\}}\)，而不是同时处理全部的\(X\)和\(Y\)训练集。

那么究竟mini-batch梯度下降法的原理是什么？在训练集上运行mini-batch梯度下降法，运行for t=1……5000，因为有5000个各有1000个样本的组，在for循环里要做得基本就是对\(X^{\{t\}}\)和\(Y^{\{t\}}\)执行一步梯度下降法。假设有一个拥有1000个样本的训练集，而且假设已经很熟悉一次性处理完的方法，要用向量化去几乎同时处理1000个样本。

首先对输入也就是\(X^{\{ t\}}\)，执行前向传播，然后执行\(z^{\lbrack 1\rbrack} =W^{\lbrack 1\rbrack}X + b^{\lbrack 1\rbrack}\)，之前这里只有，但是现在正在处理整个训练集，在处理第一个mini-batch，在处理mini-batch时它变成了\(X^{\{ t\}}\)，即\(z^{\lbrack 1\rbrack} = W^{\lbrack 1\rbrack}X^{\{ t\}} + b^{\lbrack1\rbrack}\)，然后执行\(A^{[1]k} =g^{[1]}(Z^{[1]})\)，之所以用大写的\(Z\)是因为这是一个向量内涵，以此类推，直到\(A^{\lbrack L\rbrack} = g^{\left\lbrack L \right\rbrack}(Z^{\lbrack L\rbrack})\)，这就是的预测值。注意这里需要用到一个向量化的执行命令，这个向量化的执行命令，一次性处理1000个而不是500万个样本。接下来要计算损失成本函数\(J\)，因为子集规模是1000，\(J= \frac{1}{1000}\sum_{i = 1}^{l}{L(\hat y^{(i)},y^{(i)})}\)，说明一下，这（\(L(\hat y^{(i)},y^{(i)})\)）指的是来自于mini-batch\(X^{\{ t\}}\)和\(Y^{\{t\}}\)中的样本。

如果用到了正则化，也可以使用正则化的术语，\(J =\frac{1}{1000}\sum_{i = 1}^{l}{L(\hat y^{(i)},y^{(i)})} +\frac{\lambda}{2 1000}\sum_{l}^{}{||w^{[l]}||}_{F}^{2}\)，因为这是一个mini-batch的损失，所以将\(J\)损失记为上角标\(t\)，放在大括号里（\(J^{\{t\}} = \frac{1}{1000}\sum_{i = 1}^{l}{L(\hat y^{(i)},y^{(i)})} +\frac{\lambda}{2 1000}\sum_{l}^{}{||w^{[l]}||}_{F}^{2}\)）。

也会注意到，做的一切似曾相识，其实跟之前执行梯度下降法如出一辙，除了现在的对象不是\(X\)，\(Y\)，而是\(X^{\{t\}}\)和\(Y^{\{ t\}}\)。接下来，执行反向传播来计算\(J^{\{t\}}\)的梯度，只是使用\(X^{\{ t\}}\)和\(Y^{\{t\}}\)，然后更新加权值，\(W\)实际上是\(W^{\lbrack l\rbrack}\)，更新为\(W^{[l]}:= W^{[l]} - adW^{[l]}\)，对\(b\)做相同处理，\(b^{[l]}:= b^{[l]} - adb^{[l]}\)。这是使用mini-batch梯度下降法训练样本的一步，写下的代码也可被称为进行“一代”（1 epoch）的训练。一代这个词意味着只是一次遍历了训练集。

使用batch梯度下降法，一次遍历训练集只能让做一个梯度下降，使用mini-batch梯度下降法，一次遍历训练集，能让做5000个梯度下降。当然正常来说想要多次遍历训练集，还需要为另一个while循环设置另一个for循环。所以可以一直处理遍历训练集，直到最后能收敛到一个合适的精度。

如果有一个丢失的训练集，mini-batch梯度下降法比batch梯度下降法运行地更快，所以几乎每个研习深度学习的人在训练巨大的数据集时都会用到。