Tarjan 学习笔记

萌新刚学Tarjan，啥也不会，肯定一堆错，请大佬指正谢谢

前置

强连通

• 强连通：

在不是强连通图的有向图\(G\)内，其顶点\(u\),\(v\)两个方向上都存在有向路径，则\(u\)和\(v\)强连通

• 强连通图：

对于有向图 \(G\) ，若\(G\)中任意两个结点连通，则称有向图\(G\)强连通。

• 强连通分量：

有向图的极大强连通子图

对于 \(G\) 的极大强连通子图 \(S\)，添加任意顶点都会导致 \(S\) 失去强连通的属性

桥

无向图中删除一条边会使这个图的极大联通分量数增加，这条边就是桥

桥一定是 dfs搜索树 中的边，并且一个简单环中的边一定都不是桥

• 判定法则：

对于时间戳\(dfn\)(在图的深度优先遍历中访问的顺序)

和追溯值\(low\)

(满足以下条件的节点的时间戳的最小值)

• \(x\) 的子树节点
• 通过不是搜索树的边可以到达 \(x\) 的子树节点的节点

满足\(\textit{dfn}[x]<\textit{low}[y]\)时，边 \((x,y)\) 是桥

一些变量

• \(\textit{dfn}_u\) ：深度优先搜索遍历时结点 \(u\) 被搜索的次序。

• \(\textit{low}_u\) ：在 \(u\) 的子树中能够回溯到的最早的已经在栈中的结点。设以 \(u\) 为根的子树为 \(\textit{Subtree}_u\) 。 \(\textit{low}_u\) 定义为以下结点的 \(\textit{dfn}\) 的最小值：

1. \(\textit{Subtree}_u\) 中的结点；
2. 从 \(\textit{Subtree}_u\) 通过一条不在搜索树上的边能到达的结点。

一个结点的子树内结点的 \(\textit{dfn}\) 都大于该结点的 \(\textit{dfn}\)。

从根开始的一条路径上的 \(\textit{dfn}\) 单调递增，\(\textit{low}\) 单调不下降。

DFS生成树

DFS生成树主要有\(4\)种边：

1. 树边：黑色边，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边
2. 反祖边：红色边（\(7 \rightarrow 1\) ）指向祖先结点的边
3. 横叉边：蓝色边（\(9 \rightarrow 7\)）在搜索的时候遇到了一个已经访问过的结点，这个结点并不是当前结点的祖先
4. 前向边：绿色边（\(3 \rightarrow 6\) ）搜索的时候遇到子树中的结点的时候形成的

若结点\(u\)是某个强连通分量在搜索树中遇到的第一个结点(就是根)，那么这个强连通分量的其余结点肯定是在DFS搜索树中以\(u\)为根的子树中。

正文

桥

我们可以看出，桥一定是dfs搜索树上的边而且一定不是一个简单环内的任何一个边

只要通过桥的判定法则直接求就行

注意事项

\(1\). 因为遍历的是无向图，所以无论从哪里都能遍历到这个节点的父节点\(fa\),所以不能用\(fa\)来更新\(low[x]\)

\(2\). 如果存在重边\(dfn[fa]\)就可以用来更新\(low[s]\),

解决方法：记录递归进入每个节点的编号，把无向图的每一条边都看做两条边成对存储

若沿着编号 \(i\) 的边递归进入节点 \(x\) , 则忽略从 \(x\) 出发的编号为 \(i\) xor \(1\) 的边，通过别的边更新 \(low[x]\)

Tarjan算法直接求出一张无向图的所有的桥，注意不能用 \(x\) 的父节点 \(fa\) 更新 \(low[x]\)

代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],n,m,tot,num;
bool bridge[maxm];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void tarjan(int x,int val){
    t[x].dfn=t[x].low=++num;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(!t[y].dfn){
            tarjan(y,i);
            t[x].low=min(t[x].low,t[y].low);
            if(t[y].low>t[x].dfn)
                bridge[i]=bridge[i^1]=1;
        }
        else if(i!=(val^1))
            t[x].low=min(t[x].low,t[y].dfn);
    }
}
signed main(){
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        add(x,y/*,z*/);
        add(y,x/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            tarjan(i,0);
    for(int i=2;i<tot;i+=2)
        if(bridge[i])
            cout<<t[i^1].ver<<" "<<t[i].ver<<endl;
}

割点

割点就是说删去节点 \(x\) 和所有和 \(x\) 关联的所有边后能够让无相图分裂成多个不相连的子图，节点 \(x\) 就是割点

割点判定定理：

若 \(x\) 不是搜索树的根节点，则当且仅当 \(x\) 的一个子节点 \(y\) 满足 \(dfn[x]\leq low[y]\)

若 \(x\) 是搜索树的根节点，则当且仅当搜索树上只要有两个节点 \(y_1,y_2\) 满足以上条件

代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],n,m,tot,num,root;
bool cut[maxm];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void tarjan(int x){
    t[x].dfn=t[x].low=++num;
    int f=0;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(!t[y].dfn){
            tarjan(y);
            t[x].low=min(t[x].low,t[y].low);
            if(t[y].low>=t[x].dfn){
                f++;
                if(x!=root||f>1)
                    cut[x]=1;
            }
        }
        else
            t[x].low=min(t[x].low,t[y].dfn);
    }
}
signed main(){
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        if(x==y) continue;
        add(x,y/*,z*/);
        add(y,x/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            root=i,
            tarjan(i);
    for(int i=1;i<=n;i++)
        if(cut[i])
            cout<<i<<endl;
}

双联通分量

介绍

如果一个无向图没有割点，那么称这个图为“点双连通图”，无向图的极大点双联通子图被称为「点双连通分量」，简称「v-DCC」

如果一个无向图没有桥，那么称这个图为“边双连通图”，无向图的极大边双联通子图被称为「边双联通分量」，简称「e-DCC」

两者合称「双联通分量」，简称「DCC」

定理

一张图是点双连通图，当且仅当满足两个条件之一

1.图的顶点数不超过\(2\)

2.图中任意两点都同时包含在至少一个简单环里

一张图是边双连通图，当且仅当任意一条边都包含在至少一个简单环里

边双连通分量

求法

先求出所有桥，然后全部删掉，分成的每个连通块都是一个边双联通分量

实现就是先用Tarjan标记所有的桥边，然后dfs划分出每个连通块

代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],n,m,tot,num,c[maxm],dcc;
bool bridge[maxm];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void tarjan(int x,int val){
    t[x].dfn=t[x].low=++num;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(!t[y].dfn){
            tarjan(y,i);
            t[x].low=min(t[x].low,t[y].low);
            if(t[y].low>t[x].dfn)
                bridge[i]=bridge[i^1]=1;
        }
        else if(i!=(val^1))
            t[x].low=min(t[x].low,t[y].dfn);
    }
}
void dfs(int x){
    c[x]=dcc;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(c[y]||bridge[i]) continue;
        dfs(y);
    }
}
signed main(){
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        add(x,y/*,z*/);
        add(y,x/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            tarjan(i,0);
    for(int i=1;i<=n;i++)
        if(!c[i])
            dcc++,
            dfs(i);
    cout<<dcc<<endl;//e-DCC的个数
    for(int i=1;i<=n;i++)
        cout<<i<<" "<<c[i]<<endl;//输出i属于第几个连通块
}

e-DCC的缩点

介绍

把每个e-DCC都看做一个节点，把桥边\((x,y)\)看做连接两个连通块，则会产生一棵树或一个森林，这就叫缩点

代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct HuaFengXiaYun{
    int ver,Next,edge;
}tree[maxm];
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],headc[maxm],tc,n,m,tot,num,c[maxm],dcc;
bool bridge[maxm];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void add_c(int x,int y){
    tree[++tc].ver=y;
    tree[tc].Next=headc[x];
    headc[x]=tc;
}
void tarjan(int x,int val){
    t[x].dfn=t[x].low=++num;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(!t[y].dfn){
            tarjan(y,i);
            t[x].low=min(t[x].low,t[y].low);
            if(t[y].low>t[x].dfn)
                bridge[i]=bridge[i^1]=1;
        }
        else if(i!=(val^1))
            t[x].low=min(t[x].low,t[y].dfn);
    }
}
void dfs(int x){
    c[x]=dcc;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;7
        if(c[y]||bridge[i]) continue;
        dfs(y);
    }
}
signed main(){
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        add(x,y/*,z*/);
        add(y,x/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            tarjan(i,0);
    for(int i=1;i<=n;i++)
        if(!c[i])
            dcc++,
            dfs(i);
    tc=1;
    for(int i=2;i<=tot;i++){
        int x=t[i^1].ver,y=t[i].ver;
        if(c[x]==c[y]) continue;
        add_c(c[x],c[y]);
    }
    cout<<dcc<<" "<< tc/2<<endl;//森林
    for(int i=2;i<tc;i+=2)
        cout<<tree[i^1].ver<<" "<<tree[i].ver<<endl;
}

点双联通分量

若一个节点没有其他边，那么这个节点自己构成一个v-DCC

除了孤立点，其他v-DCC的大小至少为2

并且一个割点不一定只属于一个v-DCC

求法

1. 当一个节点第一次被访问就入栈
2. 当割点判定法则成立时，无论 \(x\) 是否为根都要
   
   (1).一直弹出节点直到节点 \(y\) 被弹出
   
   (2).所有刚才弹出的节点和节点 \(x\) 构成一个v-DCC

代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct HuaFengXiaYun{
    int ver,Next,edge;
}tree[maxm];
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],n,m,tot,num,root,sta[maxm],top,cnt,new_id[maxm],tc,headc[maxm];
bool cut[maxm];
vector<int>dcc[maxn];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void add_c(int x,int y){
    tree[++tc].ver=y;
    tree[tc].Next=headc[x];
    headc[x]=tc;
}
void tarjan(int x){
    t[x].dfn=t[x].low=++num;
    sta[++top]=x;
    if(x==root&&head[x]==0){
        dcc[++cnt].push_back(x);
        return;
    }
    int f=0;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(!t[y].dfn){
            tarjan(y);
            t[x].low=min(t[x].low,t[y].low);
            if(t[y].low>=t[x].dfn){
                f++;
                if(x!=root||f>1)
                    cut[x]=1;
                cnt++;
                int z=0;
                while(z!=y){
                    z=sta[top--];
                    dcc[cnt].push_back(z);
                }
                dcc[cnt].push_back(x);
            }
        }
        else
            t[x].low=min(t[x].low,t[y].dfn);
    }
}
signed main(){
    freopen("1.in","r",stdin);
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        if(x==y) continue;
        add(x,y/*,z*/);
        add(y,x/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            root=i,
            tarjan(i);
    num=cnt;
    for(int i=1;i<=n;i++){
        if(cut[i])
            new_id[i]=++num;
    }
    tc=1;
    for(int i=1;i<=cnt;i++){
        for(int j=0;j<dcc[i].size();j++){
            int x=dcc[i][j];
            if(cut[x]){
                add_c(i,new_id[x]);
                add_c(new_id[x],i);
            }

        }
    }
    for(int i=1;i<=cnt;i++){
        cout<<i<<" ";
        for(int j=0;j<dcc[i].size();j++)
            cout<<dcc[i][j]<<" ";
        puts("");
    }
}

v-DCC的缩点

介绍

相比起e-DCC的缩点，v-DCC的缩点更复杂一些，因为一个割点可能属于多个v-DCC

若图中有 \(n\) 个割点和 \(m\) 个v-DCC，那么要建立一个有 \(n+m\) 个节点的新图

连边之后可以发现这个新的图是一棵树或者森林

代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct HuaFengXiaYun{
    int ver,Next,edge;
}tree[maxm];
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],n,m,tot,num,root,sta[maxm],top,cnt,new_id[maxm],tc,headc[maxm];
bool cut[maxm];
vector<int>dcc[maxn];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void add_c(int x,int y){
    tree[++tc].ver=y;
    tree[tc].Next=headc[x];
    headc[x]=tc;
}
void tarjan(int x){
    t[x].dfn=t[x].low=++num;
    sta[++top]=x;
    if(x==root&&head[x]==0){
        dcc[++cnt].push_back(x);
        return;
    }
    int f=0;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(!t[y].dfn){
            tarjan(y);
            t[x].low=min(t[x].low,t[y].low);
            if(t[y].low>=t[x].dfn){
                f++;
                if(x!=root||f>1)
                    cut[x]=1;
                cnt++;
                int z=0;
                while(z!=y){
                    z=sta[top--];
                    dcc[cnt].push_back(z);
                }
                dcc[cnt].push_back(x);
            }
        }
        else
            t[x].low=min(t[x].low,t[y].dfn);
    }
}
signed main(){
    freopen("1.in","r",stdin);
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        if(x==y) continue;
        add(x,y/*,z*/);
        add(y,x/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            root=i,
            tarjan(i);
    num=cnt;
    for(int i=1;i<=n;i++){
        if(cut[i])
            new_id[i]=++num;
    }
    tc=1;
    for(int i=1;i<=cnt;i++){
        for(int j=0;j<dcc[i].size();j++){
            int x=dcc[i][j];
            if(cut[x]){
                add_c(i,new_id[x]);
                add_c(new_id[x],i);
            }

        }
    }
    cout<<num<<" "<<tc/2<<endl;//点数，边数
    for(int i=2;i<tc;i+=2)
        cout<<tree[i^1].ver<<" "<<tree[i].ver<<endl;
}

强连通分量

简写SCC

追溯值：

这里的追溯值和无向图的不同，\(x\) 的追溯值 \(low[x]\) 定义为满足以下条件的节点的最小时间戳

1. 该点在栈中
2. 存在一条从\(x\)的子树出发的有向边,以该点为终点

算法

按照 dfs 序对所有结点进行搜索，维护每个点的 \(\textit{dfn}\) 与 \(\textit{low}\) ，让搜索到的结点入栈。每找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。搜索过程中，对于结点 \(u\) 和与其相邻的结点 \(v\)(\(v\) 不是 \(u\) 的父节点)进行分类讨论：

• \(v\) 未被访问：继续对 \(v\) 进行dfs。在回溯过程中，用 \(\textit{low}_v\) 更新 \(\textit{low}_u\) 。因为存在从 \(u\) 到 \(v\) 的直接路径，所以 \(v\) 能够回溯到的已经在栈中的结点， \(u\) 也一定能够回溯到。

• \(v\) 被访问过，在栈中：根据 low 值的定义，用 \(\textit{dfn}_v\) 更新 \(\textit{low}_u\) 。

• \(v\) 被访问过，不在栈中：说明 \(v\) 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

判定法则

若\(x\)回溯前,\(low[x]=dfn[x]\)成立则从栈中从\(x\)到栈顶的所有节点构成一个SCC

代码

vector数组scc中scc[i]记录编号为 \(i\) 的SCC中所有节点

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],n,m,tot,num,f,root,sta[maxm],top,cnt,ins[maxm];
bool cut[maxm];
vector<int>scc[maxm];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void tarjan(int x){
    t[x].dfn=t[x].low=++num;
    sta[++top]=x;
    ins[x]=1;
    for(int i=head[x];i;i=t[i].Next){
        if(!t[t[i].ver].dfn){
            tarjan(t[i].ver);
            t[x].low=min(t[x].low,t[t[i].ver].low);
        }
        else
            t[x].low=min(t[x].low,t[t[i].ver].dfn);
    }
    if(t[x].dfn==t[x].low){
        cnt++;
        int y;
        while(x!=y){
            y=sta[top--],ins[y]=0;
            c[y]=cnt,scc[cnt].push_back(y);
        }
    }
}
signed main(){
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        if(x==y) continue;
        add(x,y/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            tarjan(i);
    for(int i=1;i<=cnt;i++){
        cout<<i<<" ";
        for(int j=0;j<=scc[i].size();j++)
            cout<<scc[i][j]<<" ";
        puts("");
    }
}

缩点

类似无向图的e-DCC，每个SCC也可以缩成一个点

方法

对于每条有向边\((x,y)\)，若\(\ c[x]\ 不等于\ c[y]\) 则在编号为\(c[x]\)和\(c[y]\)的SCC之间连边，最后可以得到一个有向无环图

代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct HuaFengXiaYun{
    int ver,Next,edge;
}tree[maxm];
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],tc,headc[maxm],n,m,tot,num,f,root,sta[maxm],top,cnt,ins[maxm],c[maxm];
bool cut[maxm];
vector<int>scc[maxm];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void add_c(int x,int y){
    tree[++tc].ver=y;
    tree[tc].Next=headc[x];
    headx[x]=tc;
}
void tarjan(int x){
    t[x].dfn=t[x].low=++num;
    sta[++top]=x;
    ins[x]=1;
    for(int i=head[x];i;i=t[i].Next){
        if(!t[t[i].ver].dfn){
            tarjan(t[i].ver);
            t[x].low=min(t[x].low,t[t[i].ver].low);
        }
        else
            t[x].low=min(t[x].low,t[t[i].ver].dfn);
    }
    if(t[x].dfn==t[x].low){
        cnt++;
        int y;
        while(x!=y){
            y=sta[top--],ins[y]=0;
            c[y]=cnt,scc[cnt].push_back(y);
        }
    }
}
signed main(){
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        if(x==y) continue;
        add(x,y/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            tarjan(i);
    for(int x=1;x<=n;x++){
        for(int i=head[x];i;i=t[i].Next){
            int y=t[i].ver;
            if(c[x]==c[y]) continue;
            add_c(c[x],c[y]);
        }
    }
}

有向图的必经点和必经边

给定一张起点为\(S\),终点为\(T\)的有向图，若从\(S\)到\(T\)的每条路径一定会经过一个节点\(x\)那么这个点被称作必经点

同理，一定会经过一条边\((x,y)\)那么这条边就是必经边或桥

环上的点也可能是必经点,环上的边也可能是必经边,所以不能简单的缩点然后求解DAG

方法一 Lenguar-Tarjan算法

计算支配树然后在\(O(n\log n)\)时间内求解

那么什么是支配树呢？

给定一个有向图和一个起点\(S\),若去掉其中某个节点\(x\)无法到达终点\(P\)，则称节点\(x\)支配点\(P\)，\(x\)是\(p\)的一个支配点

支配点\(x\)可以有多个,这个集合称为\({X_p}\)，最少有两个支配点，一个是起点，一个是终点

甚至支配点有传递的性质

a 是 b 的支配点，c 是 b 的支配点，那么必定存在 (a是b的支配点)|| (b是a的支配点)

这是一个有向图

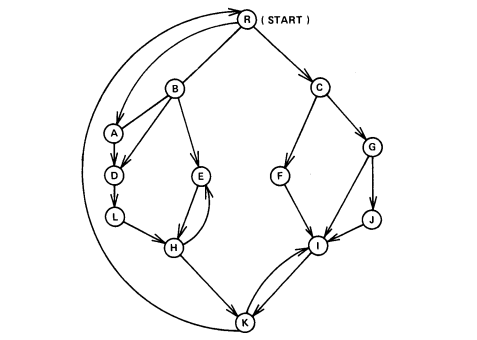
说到底什么是支配树呢？

在支配\(p\)的点中，若一个支配点\(i≠p\)，满足\(i\)被\(p\)剩下的所有支配点支配，则称\(i\)为\(p\)的最近支配点

把图的根节点记作\(root\)，除了\(root\)以外的每一点都存在唯一的最近支配点，连上所有\((x的最近支配点,x)\)的边就能得到一颗树

这棵树被称作支配树

这是一颗支配树

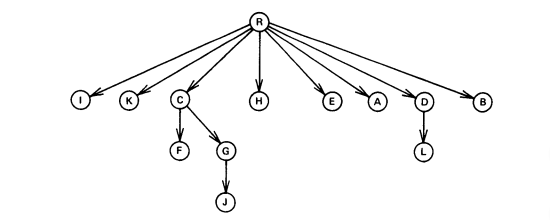
那么怎么实现呢？

我们成功发现，支配树也太难了，建议使用方法2

方法二 (比较简单)

1. 在原图中拓扑序进行DP求出路径条数\(f[x]\)
2. 在反图中拓扑序进行DP求出路径条数\(dp[x]\)

其中\(f[T]\)为\(S\)到\(T\)的路径总条数

对于有向边\((x,y)\)，若\(f[x]\times dp[y]=f[T]\)则\((x,y)\)为从\(S\)到\(T\)的必经边

对于点\(x\)，若\(f[x]\times dp[x]=f[T]\)则\(x\)为从\(S\)到\(T\)的必经点

这个一般会超long long,可以对一个大质数取模再保存到\(f\)和\(dp\)数组里

然后可能会误判，只要不卡常可以多模几个质数再计算

代码

咕咕咕

2-SAT问题

例题

1. 受欢迎的牛

洛谷P不知道多少，普及组OJ

• 题面

每一头牛的愿望就是变成一头最受欢迎的牛。

现在有\(N\)头牛，给你\(M\)对整数\((A,B)\)，表示牛\(A\)认为牛\(B\)受欢迎。

这种关系是具有传递性的，如果\(A\)认为\(B\)受欢迎，\(B\)认为\(C\)受欢迎，那么牛\(A\)也认为牛\(C\)受欢迎。

你的任务是求出有多少头牛被所有的牛认为是受欢迎的。

• 思路：

Tarjan缩点板子题稍微改动，思路就是先跑有向图的Tarjan，然后统计出度

缩点后找出度为 \(0\) 的点个数

如果个数\(>1\)则不存在受欢迎的牛(因为如果有出度那么对方就不喜欢自己，不然就缩成一个点了)

如果个数\(=0\)那么这个图不是DAG图，明显不可能这都缩完了啊怎么会

如果个数\(=1\)直接输出这个强连通分量里的节点数

• 评价

不难，但是听说很经典

点击启动原神

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct HuaFengXiaYun{
    int ver,Next,edge;
}tree[maxm];
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],out[maxm],tc,headc[maxm],n,m,tot,num,f,summ[maxm],sum,sta[maxm],top,cnt,ins[maxm],c[maxm],genshin[maxm];
bool cut[maxm];
vector<int>scc[0x66cc];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void add_c(int x,int y){
    tree[++tc].ver=y;
    tree[tc].Next=headc[x];
    headc[x]=tc;
}
void tarjan(int x){
    t[x].dfn=t[x].low=++num;
    sta[++top]=x;
    ins[x]=1;
    for(int i=head[x];i;i=t[i].Next){
        if(!t[t[i].ver].dfn){
            tarjan(t[i].ver);
            t[x].low=min(t[x].low,t[t[i].ver].low);
        }
        else
            t[x].low=min(t[x].low,t[t[i].ver].dfn);
    }
    if(t[x].dfn==t[x].low){
        cnt++;
        int y;
        while(x!=y){
            y=sta[top--],
            ins[y]=0;
            c[y]=cnt,
            scc[cnt].push_back(y);
        }
    }
}
signed main(){
    n=read(),m=read();
    tot=1;
    for(int i=1;i<=m;i++){
        int x=read(),y=read()/*,z=read()*/;
        if(x==y) continue;
        add(x,y/*,z*/);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            tarjan(i);
    for(int x=1;x<=n;x++){
        for(int i=head[x];i;i=t[i].Next){
            int y=t[i].ver;
            if(c[x]==c[y]) continue;
            add_c(c[x],c[y]);
            sum++;
        }
    }
    for(int i=headc[1];i;i=tree[i].Next){
        summ[i]++;
    }
    int abc=0,ans=0;
    for(int i=1;i<=cnt;i++){
        if(summ[i]==0)
            abc++,
            ans+=scc[i].size();
    }
    cout<<ans;
}

2.备用交换机

点击查看代码

#include<bits/stdc++.h>
#define lC q<<1
#define rC q<<1|1
#define int long long
#define INF 0x66ccff0712
#define endl "\n"
#define maxm 0x66ccff
#define maxn 0x6cf
#define mid ((l+r)>>1)
#define void inline void
using namespace std;
inline int read(){
    int s = 0,w = 1;char ch = getchar();
    while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}
    while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}
    return s*w;
}
struct LuoShuiTianYi{
    int ver,Next,edge,dfn,low;
}t[maxm];
int head[maxm],n,m,tot,num,root,sum;
bool cut[maxm];
void add(int x,int y/*,int z*/){
    t[++tot].ver=y;
    // t[tot].edge=z;
    t[tot].Next=head[x];
    head[x]=tot;
}
void tarjan(int x){
    t[x].dfn=t[x].low=++num;
    int f=0;
    for(int i=head[x];i;i=t[i].Next){
        int y=t[i].ver;
        if(!t[y].dfn){
            tarjan(y);
            t[x].low=min(t[x].low,t[y].low);
            if(t[y].low>=t[x].dfn){
                f++;
                if(x!=root||f>1)
                    cut[x]=1;
            }

        }
        else
            t[x].low=min(t[x].low,t[y].dfn);
    }
}
signed main(){
    n=read();
    int x,y;
    tot=1;
    while(cin>>x>>y){
        if(x==y) continue;
        add(x,y);
        add(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!t[i].dfn)
            root=i,
            tarjan(i);
    for(int i=1;i<=n;i++)
        if(cut[i]){
            sum++;
        }
    cout<<sum<<endl;
    for(int i=1;i<=n;i++)
        if(cut[i]){
            cout<<i<<endl;
        }

}

完结撒花