论文解读（ECACL）《ECACL: A Holistic Framework for Semi-Supervised Domain Adaptation》

Note：[ wechat：Y466551 | 付费咨询，非诚勿扰 ]

论文信息

论文标题：ECACL: A Holistic Framework for Semi-Supervised Domain Adaptation
论文作者：Kai Li, Chang Liu, Handong Zhao, Yulun Zhang, Y. Fu
论文来源：2021 ICCV
论文地址：download 
论文代码：download
视屏讲解：click

1 介绍

　　出发点：半监督领域自适应（SSDA）是一个实用但尚未被研究的研究课题；

2 方法

2.1 模型框架

　　

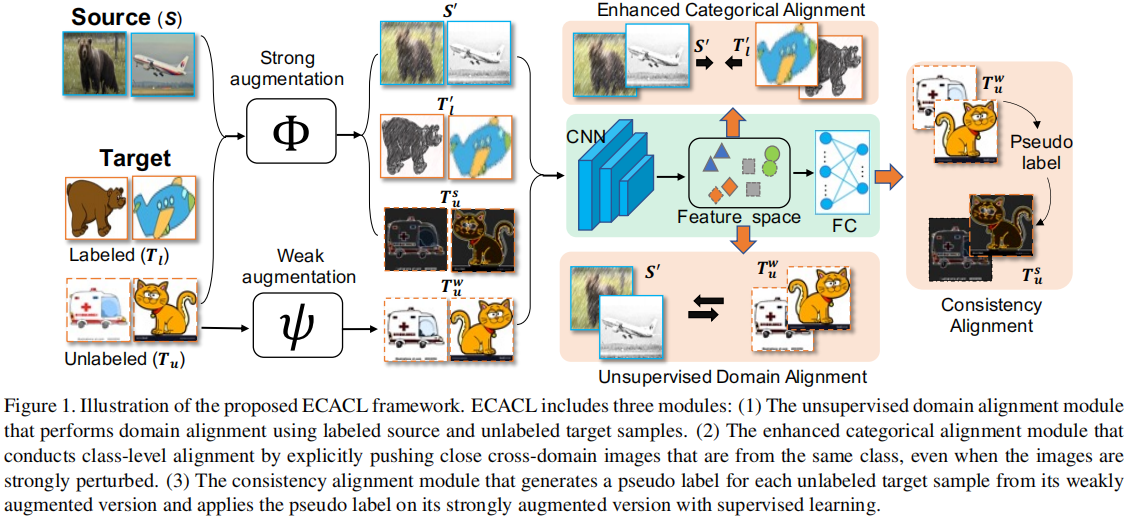
2.2 类对齐

基于原型损失的方法

　　使用目标域带标记数据计算原型：

　　　　$\mathbf{c}_{k}=\frac{1}{\left|\mathcal{T}_{k}\right|} \sum_{\left(\mathbf{t}_{i}, y_{i}\right) \in \mathcal{T}_{k}} f\left(\mathbf{t}_{i}\right)  \quad\quad(1)$

　　使用上述得到的目标原型，计算源域样本原型分布：

　　　　$p\left(y_{i}^{s}=y \mid \mathbf{s}_{i}\right)=\frac{\exp \left(-\left\|f\left(\mathbf{s}_{i}\right)-\mathbf{c}_{y}\right\|_{2}\right)}{\sum_{k=1}^{C} \exp \left(-\left\|f\left(\mathbf{s}_{i}\right)-\mathbf{c}_{k}\right\|_{2}\right)}\quad\quad(2)$

　　然后，可计算出所有源样本的原型损失：

　　　　$L_{p a}=\frac{1}{C N_{s}} \sum_{\left(\mathbf{s}_{i}, y_{i}^{s}\right) \sim \mathcal{S}} \sum_{y \sim \mathcal{Y}} y_{i}^{s} \log \left[-p\left(y_{i}^{s}=y \mid \mathbf{s}_{i}\right)\right] \quad\quad(3)$

基于三重损失的方法

　　目的：使同一类的跨域样本应该比来自不同类[16]的样本具有更高的相似性。

　　具体来说，对于目标域带标记样本 $\left(\mathbf{t}_{i}, y_{i}^{t}\right) \in \mathcal{T}_{l}$，从 $\mathcal{S}$ 中发现属于 $y_t$ 类，但最不相似的源样本 $\left(\mathbf{s}_{p}, y_{p}\right)$。同时，也从 $\mathcal{S}$ 中找到不属于 $y_t$ 类，但最相似的样本 $\left(\mathbf{s}_{n}, y_{n}\right)$。三联体 $\left(\mathbf{t}_{i}, \mathbf{s}_{n}, \mathbf{s}_{p}\right)$，将以下三联体损失优化为：

　　　　$\begin{aligned}L_{t a}= & \frac{1}{N_{t}} \sum_{\left(\mathbf{t}_{i}, y_{t}\right) \sim \mathcal{T}_{l}}\left[\left\|f\left(\mathbf{t}_{i}\right)-f\left(\mathbf{s}_{p}\right)\right\|_{2}^{2}-\right.\left.\left\|f\left(\mathbf{t}_{i}\right)-f\left(\mathbf{s}_{n}\right)\right\|_{2}^{2}+m\right]_{+} \end{aligned}\quad\quad(4)$

2.3 域对齐与数据增强

增强的类对齐

　　最近的研究表明，创建高度扰动图像的强增强为监督学习[6,7]带来了显著的性能提高。因此，$\text{Eq.1-4}$ 均基于随机强数据增强样本计算得出。

一致性对齐

　　对于每个未标记的目标样本 $\mathbf{u}_{i} \in \mathcal{T}_{u}$，应用弱增强 $\psi$ 和强增强 $\Phi$:

　　　　$\begin{aligned}\mathbf{u}_{i}^{w} & =\psi\left(\mathbf{u}_{i}\right)\\\mathbf{u}_{i}^{s} & =\Phi\left(\mathbf{u}_{i}\right)\end{aligned}\quad\quad(5)$

　　优化以下目标函数:

　　　　$L_{\text {cona }}=\sum_{\mathbf{u}_{i} \sim \mathcal{U}}\left[\mathbb{1}\left(\max \left(\mathbf{p}_{w}\right) \geq \sigma\right) H\left(\tilde{\mathbf{p}}_{w}, \mathbf{p}_{s}\right)\right]\quad\quad(6)$

　　其中，$\tilde{\mathbf{p}}_{w}=   \arg \max \left(\mathbf{p}_{w}\right) $，$H(., . )$ 代表着交叉熵；

2.4 训练目标

　　总体学习目标是 UDA损失、增强的类对齐损失和一致性对齐损失的加权组合：

　　　　$L=L_{\text {uda }}+\lambda_{1} L_{\text {cata }}+\lambda_{2} L_{\text {cona }}, \quad L_{\text {cata }}=\left\{L_{p a}^{\prime}, L_{\text {ta }}^{\prime}\right\}$

　　其中，$L_{c a t a}=L_{p a}^{\prime}$ 或者 $L_{\text {cata }}=L_{t a}^{\prime} $；

　　算法：

　　　　

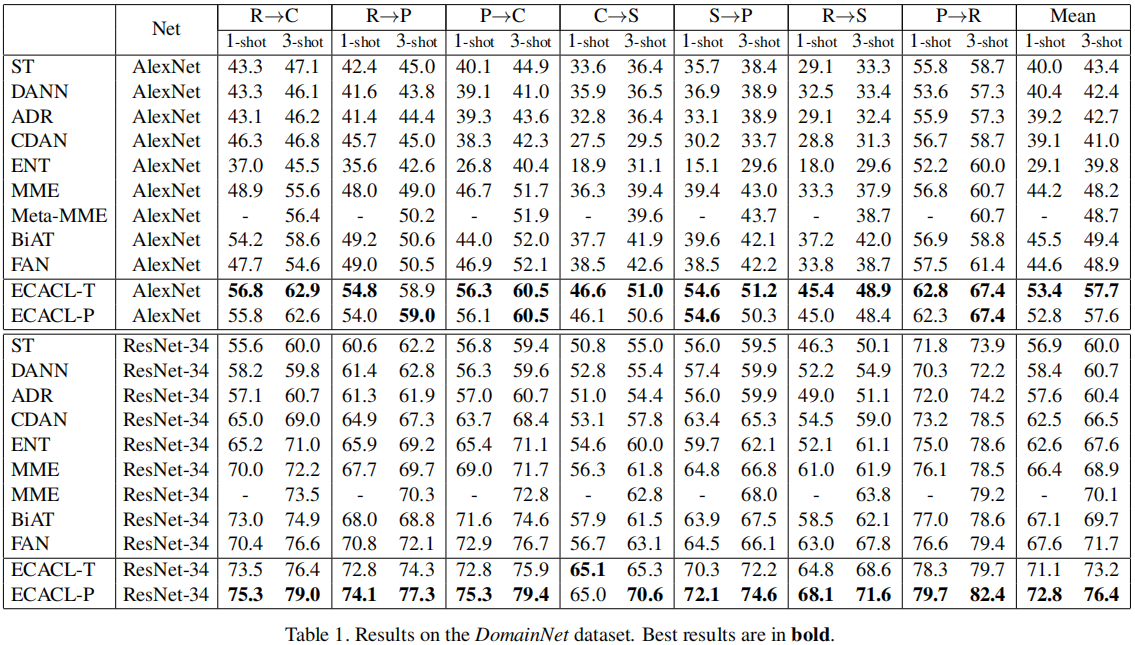
3 实验

分类