【luoguP1196】 [NOI2002]银河英雄传说--边带权并查集 ，

题目描述

公元五八○一年，地球居民迁至金牛座α第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历七九九年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成3000030000列，每列依次编号为1, 2, …,300001,2,…,30000。之后，他把自己的战舰也依次编号为1, 2, …, 300001,2,…,30000，让第ii号战舰处于第ii列(i = 1, 2, …, 30000)(i=1,2,…,30000)，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为M_{i,j}Mi,j​，含义为第i号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：C_{i,j}Ci,j​。该指令意思是，询问电脑，杨威利的第ii号战舰与第jj号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

最终的决战已经展开，银河的历史又翻过了一页……

输入格式

第一行有一个整数T(1 \le T \le 500,000)T(1≤T≤500,000)，表示总共有TT条指令。

以下有TT行，每行有一条指令。指令有两种格式：

1. M_{i,j}Mi,j​ ：ii和jj是两个整数(1 \le i,j \le 30000)(1≤i,j≤30000)，表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第ii号战舰与第jj号战舰不在同一列。

2. C_{i,j}Ci,j​ ：ii和jj是两个整数(1 \le i,j \le 30000)(1≤i,j≤30000)，表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出格式

依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第ii号战舰与第jj号战舰之间布置的战舰数目。如果第ii号战舰与第jj号战舰当前不在同一列上，则输出-1−1。

输入输出样例

输入 #1复制

4
M 2 3
C 1 2
M 2 4
C 4 2

输出 #1复制

-1
1

说明/提示

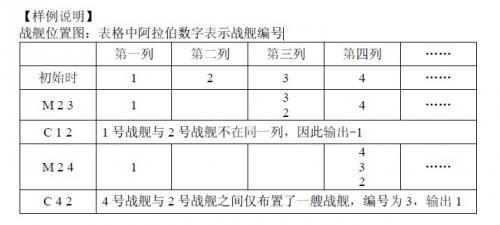
【样例说明】

战舰位置图：表格中阿拉伯数字表示战舰编号

思路：

　　边带权并查集，附加维护两个数组，dis存的是不包括该节点的祖先节点数，初始值为0，siz表示以他为根的字树的size，注意这里的字符读入是scanf 里是%s,不能是

%c,因为可能有空格或回车，也可以开个数组，用%s

并查集：

int find(int x)
{
	if(fa[x]!=x)
	{
		int f=find(fa[x]);
		dis[x]+=dis[fa[x]];
		fa[x]=f;
	}
	return fa[x];
}

修改操作：

if(ch=='M')
		{
			fa[fx]=fy;
			dis[fx]=siz[fy];
			siz[fy]+=siz[fx];
		}
		else
		{
			if(fx!=fy)printf("-1\n");
			else printf("%d\n",abs(dis[x]-dis[y])-1);
		}

代码：

#include<cstdio>
#include<iostream>
#include<cstdlib>
using namespace std;
const int N = 35000;
int T,fa[N],dis[N],siz[N];
char ch;
int find(int x)
{
	if(fa[x]!=x)
	{
		int f=find(fa[x]);
		dis[x]+=dis[fa[x]];
		fa[x]=f;
	}
	return fa[x];
}
int main()
{
	for(int i=1;i<=30000;i++)fa[i]=i,siz[i]=1;
	scanf("%d",&T);
	int x,y;
	while(T--)
	{
		scanf("%s%d%d",&ch,&x,&y);
		int fx=find(x),fy=find(y);
		if(ch=='M')
		{
			fa[fx]=fy;
			dis[fx]=siz[fy];
			siz[fy]+=siz[fx];
		}
		else
		{
			if(fx!=fy)printf("-1\n");
			else printf("%d\n",abs(dis[x]-dis[y])-1);
		}
	}
	return 0;
}